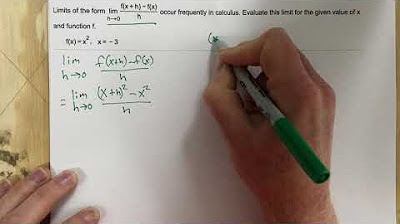2.2 - Problem #10 (Calc)
TLDRThis video script walks through the process of evaluating a limit related to the concept of secant lines, tangents, and instantaneous rates in calculus. The function given is f(x) = √x, and the task is to find the slope of the tangent line at x = 7. The solution involves manipulating the limit expression by multiplying the conjugate to simplify, then evaluating the limit as h approaches zero. The final result is the derivative of the function at x = 7, which is 1/(2√7), and the script also explains how to rationalize the denominator for clarity.
Takeaways
- 📚 The problem involves evaluating a limit related to secant lines, tangents, and instantaneous rates in calculus.
- 🔍 The given function is f(x) = √x, and the limit is to be evaluated at x = 7.
- 📘 The limit to evaluate is the derivative form: lim(h->0) [f(x+h) - f(x)] / h.
- 🤔 The initial step is to substitute x+h into the function and simplify the expression before taking the limit.
- 🧩 The process involves multiplying the numerator and denominator by the conjugate to simplify the square root expression.
- 🔄 After simplification, the limit simplifies to 1 / (√(x + h) + √x).
- 📉 The limit is then evaluated as h approaches 0, which results in 1 / (2√x).
- 🔢 Substituting x = 7 into the simplified limit formula gives the slope of the tangent line at that point.
- 📌 The slope, or derivative, at x = 7 is 1 / (2√7).
- 📝 There's a mention of rationalizing the denominator, resulting in two possible representations of the slope: 1 / (2√7) and √7 / 14.
- 📑 The transcript provides a step-by-step walkthrough of the calculus problem-solving process, including simplification and rationalization.
Q & A
What is the main objective of the problem discussed in the transcript?
-The main objective of the problem is to evaluate the limit of the form \( \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \) for the given function \( f(x) = \sqrt{x} \) at \( x = 7 \), which represents the slope of the tangent line to the curve at that point.
What is the given function in the problem?
-The given function is \( f(x) = \sqrt{x} \), which is the square root of x.
Why can't the value of h be substituted with zero directly in the limit?
-The value of h cannot be substituted with zero directly because it would result in a division by zero, which is undefined.
What mathematical technique is used to avoid division by zero in this context?
-The technique used is conjugate multiplication to eliminate the root expression in the numerator and denominator without actually dividing by zero.
What does the expression \( \frac{\sqrt{x+h} + \sqrt{x}}{\sqrt{x+h} - \sqrt{x}} \) simplify to?
-After simplifying, the expression becomes \( \frac{2\sqrt{x}}{\sqrt{x+h} + \sqrt{x}} \), which is derived from the conjugate multiplication technique.
What happens when h approaches zero in the simplified expression?
-As h approaches zero, the expression simplifies to \( \frac{1}{2\sqrt{x}} \) because the h terms cancel out.
What is the final expression for the limit after rationalizing the denominator?
-The final expression for the limit, after rationalizing the denominator, is \( \frac{\sqrt{7}}{7} \) or \( \frac{7\sqrt{7}}{49} \) with a rationalized denominator.
What is the slope of the tangent line to the curve at x = 7?
-The slope of the tangent line to the curve at x = 7 is \( \frac{\sqrt{7}}{7} \) or \( \frac{7\sqrt{7}}{49} \) after rationalizing the denominator.
Why is it necessary to rationalize the denominator in the final answer?
-Rationalizing the denominator is necessary to eliminate any radicals in the denominator, which is a common practice to express the answer in its simplest form.
What does the process of evaluating this limit represent in the context of calculus?
-Evaluating this limit represents finding the instantaneous rate of change of the function at a particular point, which is the definition of the derivative in calculus.
How does the process described in the transcript relate to the concept of secant lines and tangents?
-The process relates to secant lines and tangents as it involves finding the slope of a line that just touches the curve at a point, which is the definition of a tangent, and the limit of the slopes of secant lines as they approach the tangent line.
Outlines
📚 Calculus Limit Problem with Root Function
The script discusses a calculus problem involving the limit of a function related to secant lines, tangents, and instantaneous rates. The function given is f(x) = √x, and the task is to evaluate the limit as h approaches zero of (f(x+h) - f(x)) / h, which is essentially finding the slope of the tangent line to the curve at a specific point. The process involves substituting the root function into the limit expression, simplifying by multiplying by the conjugate to eliminate the square root in the denominator, and then taking the limit as h approaches zero. The result is simplified to 1/(2√x), and the final step is to plug in x = 7 to find the slope of the tangent line at that point, resulting in 1/(2√7). The script also briefly touches on rationalizing the denominator for a cleaner mathematical expression.
📘 Two Presentations of the Slope: Rationalized and Non-Rationalized
This paragraph presents the final result of the calculus problem in two forms: one with a rationalized denominator and one without. The rationalized form involves multiplying the expression by √7/√7 to eliminate the square root in the denominator, resulting in a slope of 7√7/14 when x = 7. The non-rationalized form retains the square root, showing the slope as 1/(2√7). The paragraph emphasizes the importance of presenting mathematical results in a clear and understandable manner, whether in simplified or rationalized form.
Mindmap
Keywords
💡Secant lines
💡Tangents
💡Instantaneous rates
💡Limits
💡Root function
💡Derivative
💡Conjugate multiply
💡Rationalize the denominator
💡Slope
💡Plug in
Highlights
Problem 10 for section 2.2 involves evaluating a limit related to secant lines, tangents, and instantaneous rates.
The function given is f(x) = √x, and the limit is to be evaluated at x = 7.
The limit to evaluate is lim(h→0) [f(x+h) - f(x)] / h.
Substituting x+h into the function results in √(x+h) - √x.
To avoid division by zero, conjugate multiplication is used.
The conjugate multiplication results in (√(x+h) + √x) / (√(x+h) - √x).
The numerator and denominator are the same, so multiplying by the conjugate does not change the expression.
After distributing and simplifying, the limit becomes 1 / (√(x+h) + √x).
The h terms cancel out, leaving 1 / (√x + √x).
Substituting x = 7 into the function gives the slope as 1 / (2√7).
Rationalizing the denominator involves multiplying by √7 / √7.
After rationalization, the slope is expressed as 7√7 / 14.
The process demonstrates the application of conjugate multiplication in evaluating limits.
The problem illustrates the concept of the derivative as a slope of the tangent line.
The solution process involves algebraic manipulation and understanding of limits.
The final answer is presented in both rationalized and unrationalized forms.
The transcript provides a step-by-step walkthrough of the problem-solving process.
The solution requires knowledge of calculus concepts such as limits and derivatives.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: