AP Calculus Practice Exam Part 10 (FR #6)
TLDRIn this educational video, the instructor engages with students in a calculus class, discussing their strengths in different mathematical areas. The focus is on implicit differentiation, with a detailed walkthrough of finding the derivative of a given equation. The class also explores finding the slope of a tangent line at specific points on a curve and identifying conditions for a vertical tangent line. The session concludes with a problem involving functions of time, calculating the rate of change of 'x' with respect to time, 'dx/dt', at a given instance. The instructor uses humor and interactive teaching to simplify complex concepts.
Takeaways
- 😀 The instructor expresses a fondness for teaching the fourth and third period classes, indicating a positive teaching experience.
- 📚 The class is focused on differentiation, specifically implicit differentiation, which is a key concept in calculus.
- 🔍 The process of implicit differentiation is explained step by step, emphasizing the importance of recognizing when to apply the derivative of y with respect to x (dy/dx).
- 📈 The instructor demonstrates how to differentiate an equation step by step, including the application of the product rule and the strategy of isolating terms with dy/dx.
- 🤔 A common mistake is pointed out where students might write the derivative incorrectly without accounting for the dy/dx in the terms.
- 📝 The strategy for solving implicit differentiation problems is to get all terms with dy/dx on one side and the rest on the other to factor it out.
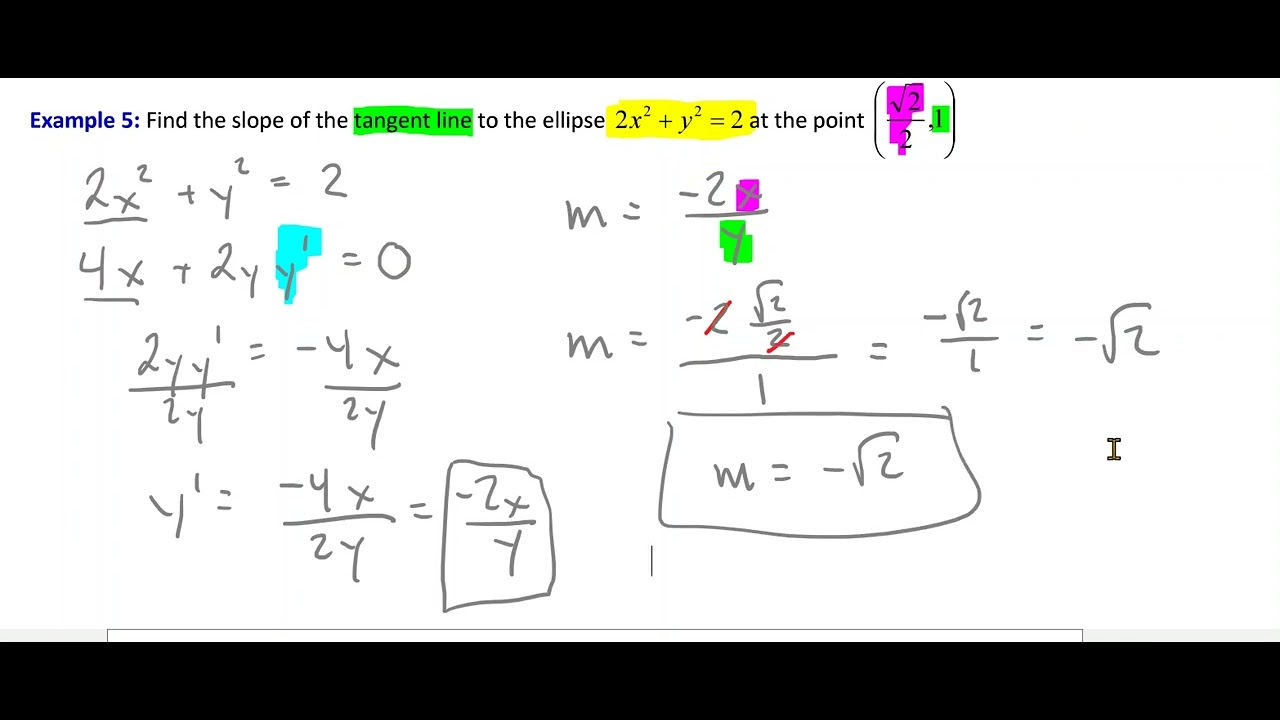
- 📉 The concept of finding the slope of a tangent line to a curve at a specific point is discussed, with the derivative being the key to finding this slope.
- 📌 The instructor shows how to find the slope of the tangent line at a point where x equals six by substituting the x and corresponding y values into the derivative.
- 🔑 The process of finding the equation of a tangent line involves taking the derivative, plugging in the x-value, and solving for the y-value if necessary.
- 🆚 The instructor compares two different methods of finding the derivative and encourages students to understand both, even if one is provided.
- 🔍 Part D introduces a new concept where x and y are functions of time, requiring a new derivative with respect to time (dx/dt or dy/dt), and demonstrates how to find dx/dt at a specific time.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is the process of implicit differentiation in calculus, specifically finding the derivative of an equation and applying it to find the slope of a tangent line at a given point.
Why does the instructor mention that the students are better at calculus and stats?
-The instructor is making a light-hearted comparison between the students' abilities in different subjects, likely to engage them and make the lesson more relatable.
What is the significance of the instructor's preference for teaching certain periods?
-The instructor's preference for teaching certain periods may indicate when they feel most energetic or when they believe the students are most receptive to learning.
What mathematical concept is introduced when discussing 'dy/dx'?
-The concept introduced when discussing 'dy/dx' is differentiation, which is the process of finding the derivative of a function with respect to a variable.
Why is the process of differentiation referred to as 'implicit' in the script?
-The process is referred to as 'implicit' because the derivative is being taken with respect to a variable that is not explicitly isolated, requiring a different approach to find the derivative.
What is the strategy the instructor teaches for solving implicit differentiation problems?
-The strategy involves getting all terms containing 'dy/dx' on one side of the equation and all other terms on the other side, then factoring out 'dy/dx' and solving for it.
How does the instructor approach finding the slope of the tangent line to a curve at a specific point?
-The instructor explains that to find the slope of the tangent line, one must first find the derivative of the function, then substitute the specific x-value (and the corresponding y-value) into the derivative.
What is the significance of finding a vertical tangent line in the context of the script?
-A vertical tangent line corresponds to a point on the curve where the slope is undefined. The instructor shows how to find such a point by setting the derivative equal to zero and solving for the variable.
How does the instructor handle the calculation of 'dx/dt' at the end of the script?
-The instructor treats 'dx/dt' as a new derivative with respect to time, rearranges the terms to isolate 'dx/dt', and then substitutes given values for x, y, and their derivatives with respect to time to find the specific value at time t equals one.
What is the final result the instructor finds for 'dx/dt' at time t equals one?
-The final result the instructor finds for 'dx/dt' at time t equals one is the value five, after substituting the given values and simplifying the expression.
Outlines
📚 Class Preferences and Implicit Differentiation
The speaker expresses their fondness for teaching particular class periods and delves into the topic of implicit differentiation. They clarify the concept by contrasting it with explicit differentiation and guide the students through the process of differentiating an equation involving both x and y variables. The explanation includes the application of the product rule and the strategy of isolating terms with 'dy/dx' to one side for clearer understanding.
🔍 Implicit Differentiation Strategy and Tangent Line Slope
Continuing the discussion on implicit differentiation, the speaker emphasizes the strategy of moving all terms with 'dy/dx' to one side and other terms to the opposite side to factor out 'dy/dx'. They then introduce the concept of finding the slope of a tangent line to a curve at a specific point by using the derivative and plugging in the x-value. The process involves solving a quadratic equation to find the corresponding y-values and calculating the slope at the point where x equals six.
📉 Vertical Tangent Line and Undefined Slope
The speaker explains how to find the x-value for which the curve has a vertical tangent line, which corresponds to an undefined slope. They demonstrate setting the derivative equal to zero to solve for y and then substituting this value back into the original curve equation to find the x-values. The process involves algebraic manipulation and solving for x, resulting in a positive x-value for the vertical tangent line.
⏱ Time-Dependent Functions and Derivatives
The script shifts to discuss functions of time, where x and y are dependent on time, and the derivative with respect to time (dx/dt and dy/dt) is required. The speaker outlines the process of finding dx/dt by taking the derivative of the given equation with respect to time and then isolating dx/dt. They provide a step-by-step guide on how to plug in the given values for x, y, and their respective time derivatives at a specific time to find dx/dt.
🎓 Final Calculation for dx/dt at Time T Equals One
The speaker concludes the lesson by calculating the value of dx/dt at time T equals one. They plug in the given values for x, y, and their derivatives with respect to time into the derived formula for dx/dt. After performing the arithmetic, they arrive at the final answer, which is presented with a touch of humor, highlighting the extensive work for a seemingly simple result.
Mindmap
Keywords
💡Implicit differentiation
💡Product rule
💡Quadratic equation
💡Slope of a tangent line
💡Derivative
💡dydx
💡Factorization
💡Greatest common factor (GCF)
💡Vertical tangent line
💡Function of time
Highlights
The instructor expresses enthusiasm for teaching the fourth and third periods, indicating a passion for the subject matter.
Introduction to implicit differentiation, emphasizing its importance in calculus and statistics.
Explanation of the differentiation process, including the derivative of 2x squared and 3y squared.
Clarification on the use of product rule when differentiating x times y.
Strategy for implicit differentiation: isolating terms with dy/dx and factoring them out.
Demonstration of simplifying the derivative expression by factoring out common terms.
Finding the slope of the tangent line to a curve at a specific point by using the derivative.
Solution of a quadratic equation to find the y-values associated with x=6.
Calculation of the slope of the tangent line at the point (6,6) and its implications.
Identification of the undefined slope as an indicator of a vertical tangent line.
Process of finding the x-value where the curve has a vertical tangent by setting the derivative to zero.
Substitution of the derived y-value into the original curve equation to solve for x.
Solution for x that results in a vertical tangent line, involving the square root of 54.
Differentiation with respect to time (dx/dt and dy/dt) for functions of time.
Finding the value of dx/dt at a specific time by plugging in given values for x, y, and their derivatives.
Final calculation resulting in the value of dx/dt at time t=1 being 5.
Emphasis on the importance of practice for understanding the process of finding tangent lines and derivatives.
Encouragement for students to complete their assigned video watching for the week.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: