Calculus AB Homework 6.2 Riemann and Trapezoidal Sums

Michelle Krummel

14 Feb 201826:43

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video tutorial guides viewers through solving unit six homework problems 15 to 19, focusing on Riemann and trapezoidal sums for approximating definite integrals. It demonstrates step-by-step calculations using various methods, including left and right Riemann sums and midpoint Riemann sums, as well as trapezoidal sums with different numbers of subintervals. The video employs a table of function values and clear examples to simplify complex integral approximations, catering to students seeking to understand numerical integration techniques.

Takeaways

📚 The video covers unit six homework problems 15 through 19, focusing on Riemann and trapezoidal sums for approximating definite integrals.
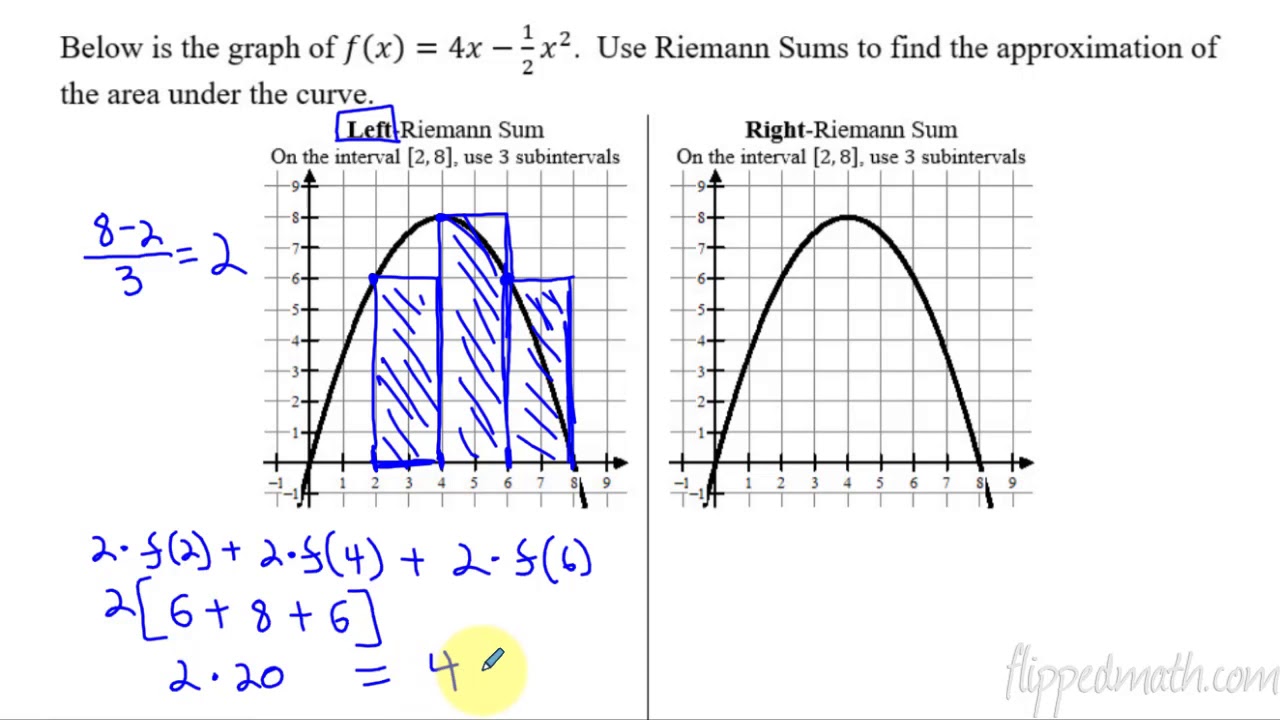
📐 Problem 15 uses a left-hand Riemann sum with two subintervals of equal length to approximate the integral from -3 to 1, resulting in an area of 14.
📉 Problem 16 employs a right-hand Riemann sum with three subintervals to estimate the integral from -3 to 9, yielding an area of 24.
📈 Problem 17 utilizes a midpoint Riemann sum with three subintervals for the integral from -3 to 9, resulting in an area of 4.
📊 Problem 18 applies a trapezoidal sum with three subintervals to approximate the integral from -3 to 3, with a final area approximation of -4.
📝 Problem 19 uses a trapezoidal sum with six subintervals for the integral from -3 to 9, resulting in an area of 8.
🧮 The video demonstrates the process of calculating areas under the curve using different summation techniques without a calculator for some parts.
📈 The script includes a detailed explanation of how to set up and calculate Riemann sums using left, right, and midpoint methods.
📉 The process of calculating trapezoidal sums is shown, emphasizing the importance of averaging the function values at the endpoints of each subinterval.
📝 The video also covers how to handle the integral of a function from 0 to π using a right-hand Riemann sum with 4 subintervals, resulting in an approximation of 5.957.
📊 An example of approximating the integral of e^(2x) from -1 to 10 using a trapezoidal sum with 4 subintervals is provided, with a final answer of 2567.927.
📘 The importance of using a table for Riemann sums is highlighted, especially for calculating function values at specific x-values within the intervals.

Q & A

What is the main topic of the video?
-The video is about working through unit six homework problems 15 through 19, which involve approximating definite integrals using Riemann and trapezoidal sums.
What is the interval for the integral in Part A of the video?
-The interval for the integral in Part A is from negative 3 to 1.
How many subintervals are used in Part A of the video?
-In Part A, two subintervals of equal length are used for the approximation.
What type of Riemann sum is used in Part A of the video?
-A left-hand Riemann sum is used in Part A of the video.
How is the height of each rectangle determined in a left-hand Riemann sum?
-In a left-hand Riemann sum, the height of each rectangle is determined by the function value at the left edge of the interval.
What is the total area of the rectangles in Part A of the video?
-The total area of the rectangles in Part A is 14.
How many subintervals are used in Part B of the video?
-In Part B, three subintervals of equal length are used for the approximation.
What type of Riemann sum is used in Part B of the video?
-A right-hand Riemann sum is used in Part B of the video.
How is the height of each rectangle determined in a right-hand Riemann sum?
-In a right-hand Riemann sum, the height of each rectangle is determined by the function value at the right edge of the interval.
What is the total area of the rectangles in Part B of the video?
-The total area of the rectangles in Part B is 24.
What is the integral being approximated in Part C of the video?
-In Part C, the integral being approximated is from negative 3 to 9.
What type of Riemann sum is used in Part C of the video?
-A midpoint Riemann sum is used in Part C of the video.
How is the height of each rectangle determined in a midpoint Riemann sum?
-In a midpoint Riemann sum, the height of each rectangle is determined by the function value at the midpoint of the interval.
What is the total area of the rectangles in Part C of the video?
-The total area of the rectangles in Part C is 4.
How many subintervals are used in Part D of the video for the trapezoidal sum?
-In Part D, three subintervals are used for the trapezoidal sum.
What is the method used to calculate the area of a trapezoid in the video?
-The area of a trapezoid is calculated by multiplying the width by the average of the two bases.
What is the total area approximation for the trapezoidal sum in Part D of the video?
-The total area approximation for the trapezoidal sum in Part D is negative 4.
What is the integral being approximated in Part II of the video?
-In Part II, the integral being approximated is from negative 3 to 9.
How many subintervals are used in Part II of the video for the trapezoidal sum?
-In Part II, six subintervals are used for the trapezoidal sum.
What is the total area approximation for the trapezoidal sum in Part II of the video?
-The total area approximation for the trapezoidal sum in Part II is 8.
What is the integral being approximated in problem 16 of the video?
-In problem 16, the integral being approximated is from 0 to PI of x sine(x) dx.
How many subintervals are used in problem 16 of the video for the Riemann sum?
-In problem 16, four subintervals of equal length are used for the Riemann sum.
What is the integral being approximated in problem 17 of the video?
-In problem 17, the integral being approximated is from negative one to 10 of e squared x squared dx.
How many subintervals are used in problem 17 of the video for the trapezoidal sum?
-In problem 17, four subintervals of equal length are used for the trapezoidal sum.
What is the integral being approximated in problem 18 of the video?
-In problem 18, the integral being approximated is from negative two to nine of P of X dx.
How many subintervals are used in problem 18 of the video for the Riemann sum?
-In problem 18, three subintervals are used for the midpoint Riemann sum.
What is the integral being approximated in problem 19 of the video?
-In problem 19, the integral being approximated is from negative two to nine of P of X dx.
How many subintervals are used in problem 19 of the video for the trapezoidal sum?
-In problem 19, six subintervals are used for the trapezoidal sum.

Outlines

00:00

📚 Riemann and Trapezoidal Sums for Integral Approximation

This paragraph introduces the topic of approximating definite integrals using Riemann and trapezoidal sums. It covers four different parts: Part A uses a left-hand Riemann sum with two subintervals to approximate an integral from -3 to 1, calculating the areas of rectangles formed by the function values at the left edge of each interval. Part B employs a right-hand Riemann sum with three subintervals for the same integral, using the right edge values and calculating the areas of the rectangles accordingly. Part C uses a midpoint Riemann sum with three subintervals, finding the average height at the midpoint of each interval. Part D applies a trapezoidal sum with three subintervals to approximate the integral from -3 to 3, calculating the areas of trapezoids formed by averaging the function values at the interval edges.

05:01

📉 Detailed Explanation of Trapezoidal Sums for Integral Approximation

This paragraph continues the discussion on approximating integrals, focusing on trapezoidal sums. It explains the process of using six subintervals to approximate an integral from -3 to 9, detailing the calculation of the areas of trapezoids by averaging the function values at the interval edges and multiplying by the interval width. The paragraph also provides a step-by-step guide on how to compute the areas of individual trapezoids and the total area approximation.

10:03

📈 Riemann Sums for Integral Approximation with Sine Function

The paragraph delves into using Riemann sums to approximate the integral of x sine x from 0 to π, with four subintervals of equal length. It describes setting up a table to find the function values (Y values) at the interval edges and using a right-hand Riemann sum to calculate the areas of rectangles formed by the right edge function values and the interval width. The process involves multiplying the function values by the interval width and summing these products to approximate the integral.

15:08

📊 Trapezoidal Sums for Integral Approximation with Exponential Function

This paragraph discusses approximating the integral from -1 to 10 of e^(2x) using a trapezoidal sum with four subintervals of equal length. It outlines the process of finding the X values by dividing the interval into four parts and calculating the corresponding Y values using the function e^(2x). The paragraph explains how to calculate the areas of trapezoids by averaging the function values at the interval edges, multiplying by the interval width, and summing these areas to get the final approximation.

20:09

🔍 Midpoint Riemann Sum and Trapezoidal Sum for Integral Approximation

The paragraph presents the approximation of the integral from -2 to 9 using both a midpoint Riemann sum with three subintervals and a trapezoidal sum with six subintervals. It explains the calculation of areas for the midpoint Riemann sum by multiplying the interval width by the function value at the midpoint. For the trapezoidal sum, it details the process of averaging the function values at the interval edges, multiplying by the interval width, and summing the areas of the resulting trapezoids.

25:12

📐 Final Calculations for Trapezoidal Sum Approximations

The final paragraph wraps up the discussion on trapezoidal sums by calculating the areas of trapezoids for the integral approximation from -2 to 9 using six subintervals. It provides a step-by-step breakdown of finding the average bases for each trapezoid, multiplying by the respective widths, and summing these areas to reach the final approximation. The paragraph emphasizes the convenience of simplifying calculations by factoring out common terms and using the properties of the trapezoidal sum method.

Mindmap

Keywords

💡Riemann Sum

A Riemann Sum is a method used in calculus to approximate the definite integral of a function. It involves breaking the area under the curve into rectangles and summing their areas. In the video, Riemann Sums are used to approximate integrals in various parts, such as the left-hand Riemann sum where the height of each rectangle is determined by the function value at the left edge of the interval.

💡Trapezoidal Sum

A Trapezoidal Sum is another technique for approximating the definite integral of a function by dividing the area under the curve into trapezoids instead of rectangles. The script describes how to calculate the area of trapezoids by averaging the two parallel sides and multiplying by the height, which is the width of the interval.

💡Definite Integral

A definite integral is a fundamental concept in calculus that represents the signed area under a curve between two points on the x-axis. The video's theme revolves around approximating these integrals using different methods like Riemann and Trapezoidal sums, as demonstrated with various function values and intervals.

💡Subintervals

Subintervals refer to the division of the interval of integration into smaller parts for the purpose of approximating the integral. In the script, the function is evaluated over these subintervals using different summation techniques, such as using two, three, or six subintervals to approximate the integral more closely.

💡Left-hand Riemann Sum

A Left-hand Riemann Sum is a specific type of Riemann Sum where the height of each rectangle is determined by the function value at the left endpoint of the subinterval. The script illustrates this concept in Part A, where the integral from -3 to 1 is approximated using two subintervals with a left-hand Riemann sum.

💡Right-hand Riemann Sum

In contrast to the left-hand Riemann Sum, a Right-hand Riemann Sum uses the function value at the right endpoint of each subinterval to determine the height of the rectangles. The script explains this method in Part B, where the integral from -3 to 9 is approximated using three subintervals with a right-hand Riemann sum.

💡Midpoint Riemann Sum

A Midpoint Riemann Sum is calculated using the function value at the midpoint of each subinterval to determine the height of the rectangles. This method is used in Part C of the script to approximate the integral from -3 to 9 using three subintervals, providing a balanced approximation between the left and right endpoints.

💡Width of Interval

The width of an interval in the context of the script refers to the length of each subinterval created when dividing the overall interval for integration. The width is crucial for calculating the area of the rectangles or trapezoids in the summation methods, as seen in the various parts of the video where the width is calculated as part of the Riemann and Trapezoidal sums.

💡Function Values

Function values are the numerical outputs of a function for specific inputs. In the script, function values are provided in a table and used to calculate the heights of the rectangles or trapezoids in the summation methods. These values are essential for approximating the integrals, as demonstrated in the video with the given function values for H(x).

💡Approximation

Approximation in the context of the video refers to the process of estimating the value of an integral using various summation techniques without performing the exact integration. The script provides step-by-step calculations for approximating integrals using Riemann and Trapezoidal sums, highlighting the process of simplification and estimation inherent in these methods.

Highlights

Introduction of the video's aim to work through unit six homework problems 15 to 19, focusing on Riemann and trapezoidal sums.

Explanation of approximating definite integrals using Riemann or trapezoidal sums with equal subintervals.

Demonstration of using a left-hand Riemann sum to approximate the integral from -3 to 1 with two subintervals.

Calculation of the area of rectangles for the left-hand Riemann sum, highlighting the process for each subinterval.

Transition to approximating the integral from -3 to 9 using a right-hand Riemann sum with three subintervals.

Description of the process to find the width of each subinterval and the height of rectangles for the right-hand Riemann sum.

Use of a calculator to simplify the calculation of the right-hand Riemann sum result.

Introduction of the midpoint Riemann sum for approximating the integral from -3 to 9 with three subintervals.

Explanation of calculating the area of rectangles using the midpoint for the height in the midpoint Riemann sum.

Transition to using a trapezoidal sum to approximate the integral from -3 to 3 with three subintervals.

Description of the process to calculate the area of trapezoids by averaging the bases and multiplying by the width.

Introduction of approximating the integral from -3 to 9 using a trapezoidal sum with six subintervals.

Calculation of the area of trapezoids for the six subintervals, emphasizing the pattern and simplification.

Transition to approximating the integral from 0 to π of x sine x dx using a right-hand Riemann sum with four subintervals.

Use of a table to organize the function values and x values for the right-hand Riemann sum calculation.

Explanation of the right-hand Riemann sum calculation using the sine function and equal subintervals.

Introduction of approximating the integral from -1 to 10 of e^(2x) dx using a trapezoidal sum with four subintervals.

Description of the process to calculate the area of trapezoids for the e^(2x) function using a calculator for efficiency.

Final calculation of the trapezoidal sum for the e^(2x) function, factoring out common terms for simplification.

Introduction of approximating the integral from -2 to 9 of P(x) dx using a midpoint Riemann sum with three subintervals.

Calculation of the area of rectangles using the midpoint Riemann sum method for the given function P(x).

Introduction of approximating the integral from -2 to 9 of P(x) dx using a trapezoidal sum with six subintervals.

Description of the process to calculate the area of trapezoids for the six subintervals of P(x) using the trapezoidal sum method.

Final calculation of the trapezoidal sum for P(x), showing the addition of areas and simplification of the result.

Transcripts

Browse More Related Video

Riemann and Trapezoidal Sums from Tables of Values

AP Calculus AB - 6.2 Approximating Areas with Riemann Sums

AP Calculus AB: Lesson 6.2 Riemann and Trapezoidal Sums

Integration and Area under a Curve

Riemann Sums

Calculus AB/BC – 6.2 Approximating Areas with Riemann Sums

Related Tags

Riemann Sums Trapezoidal Sums Integral Approximation Mathematics Education Homework Help Calculus Techniques Educational Content Video Tutorial Math Problems Integral Calculus