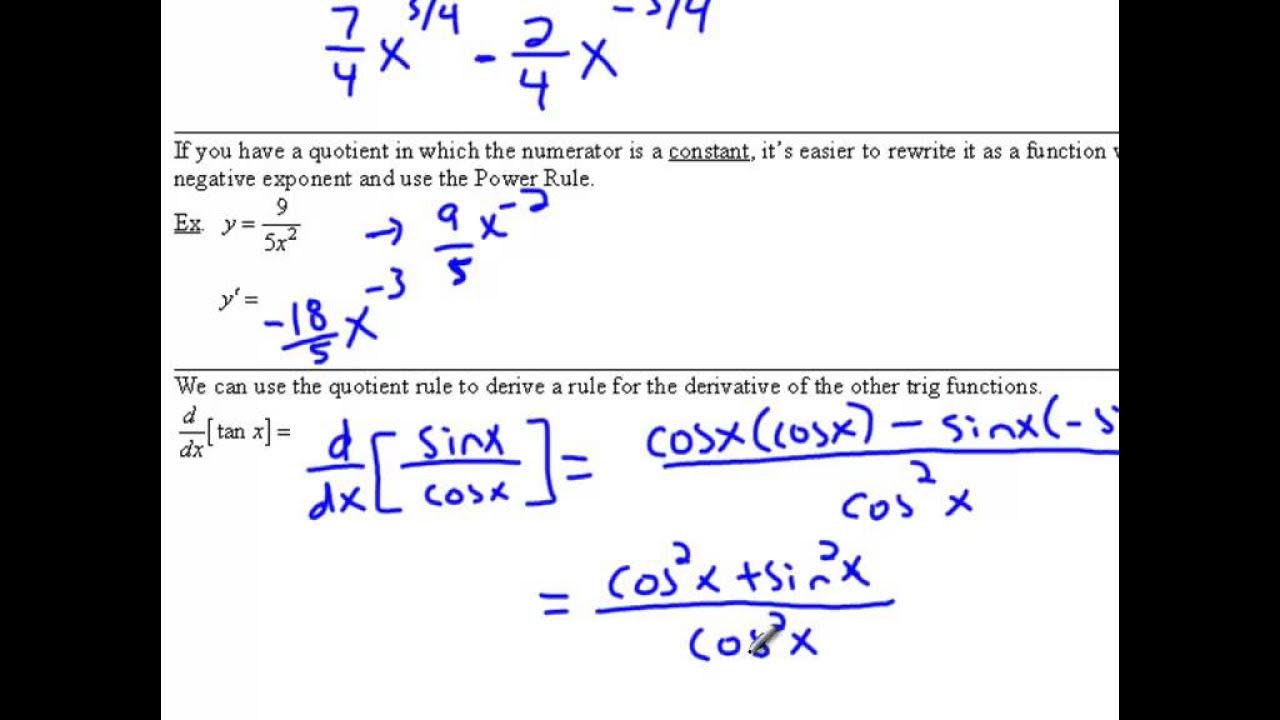AP Calculus AB: Lesson 3.3 The Quotient Rule
TLDRIn this instructional video, Michelle Crummell introduces the Quotient Rule for deriving functions in quotient form. She demonstrates the rule's application with examples, starting with basic functions and progressing to more complex scenarios, including trigonometric functions. Crummell also addresses common misconceptions about differentiating quotients and emphasizes the importance of correctly applying the Quotient Rule over simplifying the function. The lesson includes practice problems and mnemonic devices to aid memorization of derivative formulas, concluding with a look ahead to the Chain Rule in the next session.
Takeaways
- 📚 The lesson introduces the Quotient Rule for finding the derivative of functions in quotient form, emphasizing its importance for functions like u(t) and v(t).
- 🔍 The script demonstrates the process of finding derivatives for u(t) and v(t) using basic derivative rules, setting the stage for the Quotient Rule.
- 📝 An example function q(t) is created by dividing v(t) by u(t), and the quotient is simplified algebraically to prepare for derivative calculation.
- 🧐 The derivative of q(t) is calculated using sum and constant multiple rules, showing an alternative method before introducing the Quotient Rule.
- 🙅♀️ A common misconception is refuted: the derivative of a quotient (v/u) is not simply the derivative of v divided by the derivative of u.
- 🔑 The Quotient Rule formula is presented as a structured rule for differentiating quotients: \( (f/g)' = (f'g - fg')/g^2 \).
- 📈 The script compares the Quotient Rule to the Product Rule, highlighting the structural similarity and the importance of memorization.
- 📚 Several examples are worked through to apply the Quotient Rule, including derivatives of functions involving e^x, sine, and tangent.
- 📉 The script explains how to use the Quotient Rule in conjunction with other derivative rules, such as the Product Rule, for complex functions.
- 📝 The process of finding the equation of a tangent line to a function involves using the derivative to determine the slope at a specific point.
- 📉 The concept of estimating derivatives using central differences is introduced, along with its application in estimating \( g'(2.5) \) from given values.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is the quotient rule, which is used to find the derivative of functions written in the form of a quotient.
What are the functions u(t) and v(t) given to be in the transcript?
-The function u(t) is given as 2t squared, and the function v(t) is given as t cubed plus 4t.
What is the derivative of u(t) and v(t) according to the transcript?
-The derivative of u(t), denoted as u'(t), is 4t. The derivative of v(t), denoted as v'(t), is three t squared plus four.
How is the new function q(t) formed in the lesson?
-The new function q(t) is formed by taking the function v and dividing it by the function u, making it a quotient of v over u.
What is the simplified form of q(t) after algebraic manipulation?
-After algebraic manipulation, q(t) simplifies to t over 2 plus 2t to the negative 1, which is the same as 1/t squared.
What is the derivative of the function q(t) found using the sum and constant multiple rules?
-The derivative of q(t), denoted as q'(t), is one-half minus two over t squared.
What is the statement in part d of the lesson, and is it true or false?
-The statement in part d is 'the derivative of v over u is equal to the derivative of v over the derivative of u'. The statement is false, as demonstrated by the example where t equals 1.
What is the quotient rule formula?
-The quotient rule formula is given as h'(x) = (f'(x)g(x) - f(x)g'(x)) / g(x)^2, where h(x) is the quotient of f(x) over g(x).
How is the quotient rule similar to the product rule in structure?
-The quotient rule is similar to the product rule in structure in that both start with the derivative of the first function and involve the subtraction of a term involving the derivative of the second function, but the quotient rule also includes division by the square of the second function.
What are the mnemonic devices provided to remember the derivatives of the trigonometric functions secant, tangent, and cosecant?
-The mnemonic device provided is 'sexy sexy tan, minus kissy kissy cut', which helps remember the derivatives of secant (secant x tangent x), tangent (secant squared x), and cosecant (negative cosecant squared x).
How can you find the equation of the tangent line to a function at a given point using the quotient rule?
-To find the equation of the tangent line, you first find the derivative of the function using the quotient rule, then substitute the given point's x-value to find the slope (derivative value). Use the y-value of the function at that x-value and the slope to write the equation of the tangent line using the point-slope form.
What is the process of finding the equation of the normal line to a function at a given point?
-To find the equation of the normal line, you first find the derivative of the function to determine the slope of the tangent line at the given point. The slope of the normal line is the opposite reciprocal of the tangent line's slope. Then, use the y-value of the function at that x-value and the normal line's slope to write the equation of the normal line using the point-slope form.
Outlines
📚 Introduction to the Quotient Rule
Michelle Crummell introduces the Quotient Rule, a mathematical concept used to find the derivative of a function expressed as a quotient. The lesson begins with an activity to establish the need for this rule. Two functions, u(t) and v(t), are defined, and their derivatives are calculated using known derivative rules. A new function, q(t), is then created as the quotient of v(t) divided by u(t). The process of simplifying q(t) algebraically and finding its derivative using sum and constant multiple rules is demonstrated. The lesson also addresses a common misconception about taking derivatives of quotients and emphasizes the need for the Quotient Rule.
🔍 The Quotient Rule's Formula and Application
The Quotient Rule is formally introduced with its formula: if h(x) = f(x) / g(x), then h'(x) = (f'(x)g(x) - f(x)g'(x)) / g(x)². The structure of this rule is compared to the Product Rule for easier memorization. An example is provided to apply the Quotient Rule to find the derivative of a function, and the importance of not confusing the order of operations is stressed. The lesson also explains how to think about the Quotient Rule in terms of 'top' and 'bottom' rather than 'numerator' and 'denominator' for easier application.
📝 Examples of Applying the Quotient Rule
Several examples are worked through to demonstrate the application of the Quotient Rule in finding derivatives. The examples include functions with polynomials in the numerator and denominator, as well as functions involving exponential and logarithmic expressions. Each example is carefully explained, showing the step-by-step process of differentiating using the Quotient Rule. The results are simplified where possible, and the importance of correctly applying the rule is emphasized.
📉 Graph and Table Problems Using the Quotient Rule
This section of the lesson deals with graph and table problems that require the use of the Quotient Rule. The process of finding the derivative of a function at a specific point is explained, using the graph to determine the necessary values. The concept of a tangent line is introduced, and the equation for such a line is derived using the point of tangency and the slope, which is the derivative of the function at that point. The lesson also covers estimating derivatives using central differences in a table of values.
📌 Derivatives of Trigonometric Functions Using the Quotient Rule
The Quotient Rule is applied to derive the derivatives of various trigonometric functions, such as tangent, cotangent, secant, and cosecant. The process involves expressing these functions as quotients of sine and cosine functions and then differentiating them using the Quotient Rule. The resulting derivative formulas are simplified using trigonometric identities, and the importance of memorizing these derivatives for quick application is stressed.
📘 Memorization Techniques for Trigonometric Derivatives
A mnemonic device is introduced to help memorize the derivatives of the trigonometric functions. The device, 'sexy sexy tan - minus kissy kissy cut', is used to remember the derivatives of secant, tangent, cosecant, and cotangent functions. The lesson explains how to use this mnemonic in both directions to recall the derivatives quickly and accurately, emphasizing the need for memorization to save time during assessments.
📌 Tangent and Normal Line Equations Using Derivatives
The lesson concludes with problems that involve finding the equations of tangent and normal lines to a curve at a given point. The process involves using the derivative of the function at that point to determine the slope of the tangent line and the reciprocal of the slope for the normal line. Examples are provided to illustrate how to find these lines, including substituting values into the function and its derivative to find the necessary points and slopes.
Mindmap
Keywords
💡Quotient Rule
💡Derivative
💡Power Rule
💡Constant Multiple Rule
💡Sum and Difference Rule
💡Algebraic Simplification
💡Tangent Line
💡Product Rule
💡Chain Rule
💡Trigonometric Functions
Highlights
Introduction to the quotient rule for finding the derivative of functions in quotient form.
Establishing the need for a special quotient rule through an activity involving functions u(t) and v(t).
Derivation of u'(t) and v'(t) using known derivative rules.
Formation of a new function q(t) as the quotient of v(t) divided by u(t).
Algebraic simplification of q(t) to facilitate easier derivative calculation.
Derivation of q'(t) using sum and constant multiple rules combined with the power rule.
Discussion on the false statement that the derivative of v/u equals v'/u'.
Proof by counterexample that the derivative of a quotient is not simply the quotient of the derivatives.
Introduction and explanation of the quotient rule formula.
Comparison of the quotient rule to the product rule for easier memorization.
Application of the quotient rule to find the derivative of a function involving t^3 + 4t over 2t^2.
Practice examples using the quotient rule for various functions.
Use of the quotient rule to derive formulas for the derivatives of trigonometric functions like tan(x), cot(x), sec(x), and csc(x).
Mnemonic device 'sexy sexy tan - minus kissy kissy cut' to remember the derivatives of trigonometric functions.
Finding the equation of a tangent line using the quotient rule and its applications.
Derivation of the equation of a normal line to a function using the quotient rule.
Conclusion and预告 of the next lesson focusing on the chain rule.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: