Trick for Slater's Rule, calculation of screening constant and effective nuclear charge.
TLDRThis educational video explains the concept of effective nuclear charge, crucial for understanding atomic structure. It details how the presence of multiple electrons in an atom alters the perceived nuclear charge by individual electrons due to shielding effects. The formula Z - ΣJD is introduced to calculate this charge, with Z as atomic number and ΣJD as the sum of screening constants. The video provides a step-by-step guide, including examples for lithium, boron, and titanium, illustrating how to determine the effective nuclear charge for electrons in different orbitals.
Takeaways
- 🧲 The concept of effective nuclear charge is crucial for understanding the behavior of electrons in multi-electron atoms.
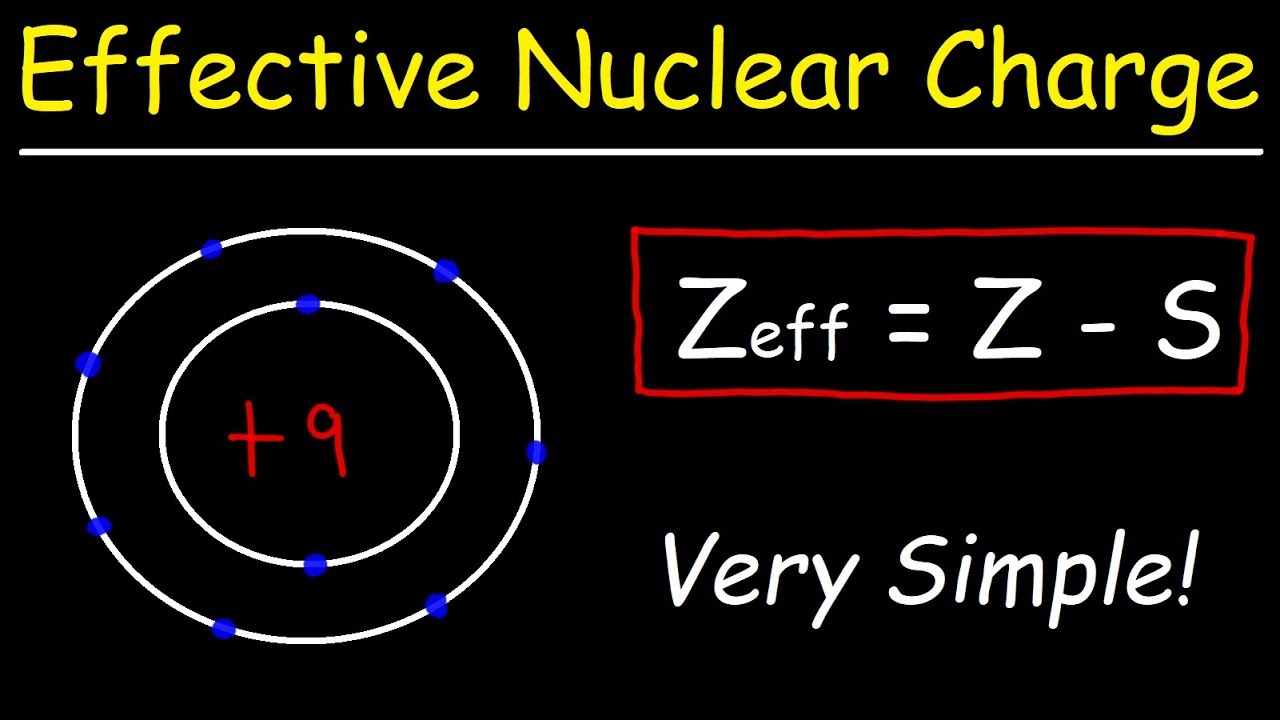
- 📊 The effective nuclear charge (Zeff) is calculated using the formula Zeff = Z - ΣJ, where Z is the atomic number and ΣJ is the sum of the screening constants.
- 🔍 Screening constants (ΣJ) represent the degree to which other electrons shield a particular electron from the nucleus.
- 🌟 The value of screening constants varies depending on the orbital and the energy level (n) of the electron.
- 📚 For s and p electrons in the same energy level (n), the screening constant is 0.35, while for n-1 it is 0.85, and for n-2, n-3, n-4, it is 1.
- 📝 When calculating for d or f electrons, the screening constant for electrons in n is 0.35, and for all others, it is 1.
- 🌐 The arrangement of electron configuration is based on the n value, grouping s and p together and d and f separately.
- 🌠 An example given in the script is lithium (atomic number 3), where the effective nuclear charge for a 4s electron is calculated to be 1.3.
- 🚀 For boron (atomic number 5), the effective nuclear charge for a 2p electron is calculated to be 2.6.
- 🌟 Titanium (atomic number 22) serves as another example, where the effective nuclear charge for a 3d electron is calculated to be 13.65.
- 👍 The video encourages viewers to like and subscribe for more educational content.
Q & A
What is the concept of effective nuclear charge?
-The effective nuclear charge is a concept that describes the net positive charge experienced by an electron in a multi-electron atom. It is less than the actual nuclear charge due to the shielding effect of other electrons present in the atom.
Why does an electron in a multi-electron atom experience less nuclear charge?
-An electron in a multi-electron atom experiences less nuclear charge because the presence of other electrons in the same or other orbitals shields it from the full charge of the nucleus.
What is the formula used to calculate the effective nuclear charge?
-The formula to calculate the effective nuclear charge is Z - ΣJ, where Z is the atomic number and ΣJ is the sum of the screening constants for all the electron shells.
What are screening constants and how are they used in the formula for effective nuclear charge?
-Screening constants are values that represent the shielding effect of electrons in different shells on the nucleus. They are used in the formula for effective nuclear charge to account for the reduction in the experienced nuclear charge due to the presence of other electrons.
What is the contribution of an electron in the n shell to the screening constant?
-The contribution of an electron in the n shell to the screening constant is 0.35 for s and p electrons, and 0.85 for electrons in the n-1 shell. For electrons in the n-2, n-3, or n-4 shells, the contribution is 1.
How is the screening constant for d or f orbitals calculated differently?
-For d or f orbitals, the screening constant is calculated by considering the contribution of 0.35 from all other electrons, and the remaining electrons contribute a value of 1, except for the last electron in the d or f orbital, which contributes 0.35.
Can you provide an example of calculating the effective nuclear charge for lithium?
-For lithium, with an atomic number of 3 and an electron configuration of 1s² 2s¹, the screening constant for the 2s electron is calculated as 1.7 (2 electrons in the 2 shell contribute 0.85 each). The effective nuclear charge is then 3 - 1.7 = 1.3.
How is the effective nuclear charge for a p electron in boron calculated?
-For boron, with an atomic number of 5 and an electron configuration of 1s² 2s² 2p¹, the screening constant for the 2p electron is calculated by adding the contributions from the 2s electrons (2 * 0.35) and the 2p electrons (2 * 0.85), resulting in 2.4. The effective nuclear charge is then 5 - 2.4 = 2.6.
What is the atomic number and electron configuration of titanium?
-Titanium has an atomic number of 22 and an electron configuration of 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d².
How is the effective nuclear charge for a d electron in titanium calculated?
-For the d electron in titanium, the screening constant is calculated by considering the contribution of 0.35 from the last d electron and 1 from all other electrons, resulting in 18.35. The effective nuclear charge is then 22 - 18.35 = 3.65.
Outlines
🔬 Understanding Effective Nuclear Charge
The first paragraph introduces the concept of effective nuclear charge, explaining how the presence of multiple electrons in an atom affects the experienced nuclear charge by an electron in an orbital. The formula for calculating effective nuclear charge, Z - ΣJD, is presented, where Z is the atomic number and ΣJD represents the sum of the screening constants for all other electrons. The paragraph details the screening constants for s and p electrons, as well as the specific values for different electron shells (n-1, n-2, etc.). An example using lithium (atomic number 3) is provided to demonstrate the calculation of effective nuclear charge, resulting in a value of 1.3.
🌟 Effective Nuclear Charge Calculations for Multiple Elements
The second paragraph continues the discussion on effective nuclear charge, providing calculations for boron and titanium. For boron (atomic number 5), the paragraph explains the process of calculating the effective nuclear charge for a p-electron, resulting in a value of 2.6. The process involves summing the contributions of electrons in different shells, considering their respective screening constants. For titanium (atomic number 22), the paragraph focuses on calculating the effective nuclear charge for a d-electron, yielding a value of 3.65. The summary includes the step-by-step breakdown of the screening constant calculation, emphasizing the contributions from electrons in s, p, and d orbitals. The paragraph concludes with an encouragement to like and subscribe for more educational content.
Mindmap
Keywords
💡Effective Nuclear Charge
💡Atomic Number
💡Electron
💡Orbital
💡Screening Constant
💡Nuclear Charge
💡Shielding Effect
💡Quantum Number
💡Electronic Configuration
💡Lithium
💡Boron
💡Titanium
Highlights
Introduction to the concept of effective nuclear charge and its importance in multi-electron atoms.
Explanation of how the presence of multiple electrons affects the experienced nuclear charge by an electron in an orbital.
The formula for calculating the effective nuclear charge: Z - ΣJD, where Z is atomic number and ΣJD is the screening constant.
Definition of screening constant and its role in determining the effective nuclear charge.
Different contributions of electrons in various orbitals: s and p electrons contribute 0.35, while electrons in n-1, n-2, n-3, n-4 contribute 0.85 and 1 respectively.
Special case for d and f orbitals where the contribution is 0.35 for d and 1 for f, with the remaining electrons contributing 1.
Presentation of a tabular column to simplify the understanding of the contributions of different orbitals.
Example calculation of effective nuclear charge for lithium (Li) using its atomic number and electronic configuration.
Step-by-step method for arranging electronic configurations based on n values for effective nuclear charge calculation.
Calculation of the screening constant for a p electron in boron (B) and its effective nuclear charge.
Grouping of s, p, and d orbitals for the calculation of effective nuclear charge in titanium (Ti).
Detailed calculation of the screening constant for a d electron in titanium, considering the contributions of all other electrons.
Final calculation of the effective nuclear charge for titanium, demonstrating the application of the formula.
Emphasis on the practical applications of understanding effective nuclear charge in atomic structure and chemistry.
Encouragement for students to like and subscribe for more educational content on the topic.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: