Lec 39 | MIT 18.01 Single Variable Calculus, Fall 2007
TLDRThe video script is a lecture on power series and their applications, delivered by a substitute professor for Professor Jerison. It covers the definition of power series, their properties, and the concept of the radius of convergence. The lecture includes examples of power series for functions like e^x, 1/(1+x), sin(x), and ln(1+x), demonstrating how to derive and manipulate these series. The professor also explains operations on power series such as multiplication, differentiation, and integration, highlighting the utility of power series in calculus. The lecture concludes with an encouragement to enroll in 18.02, a course on vector calculus, which will provide further context and understanding of the material covered.
Takeaways
- 📚 The lecture is a continuation of the topic on power series and Taylor's formula, aiming to provide further examples and applications.
- 👨🏫 Professor Jerison is absent, and a substitute professor is leading the class, emphasizing the importance of reviewing power series concepts.
- 🔍 Power series are introduced as a way to express functions as sums of integral powers of x, with coefficients that can be any number.
- 📈 Power series can be thought of as generalized polynomials, with a key difference being the existence of a radius of convergence, R, which determines the domain of convergence.
- 📘 The professor highlights that within the radius of convergence, a function behaves like a polynomial, allowing for differentiation and the application of Taylor's formula.
- 📝 An example of a power series is given for the exponential function e^x, where all derivatives at x=0 are 1, leading to a series of terms with factorials in the denominator.
- 🤔 The professor addresses a common question regarding how far one must write out a power series, emphasizing the importance of showing the pattern for clarity.
- 📊 The lecture includes a discussion on the radius of convergence, explaining that it can be found by examining the behavior of the series at the edges of its domain.
- 📚 The professor provides a power series expansion for the function 1/(1+x), demonstrating the use of the geometric series and its properties.
- 📐 The lecture explores the power series for trigonometric functions, specifically sin(x), and how to derive it using Taylor's formula and the properties of derivatives.
- 🧩 The professor concludes with a discussion on operations that can be performed on power series, such as multiplication, differentiation, and integration, to derive new series.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is power series, including their properties, applications, and examples of their use in various mathematical functions.
What is a power series and how is it related to polynomials?
-A power series is a way of expressing a function as a sum of integral powers of a variable, x. It behaves almost exactly like polynomials, with the main difference being the introduction of a radius of convergence, R.
What is the radius of convergence and why is it important?
-The radius of convergence, R, is a number between 0 and infinity (inclusive) that determines the interval in which the power series converges to a finite value. It is important because it dictates the domain for which the power series representation of a function is valid.
What is the significance of Taylor's formula in the context of power series?
-Taylor's formula is significant because it allows you to express the coefficients of a power series in terms of the derivatives of the function at a specific point, usually x = 0.
Can you provide an example of a power series from the lecture?
-One example given in the lecture is the power series for the exponential function e^x, which is 1 + x + x^2/2! + x^3/3! + ... and so on.
How does the lecture address the question of which functions can be written as power series?
-The lecture states that any function that has a reasonable expression can be written as a power series, including common functions from calculus like sines, cosines, and tangents.
What is the geometric series and how does it relate to the power series for 1/(1+x)?
-The geometric series is a power series with a constant ratio between consecutive terms. The function 1/(1+x) can be expressed as a geometric series with alternating signs, which is derived from the general formula for a geometric series.
How is the power series for sin(x) derived using Taylor's formula?
-The power series for sin(x) is derived by computing the derivatives of sin(x) and evaluating them at x = 0, then applying Taylor's formula to express sin(x) as a sum of terms involving these derivatives and their respective factorials in the denominator.
What is the radius of convergence for the power series of sin(x) and why is it infinity?
-The radius of convergence for the power series of sin(x) is infinity because the general term of the series, which involves x raised to an odd power divided by the corresponding factorial, converges to 0 for any value of x, indicating that the series converges for all x.
Can you explain how the lecture derives the power series for ln(1+x)?
-The lecture derives the power series for ln(1+x) by integrating the power series of 1/(1+t) term by term with respect to t from 0 to x, and then evaluating the result at t = x and t = 0 to obtain the power series for ln(1+x).
What is the error function and how does the lecture discuss its power series expansion?
-The error function, often used in probability theory, is defined as the integral of e^(-t^2) from 0 to x. The lecture discusses its power series expansion by substituting -t^2 into the power series for e^x and integrating term by term.
Outlines
📚 Introduction to Power Series and Course Logistics
The professor begins by acknowledging the support for MIT OpenCourseWare, which enables the free distribution of educational resources. He substitutes for Professor Jerison, who is in London, Ontario, and outlines the agenda for the day, which includes a review of power series and Taylor's formula, examples and applications, and a course evaluation survey. The professor also mentions a handout for the end-of-term and advises students to check the website for office hours and final exam details. He emphasizes the importance of understanding power series as generalized polynomials and introduces the concept of the radius of convergence, R, as a key factor in determining the series' behavior.
🔍 Radius of Convergence and Taylor's Formula
The professor explains the concept of the radius of convergence, stating that within this radius, a function behaves like a polynomial, having all its derivatives. He discusses Taylor's formula, which expresses the coefficients of a power series in terms of the function's derivatives at a point, typically zero. The professor then provides an example of the exponential function e^x, demonstrating how its power series is derived from its derivatives, all of which are e^x, evaluated at x = 0. He also addresses a question about the extent to which a power series must be written out to be considered complete, emphasizing the importance of recognizing the pattern.
📈 Power Series Expansions for Common Functions
The professor delves into the power series expansions for several common functions, such as sines, cosines, and tangents, which are all available in calculus. He provides a detailed example of the geometric series and its relation to the function 1/(1+x), highlighting the importance of the radius of convergence, which in this case is 1. The professor also discusses the implications of the graph of the function at x = -1, where the series does not converge, indicating the limit of the radius of convergence.
📘 Derivatives and the Power Series of Sine and Cosine
The professor continues with the topic of derivatives, showing how the power series for sine and cosine can be derived using Taylor's formula. He explains the periodic nature of the derivatives of sine and cosine and how they result in a repeating pattern of coefficients in their power series expansions. The professor emphasizes that the radius of convergence for the sine function's power series is infinity, meaning it converges for all values of x. He also explains the mathematical reasoning behind the convergence of the series terms to zero as n approaches infinity.
🤔 Exploring the Properties and Operations on Power Series
The professor discusses the properties of power series and the operations that can be performed on them, such as multiplication and differentiation. He provides an example of multiplying the power series of sine by x to obtain a new series, whose radius of convergence is the minimum of the two original series. The professor also explains how differentiation can be used to find the power series for cos(x) from that of sin(x), maintaining the same radius of convergence.
🧮 Integration and the Power Series for ln(1+x)
The professor explores the application of power series to integration, specifically finding the power series for ln(1+x) by integrating the known power series of 1/(1+t). He demonstrates the process of integrating term by term and evaluating the result at x and 0 to arrive at the power series expansion for ln(1+x). The professor notes that the radius of convergence for this series is 1, reflecting the behavior of the original function outside this range.
🌐 Substitution in Power Series and the Error Function
The professor concludes the lesson by discussing substitution in power series as a method to find new expansions. He uses the example of e^(-t^2) and shows how substituting x = -t^2 into the power series expansion for e^x yields a new series. The professor also introduces the error function, which is derived from the integral of e^(-t^2) and normalized by a factor of 2 over the square root of pi. He outlines the process of finding the power series expansion for the error function, emphasizing its importance in probability theory.
📘 Course Conclusion and Encouragement for Further Studies
In the final paragraph, the professor wraps up the lesson and encourages students to take the next course, 18.02, which covers vector calculus. He suggests that this course will provide context for the material covered in the current course and explain certain concepts in more depth. The professor also mentions a poem by Professor Jerison that illustrates the unification of various calculus rules under the chain rule, emphasizing the interconnectedness of mathematical concepts.
Mindmap
Keywords
💡Power Series
💡Radius of Convergence
💡Taylor's Formula
💡Differentiation
💡Integration
💡Exponential Function
💡Trigonometric Functions
💡Geometric Series
💡Error Function
💡Operations on Power Series
Highlights
Power series are a way of writing a function as a sum of integral powers of x, behaving similarly to polynomials.
A power series can have a finite number of terms, with all higher coefficients equal to zero, making it a special case.
The radius of convergence, R, determines the interval of x values for which the power series converges.
Inside the radius of convergence, a function has all its derivatives, similar to polynomials.
Taylor's formula expresses the coefficients of a power series in terms of the function's derivatives at x=0.
The exponential function e^x has a power series with all coefficients equal to 1, discovered by Leonhard Euler.
The radius of convergence for the power series of e^x is infinity, meaning it converges for any value of x.
Any function with a reasonable expression, such as trigonometric functions, can be written as a power series.
The power series for 1/(1+x) is derived from the geometric series and has a radius of convergence of 1.
The sine function's power series expansion is computed using Taylor's formula, resulting in a series with alternating signs and increasing factorials in the denominator.
The radius of convergence for the sine function's power series is infinity, as the general term converges to 0 for any fixed x.
Power series can be manipulated through operations such as multiplication, differentiation, and integration.
The product of two odd functions, like x and sin(x), results in an even function, reflected in the even powers of x in their power series.
Differentiating a power series term by term allows finding the power series for the derivative of the function, like cos(x) from sin(x).
Integration of a power series term by term is demonstrated with the natural log function ln(1+x).
The power series for e^(-t^2) is obtained by substituting x with -t^2 in the power series expansion for e^x.
The error function, important in probability theory, is defined and its power series expansion is derived.
The course 18.02 on vector calculus is recommended as a follow-up to deepen understanding and provide context for the concepts learned.
Transcripts
Browse More Related Video
Lec 38 | MIT 18.01 Single Variable Calculus, Fall 2007
Calculus Chapter 1 Lecture 4 Computing Taylor Series

Calculus Chapter 1 Lecture 5 Convergence
Calculus Chapter 5 Lecture 54 Power Series
Ratio Test -- Radius of Convergence | MIT 18.01SC Single Variable Calculus, Fall 2010
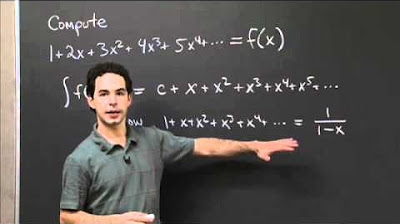
Integration of Taylor's Series | MIT 18.01SC Single Variable Calculus, Fall 2010
5.0 / 5 (0 votes)
Thanks for rating: