Lec 13 | MIT 18.01 Single Variable Calculus, Fall 2007
TLDRThis educational video script from an MIT OpenCourseWare lecture focuses on the concept of related rates, a fundamental topic in calculus. The professor illustrates the application of related rates using two examples: one involving a right triangle and the other a conical tank being filled with water. The script also introduces Newton's method, a powerful numerical technique for finding roots of equations, demonstrated through the example of solving for the square root of 5. The professor guides students through the process, emphasizing the importance of understanding the underlying principles and the practical applications of these mathematical concepts.
Takeaways
- 📚 The lecture is a continuation of a previous session on related rates, focusing on the application of differentiation to solve problems involving changing quantities.
- 🚔 The first example involves a scenario with a right triangle, a road, and a police monitoring situation, where the goal is to determine if a vehicle is speeding based on the rate of change of distance.
- 📐 The professor emphasizes the importance of implicit differentiation in solving related rates problems, as it allows for direct differentiation of equations without the need to solve for one variable in terms of another.
- 🔢 The concept of similar triangles is used to establish a relationship between the changing dimensions in the conical tank example, which is crucial for setting up the volume and rate of change equations.
- 💧 The second example problem involves a conical tank being filled with water, where the challenge is to find the rate at which the water level is rising at a certain depth.
- 📉 The lecture also covers the application of calculus to optimization problems, such as finding the lowest point of a curve representing a physical system like a suspended ring or a suspension bridge.
- 🔍 The professor demonstrates the use of implicit differentiation to find the point of equilibrium on a curve, which is where the tangent line is horizontal, indicating the minimum or maximum.
- 🎯 Newton's method is introduced as a powerful application of calculus for finding numerical solutions to equations, with the specific example of finding the square root of 5.
- 📈 The script illustrates the iterative process of Newton's method, showing how an initial guess can be refined through calculation to approximate a root of an equation with increasing accuracy.
- 🤔 The professor encourages students to ask questions and engage with the material, highlighting the importance of understanding the underlying concepts and methods in calculus.
Q & A
What is the purpose of MIT OpenCourseWare and how can one support it?
-MIT OpenCourseWare aims to offer high-quality educational resources for free. Support can be provided through donations or by viewing additional materials from hundreds of MIT courses available at ocw.mit.edu.
What is the main topic of the lecture in the provided transcript?
-The main topic of the lecture is related rates, with a focus on using differentiation to solve problems involving changing quantities over time.
What is the significance of the number 95 feet per second in the context of the lecture?
-The number 95 feet per second is mentioned as an approximate speed limit, which is being compared to the rate at which a car is approaching a police officer in the example problem.
How is the right triangle used in the first example problem involving a car and a police officer?
-The right triangle is used to establish a relationship between the distances: the distance the car is moving away from the road (x), the distance from the car to the police officer (D), and the perpendicular distance from the car to the road (30 feet). The relationship is given by the equation x^2 + 30^2 = D^2.
What is the rate at which the distance D is changing in the first example, and what does it imply?
-The rate at which the distance D is changing (dD/dt) is -80 feet per second, indicating that the distance D is decreasing at a rate of 80 feet per second as the car moves towards the police officer.
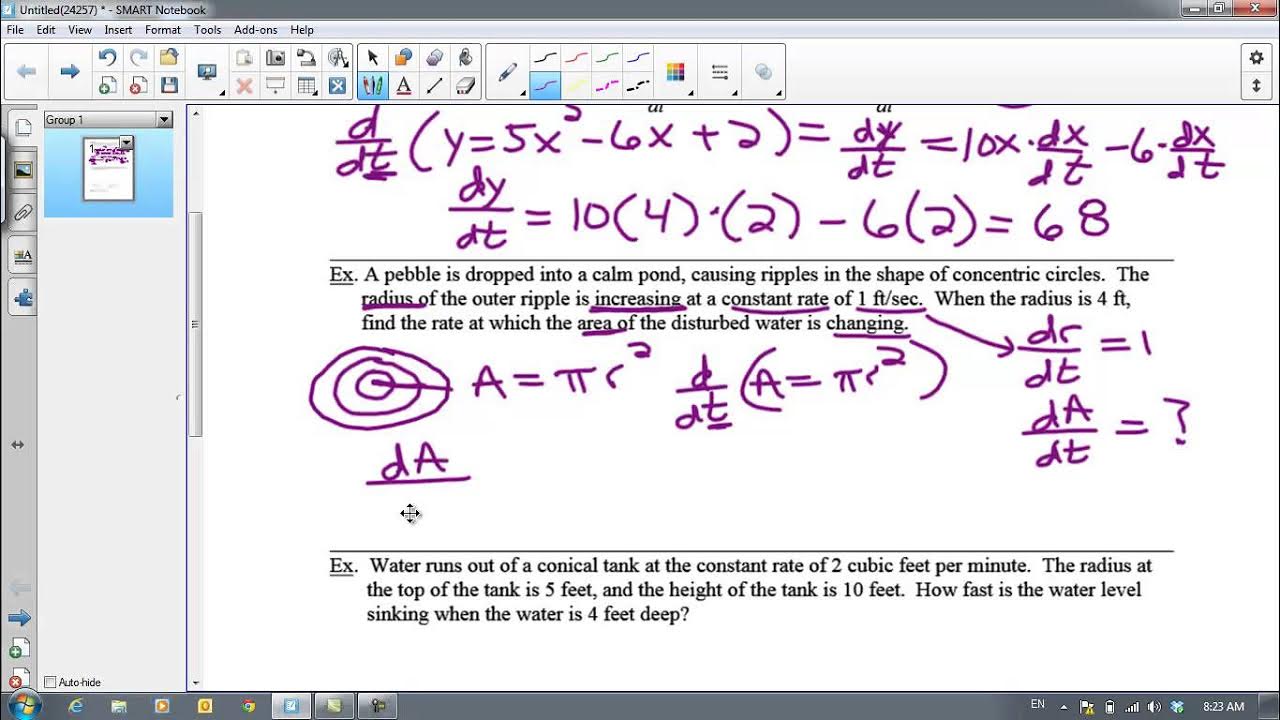
What is the second example problem about and what is the question being asked?
-The second example problem involves a conical tank being filled with water at a rate of 2 cubic feet per minute. The question is to determine how fast the water level is rising when the water depth is 5 feet.
What is the significance of the similar triangles in the conical tank problem?
-The similar triangles are used to establish a relationship between the radius of the water surface (r) and the height of the water (h) in the tank, which is given by the ratio r/h = 4/10 or simplified to 2/5.
What is the volume formula used for the conical tank and how is it applied?
-The volume formula used for the conical tank is V = (1/3) * π * r^2 * h, where r is the radius of the water surface and h is the height of the water. This formula is applied to find the rate at which the water level is rising (dh/dt).
What is the method used to find the rate of change of the water level (dh/dt) in the conical tank example?
-The method used is implicit differentiation. The volume formula is differentiated with respect to time, and then the relationship between r and h is substituted to solve for dh/dt.
What is the final calculated rate at which the water level is rising when the depth is 5 feet in the conical tank example?
-The final calculated rate at which the water level is rising when the depth is 5 feet is dh/dt = 1/(2π) feet per second.
What is the concept of related rates and how does it apply to the problems discussed in the lecture?
-The concept of related rates involves keeping track of how one variable changes in relation to another. In the context of the lecture, it applies to problems where one variable (like volume or height) is changing over time, and the relationship between variables is established using the chain rule in differentiation.
Outlines
📚 Introduction to Related Rates and Donations to MIT OpenCourseWare
The script begins with a reminder that the content is provided under a Creative Commons license and encourages donations to MIT OpenCourseWare to support free educational resources. The professor then introduces the topic of related rates, referencing a previous problem involving geometry and a right triangle. The scenario involves a road, a police monitoring station, and a vehicle moving in one direction. The distances between the vehicle, the road, and the police station are given as part of a right triangle with sides 3, 4, and 5, and the rate of change of the distance to the police is discussed in the context of speeding.
🔍 Implicit Differentiation and Solving for Speed
The professor continues the lecture by discussing implicit differentiation as a method to solve related rates problems. Using the given scenario, the professor sets up the problem with the relationship x^2 + 30^2 = D^2 and the rate of change dD/dt = -80 feet per second. The process involves differentiating the equation with respect to time, without substituting constants prematurely, and solving for dx/dt to determine if the vehicle is speeding. The conclusion is that the vehicle is indeed speeding, as the rate of approach towards the police is faster than the speed limit.
💧 Filling a Conical Tank: Related Rates and Volume
The script moves on to a second example involving a conical tank being filled with water. The tank has a radius of 4 feet and a depth of 10 feet, and water is being added at a rate of 2 cubic feet per minute. The goal is to determine how fast the water level is rising when it reaches a depth of 5 feet. The professor explains the importance of setting up diagrams and variables, using similar triangles to establish a relationship between the radius of the water's surface (r) and its height (h), and then setting up equations for the volume of the water and its rate of change.
📈 Differentiation and Calculation of Water Level Rise
The professor demonstrates how to use implicit differentiation to solve for the rate at which the water level is rising (dh/dt). Starting with the volume of a cone formula, V = (1/3) * π * r^2 * h, and substituting r as a function of h, the professor shows the process of differentiating the volume with respect to time to find dv/dt. The chain rule is applied to solve for dh/dt when h equals 5 feet, concluding with the formula dh/dt = 1/(2 * π) feet per second.
🔌 Application of Related Rates to a Physical Problem
The script presents a physical application of related rates by discussing a scenario with a ring and a flexible string. The professor explores where the ring will settle if the ends of the string are at different heights. Through a demonstration with volunteers, the professor shows that the ring settles at a point that can be determined mathematically, relating it to the concept of potential energy and the lowest energy state.
🌉 Suspension Bridge Problem and Minimization
The professor introduces a problem related to the construction of a suspension bridge, using a string and a ring to illustrate the concept. The goal is to find where the ring settles when the string is fixed at two points with different heights. The problem is set up by labeling points on the diagram and identifying the constraint that the total length of the string is constant. The professor explains that the problem involves minimizing the y-coordinate of the ring's position, subject to this constraint.
📐 Analyzing the Constraint Curve and Differentiation
The script delves into the analytical aspect of the suspension bridge problem by describing the constraint curve as an ellipse. The professor uses the Pythagorean theorem to express the lengths of the string segments and sets up an equation where the sum of the square roots of these lengths is constant. Implicit differentiation is used to find the relationship between x and y, leading to an equilibrium condition that reveals the symmetry in the problem.
🔄 Interpreting the Equilibrium Condition and Symmetry
The professor interprets the equilibrium condition derived from the previous step, explaining that it represents the angles alpha and beta being equal, indicating a hidden symmetry in the problem. This symmetry implies that the tension on the two lines of the string is the same, leading to a balanced distribution of load, which is a principle used in the construction of suspension bridges.
🎯 Newton's Method for Solving Equations
The script concludes with an introduction to Newton's method, a numerical technique for solving equations. The professor illustrates the method using the example of finding the square root of 5, by setting up a function f(x) = x^2 - 5 and aiming to solve f(x) = 0. The method involves making an initial guess, using the tangent line at that point as an approximation, and iteratively refining the guess. The professor outlines the formula for Newton's method and demonstrates its effectiveness through several iterations, showing rapid convergence to the accurate value.
🔢 Iterative Refinement in Newton's Method
The professor continues the discussion on Newton's method by providing the formula for the nth term and applying it iteratively to improve the guess for the square root of 5. The script shows the calculations for the first few iterations and notes the rapid improvement in accuracy, highlighting the power and efficiency of Newton's method for finding numerical solutions to equations.
Mindmap
Keywords
💡Related Rates
💡Differentiation
💡Implicit Differentiation
💡Right Triangle
💡Conical Tank
💡Volume of a Cone
💡Chain Rule
💡Max-Min Problem
💡Ellipse
💡Newton's Method
💡Tangent Line
Highlights
Introduction to related rates in calculus with an example involving geometry and a right triangle.
Setting up a real-world problem involving a police monitoring situation with a right triangle and calculating speed.
Differentiation of the relationship between the lengths of sides in a right triangle using implicit differentiation.
Solving for the rate of change of distance with respect to time in a given scenario.
Demonstration of how to determine if a vehicle is speeding by comparing the rate of change of distance to the speed limit.
Introduction of a conical tank problem to find the rate at which water is rising.
Use of similar triangles to establish a relationship between the radius and height of the water in the conical tank.
Derivation of the formula for the volume of water in the conical tank and its relation to the rate of change of volume.
Application of implicit differentiation to find the rate at which the water level is rising in the tank.
Calculation of the rate of water level rise in the conical tank when the water depth is 5 feet.
Discussion on the importance of understanding the relationship between different variables in related rates problems.
Introduction to a max-min problem involving a ring and parachute string to find the equilibrium point.
Geometric interpretation of the problem using an ellipse and the concept of minimizing potential energy.
Use of implicit differentiation to find the critical points for the max-min problem.
Explanation of the symmetry in the problem and its relation to the angles and tensions in the string.
Introduction to Newton's method as a numerical approach to solving equations.
Illustration of Newton's method using the example of finding the square root of 5.
Derivation of the formula for Newton's method and its application to iteratively improve the guess for the root.
Demonstration of the rapid convergence of Newton's method to the accurate value of the square root of 5.
Discussion on the practical applications of Newton's method in calculators and numerical problem-solving.
Transcripts
Browse More Related Video

Step by Step Method of Solving Related Rates Problems - Conical Example
Related Rates Day 1

Calculus 3: The Chain Rule (Video #15) | Math with Professor V

Lec 14: Non-independent variables | MIT 18.02 Multivariable Calculus, Fall 2007

Ultimate Related Rates Study Guide (cars approaching an intersection, water into a tank, $ more)

Related Rates
5.0 / 5 (0 votes)
Thanks for rating: