Discrete vs. Continuous Relationships Tutorial
TLDRIn the 'Friendly Math 101' video, the instructor clearly distinguishes between discrete and continuous relationships. Discrete items are countable and indivisible, such as people or tickets, while continuous variables can be broken down into fractions or decimals, like height or temperature. The video uses graphs to illustrate the difference, with continuous graphs showing connected points and discrete graphs showing disconnected points. Everyday examples solidify the concepts, emphasizing that discrete relationships involve counting (e.g., students, text messages) and continuous relationships involve measuring (e.g., time, weight). The lesson concludes by identifying whether various scenarios are discrete or continuous, reinforcing the fundamental mathematical concepts.
Takeaways
- 📚 Discrete things cannot be broken down into fractions or decimals and are typically countable.
- 📏 Continuous things can be broken down into fractions and decimals and are usually measured.
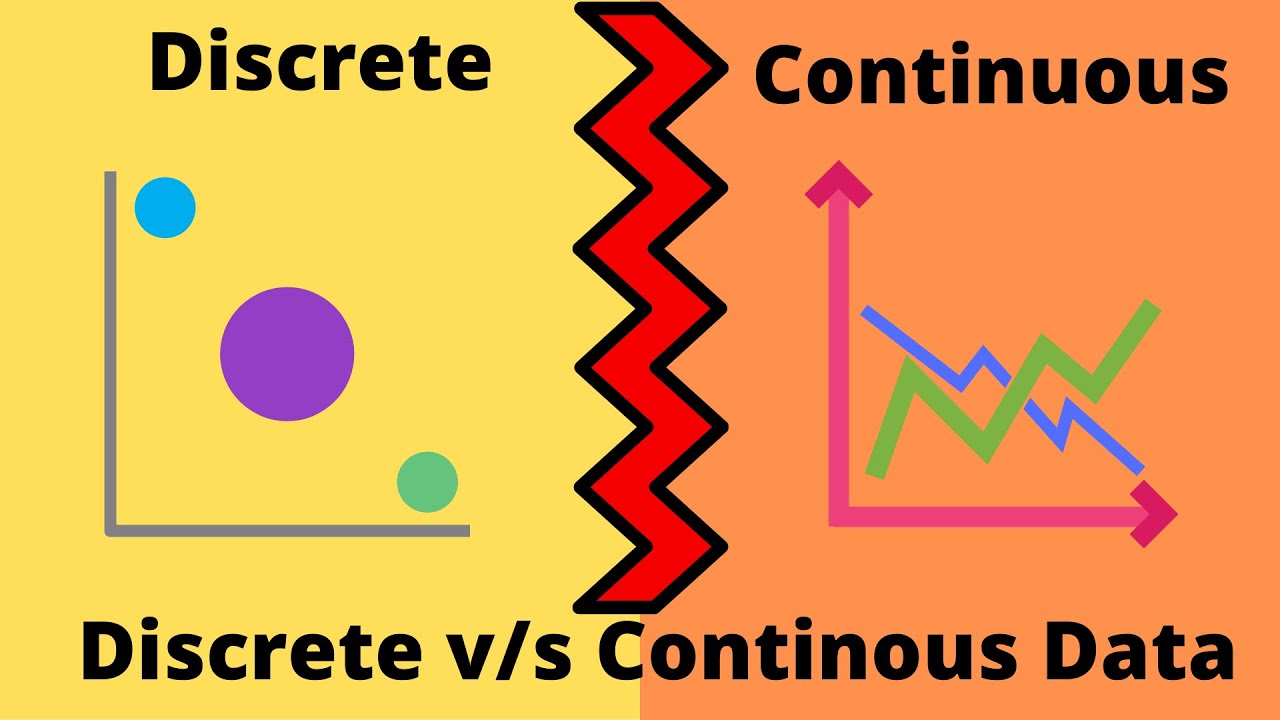
- 📈 In graphs, continuous relationships are represented by connected points, while discrete relationships show disconnected points.
- 🎟️ An example of a discrete relationship is purchasing tickets, as you cannot buy half a ticket.
- 🏫 The number of students in a classroom is discrete because students cannot be divided into fractions.
- 📱 Text messages are discrete as you cannot receive half a message.
- 📚 Books in a library are discrete entities, as they cannot be broken down into parts.
- ⏰ Time is an example of a continuous relationship, as it can be measured in fractions like half a second.
- 🌡️ Temperature is continuous and can be expressed in decimals, such as seventy-five point two degrees.
- 🏋️♂️ Weight, distance, and height are continuous measurements.
- 🛍️ Buying clothes is a discrete relationship because clothes are counted, not measured.
- 👩⚕️ The number of doctors is discrete, as people (and thus doctors) are counted, not measured.
- ⏱️ The time it takes to run a mile is continuous because time is measured and can be fractional.
- 🦒 Counting animals out of a zoo is a discrete relationship, as animals are whole entities that are counted.
- 💇♀️ The length of hair growth per day is continuous as hair can grow in fractions of an inch.
Q & A
What is the main difference between discrete and continuous relationships?
-Discrete relationships involve things that cannot be broken down into fractions or decimals and are typically countable, whereas continuous relationships involve things that can be broken down into fractions and decimals and are typically measured.
How can you determine if a graph represents a discrete or continuous relationship?
-If all the points on the graph are connected between the start and the end, it represents a continuous relationship. If the points are not connected, it represents a discrete relationship.
What is an example of a discrete situation mentioned in the script?
-Purchasing tickets is an example of a discrete situation because you cannot purchase half a ticket; it's a whole or nothing scenario.
How does the number of students in a classroom relate to discrete or continuous?
-The number of students in a classroom is an example of a discrete relationship because students are counted and cannot be broken down into fractions.
What is an example of a continuous situation mentioned in the script?
-Temperature is an example of a continuous situation because it can be measured in decimals and fractions, such as seventy-five point two degrees.
How can text messages be categorized in terms of discrete or continuous?
-Text messages are discrete because you receive them in whole units and cannot receive half a message.
What is the difference between counting and measuring in the context of discrete and continuous?
-Discrete things are counted, such as tickets, students, text messages, and books. Continuous things are measured, such as time, temperature, weight, distance, and height.
According to the script, why is the relationship of buying clothes considered discrete?
-Buying clothes is considered a discrete relationship because clothes are counted and not measured; you buy whole clothes, not fractions of them.
How does the number of doctors relate to the concept of discrete relationships?
-The number of doctors is discrete because doctors are counted individuals, and you cannot have half a doctor in the same way you cannot have half a person.
Why is the time it takes to run one mile considered a continuous relationship?
-The time it takes to run one mile is considered a continuous relationship because time can be measured in fractions of a second, such as half a second.
What makes the length hair grows per day an example of a continuous relationship?
-The length hair grows per day is an example of a continuous relationship because hair growth can be measured in fractions of an inch, such as half an inch.
Outlines
📚 Discrete vs. Continuous Relationships
This paragraph introduces the concepts of discrete and continuous relationships in mathematics. Discrete items are countable and cannot be divided into fractions or decimals, such as people or tickets. Continuous items, on the other hand, can be measured and broken down into fractions or decimals, like height or temperature. The paragraph explains how to differentiate between discrete and continuous by looking at graphs, where continuous graphs have all points connected and discrete graphs have disconnected points. Examples provided include purchasing tickets, counting students, and receiving text messages as discrete, while measuring time, temperature, and weight are continuous.
🔍 Applying Discrete and Continuous Concepts
The second paragraph delves into applying the concepts of discrete and continuous relationships to real-world scenarios. It discusses how to identify whether a situation involves counting (discrete) or measuring (continuous). Examples given include counting zoo animals, which is discrete, and measuring hair growth per day, which is continuous. The paragraph also touches on other scenarios such as buying clothes and counting doctors, both of which are discrete, and measuring the time it takes to run a mile, which is continuous. The summary concludes with an invitation to subscribe to the channel for more math tutorials.
Mindmap
Keywords
💡Discrete
💡Continuous
💡Graphs
💡Counted
💡Measured
💡Relationships
💡Tickets
💡Students
💡Text Messages
💡Books
💡Time
Highlights
Discrete things cannot be broken down into fractions or decimals and are typically countable.
Continuous situations can be broken down into fractions and decimals and are measured.
A graph is continuous if all points are connected between the start and end.
A graph is discrete if the points are not connected.
Example 1: Purchasing tickets is a discrete relationship as you cannot purchase half a ticket.
Example 2: The number of students in a classroom is discrete as students cannot be broken down into fractions.
Example 3: Text messages are discrete as you receive the entire message, not a fraction of it.
Example 4: Books in a library are discrete as they cannot be broken down into fractions or decimals.
Continuous examples include time, which can be measured in fractions like half a second.
Temperature is a continuous variable as it can be expressed in decimals like seventy-five point two degrees.
Weight, distance, and height are also continuous as they are measured.
Discrete things are counted, such as tickets, students, text messages, and books.
Continuous things are measured, including time, temperature, weight, distance, and height.
Buying clothes is a discrete relationship because clothes are counted, not measured.
The number of doctors is discrete as doctors are counted and cannot be divided into fractions.
The time it takes to run one mile is continuous as time is measured and can be in fractions.
Counting animals out of a zoo is discrete because animals are whole and cannot be divided.
The length hair grows per day is continuous as it can be measured in fractions like half an inch.
Transcripts
Browse More Related Video

Continuous vs Discrete Data

Discrete and continuous random variables | Probability and Statistics | Khan Academy

Types of Data: Categorical vs Numerical Data
Discrete v/s Continuous Data - What ? How ? || Discrete Data || Continuous Data || Basic Statistics

Probability Distribution Functions (PMF, PDF, CDF)

Introduction to Discrete Random Variables and Discrete Probability Distributions
5.0 / 5 (0 votes)
Thanks for rating: