Types of Data: Categorical vs Numerical Data

365 Data Science
9 Oct 201904:13
EducationalLearning
32 Likes 10 Comments

TLDRThis script introduces two primary types of data: categorical and numerical. Categorical data encompasses groups or categories such as car brands and yes/no answers. Numerical data is further divided into discrete and continuous subsets. Discrete data includes countable integers like the number of children desired or SAT scores. Continuous data, on the other hand, represents infinite values such as weight, height, area, distance, and time. The script illustrates the concepts with examples and highlights the distinction between discrete and continuous data, emphasizing the infinite possibilities of continuous variables despite technological constraints in measurement.

Takeaways
  • 📊 Data can be categorized into two main types: categorical and numerical.
  • 🏷️ Categorical data describes categories or groups, such as car brands or yes/no answers.
  • 🔢 Numerical data represents numbers and is further divided into discrete and continuous subsets.
  • 📏 Discrete data is countable and finite, like the number of children one wants to have or SAT exam scores.
  • 📐 Continuous data is infinite and can take on any value within a range, such as weight or height.
  • 🔍 Understanding the range and granularity of data points is crucial for defining discrete data, like SAT scores ranging from 600 to 2400 in increments of 10.
  • 🤔 The concept of discrete data is easier to grasp by contrasting it with continuous data.
  • 📚 Examples of discrete data include university grades, the number of objects, and physical money.
  • 📏 Money is discrete because it is typically measured in whole units like cents or dollars.
  • 🌡 Continuous data examples include weight, height, area, distance, and time, which can vary by infinitely small amounts.
  • ⏳ Time on a clock may appear discrete due to technological limitations, but time itself is continuous and can be measured to infinite precision.
Q & A

  • What are the two main types of data mentioned in the script?

    -The two main types of data mentioned are categorical and numerical data.

  • What is categorical data and can you provide an example?

    -Categorical data describes categories or groups. An example given in the script is car brands like Mercedes, BMW, and Audi, which represent different categories.

  • How are yes and no questions related to categorical data?

    -Yes and no questions provide categorical data because they yield responses that can be grouped into two distinct categories: yes and no.

  • What is numerical data and how is it categorized further?

    -Numerical data represents numbers and is further divided into two subsets: discrete and continuous data.

  • Can you explain discrete data with an example from the script?

    -Discrete data can usually be counted in a finite manner. An example from the script is the number of children one wants to have, which is an integer value such as 0, 1, 2, or 10.

  • What is the significance of SAT exam grades in explaining discrete data?

    -SAT exam grades are used to illustrate discrete data because they are whole numbers (e.g., 1000, 1560, 1570, 2400) that can be imagined as separate members of a dataset with 10-point intervals.

  • How is continuous data different from discrete data?

    -Continuous data is infinite and impossible to count, unlike discrete data which is finite and can be counted. Continuous data can take on an infinite amount of values within a range.

  • Can you provide an example of continuous data from the script?

    -An example of continuous data from the script is weight, which can take on any value within a range and can vary by incomprehensibly small amounts.

  • Why are university grades considered discrete data?

    -University grades are considered discrete data because they typically take on integer values (A, B, C, D, E, F) or specific percentages (0 to 100 percent), not fractions or decimals.

  • How does the script differentiate between discrete and continuous money?

    -The script differentiates by stating that while money can be considered both discrete and continuous, physical money like banknotes and coins is discrete because you can't pay with fractions of a cent, such as $1.243.

  • What are some other examples of continuous data mentioned in the script?

    -Other examples of continuous data mentioned in the script include height, area, distance, and time, all of which can vary by infinitely smaller amounts.

  • Why is time on a clock considered discrete, while time in general is not?

    -Time on a clock is considered discrete because it is measured in fixed intervals (e.g., seconds, minutes). However, time in general is continuous as it can be measured with infinite precision, such as 72.123456 seconds.

Outlines
00:00
📊 Data Types: Categorical and Numerical

The script introduces two main types of data: categorical and numerical. Categorical data is used to describe categories or groups, such as car brands or yes/no answers. Numerical data, which represents numbers, is further divided into discrete and continuous subsets. Discrete data includes countable, finite values like the number of children one wants to have or SAT scores, which are integers. Continuous data, on the other hand, represents infinite values like weight, which can vary by infinitesimally small amounts. Examples of discrete data include university grades and the number of objects, while continuous data includes measurements like height, area, distance, and time, which can theoretically take on any value.

Mindmap
Keywords
💡Categorical Data
Categorical data refers to variables that are used to classify observations into groups. In the context of the video, car brands like Mercedes, BMW, and Audi are used as examples to illustrate how categorical data can represent different categories or groups. This type of data is essential for understanding the theme of data classification and is fundamental in statistics and data analysis.
💡Numerical Data
Numerical data is a type of data that consists of numerical values, which can be used to perform mathematical operations. The video script explains that numerical data is divided into discrete and continuous subsets, which is a key concept for understanding the nature of numerical data and its applications in various fields such as economics, science, and engineering.
💡Discrete Data
Discrete data is a subset of numerical data that can be counted and is finite in number. The video provides the example of the number of children someone might want to have, which is an integer value. This concept is crucial for understanding how certain numerical data can be counted and represented in whole numbers, which is a fundamental aspect of data analysis.
💡Continuous Data
Continuous data, as explained in the video, is infinite and can take on any value within a range. The example of weight is used to illustrate this concept, where weight can be measured with infinite precision, such as 150.01 pounds. This is a key concept in understanding how some numerical data can vary in infinitesimally small amounts and is essential for grasping the nature of real-world measurements.
💡Yes/No Questions
Yes/no questions are a form of categorical data where the response can only be one of two categories: yes or no. The video uses questions like 'Are you currently enrolled in a university?' and 'Do you own a car?' to demonstrate this concept. This is an important aspect of categorical data, showing how simple binary choices can be classified.
💡SAT Exam
The SAT exam is mentioned in the video as an example of discrete data, where scores are counted in specific increments, such as 10 points. This example is used to illustrate the concept of discrete numerical data and how it can be applied in educational testing, which is a context familiar to many viewers.
💡University Grades
University grades are given as an example of discrete data in the video, with letter grades (A, B, C, D, E, F) or percentage scores (0 to 100 percent). This example helps to clarify how educational performance can be quantified in discrete units, which is a common practice in academic settings.
💡Integer Values
Integer values are whole numbers that can be used to represent discrete data. The video mentions that the number of objects, such as bottles, glasses, tables, or cars, can only take integer values. This concept is fundamental to understanding discrete data and its application in counting objects.
💡Physical Money
Physical money, such as banknotes and coins, is used in the video to illustrate the concept of discrete data. It is mentioned that you can't pay with $1.243, but rather in increments such as $1.24, showing that money in physical form is discrete. This example helps to explain the concept of discrete numerical data in a financial context.
💡Height, Area, Distance, Time
These four measurements are given as examples of continuous data in the video. They can vary by infinitely small amounts and are incomprehensible for human measurement without technology. The video uses these examples to emphasize the infinite variability of continuous data, which is a key concept in understanding the nature of real-world measurements beyond simple counting.
Highlights

Introduction of data types: categorical and numerical data.

Categorical data describes categories or groups, such as car brands.

Examples of categorical data include yes/no answers to questions.

Numerical data represents numbers and is divided into discrete and continuous subsets.

Discrete data is finite and can be counted, such as the number of children one wants to have.

SAT exam grades are an example of discrete data with specific scoring increments.

Continuous data is infinite and can take on any value within a range, like weight.

Weight as an example of continuous data, with the potential for infinite decimal places.

The concept of discrete data as the opposite of continuous data.

Examples of discrete data include university grades and the count of objects.

Physical money is discrete due to its smallest denomination being a cent.

Continuous data examples include height, area, distance, and time.

Technology limits our measurement of continuous variables like weight and height.

Time can be considered continuous, with the ability to have infinite decimal precision.

Summary of the types of data and their characteristics.

Transcripts

Browse More Related Video

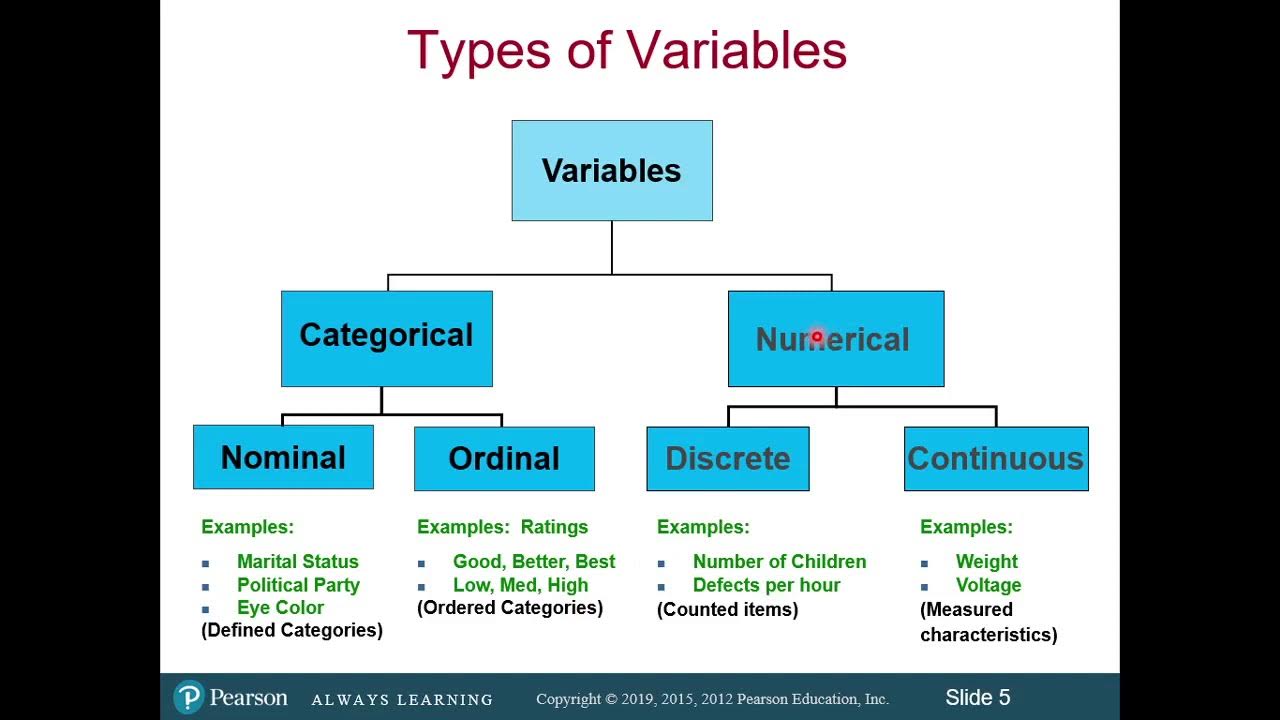
Classification of Variables and Types of Measurement Scales

Discrete v/s Continuous Data - What ? How ? || Discrete Data || Continuous Data || Basic Statistics

Variables and Types of Variables | Statistics Tutorial | MarinStatsLectures

Qualitative and Quantitative Data

Continuous vs Discrete Data

Discrete and continuous random variables | Probability and Statistics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Data TypesCategorical DataNumerical DataDiscrete ValuesContinuous ValuesData AnalysisEducationalStatistical ConceptsData ScienceData Measurement