Lesson 16 - Sequences (Calculus 2 Tutor)

Math and Science
18 Aug 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces the topic of sequences and series, which are often challenging for students studying calculus. The instructor emphasizes that sequences are simply lists of numbers, and they can be finite or infinite. The script explains the notation for sequences, using subscripts and curly braces, and highlights that sequences are not mathematically intensive like other calculus topics. The focus is on understanding definitions and memorizing key concepts to succeed in this area of calculus. The instructor assures viewers that by the end of several upcoming sections, they will become proficient in understanding and working with sequences and series.

Takeaways
  • 📚 The video is part of an advanced calculus tutorial series focusing on sequences and series, which are often challenging topics in calculus.
  • 🎯 The upcoming sections will progressively build upon each concept, aiming to make the audience proficient in understanding sequences and series.
  • 🔑 A sequence is fundamentally a list of numbers, which can be finite or infinite in length.
  • 📝 The general term in a sequence is denoted as \( a_n \), where 'n' represents the position of the term in the sequence.
  • 📘 The sequence can be written in shorthand notation using curly braces, for example, \( \{a_n\} \), to indicate a list of terms.
  • 📑 The shorthand notation can also include limits to specify the sequence's range, such as \( \{a_n\} \) where \( n = 1 \) to infinity.
  • 📈 The tutorial emphasizes that sequences and series are less mathematically intensive compared to other calculus topics like integration.
  • 📋 The importance of understanding definitions and committing them to memory is highlighted for success in tests and problem-solving.
  • 📈 The tutorial promises a structured approach to learning, breaking down complex concepts into more digestible parts.
  • 📚 The numbers in a sequence can be any type of number, including positive, negative, fractions, or decimals.
  • 📝 The tutorial is designed to make the audience comfortable with the foundational concept of sequences before moving on to series.
Q & A

  • What are the main topics covered in the upcoming sections of the advanced calculus tutorial?

    -The main topics covered are sequences and series, which are often challenging for many students in calculus.

  • Why are sequences and series considered challenging in calculus?

    -Sequences and series can be challenging because they require understanding definitions and committing some concepts to memory, rather than just performing complex calculations.

  • What is a sequence in the context of this tutorial?

    -A sequence is a list of numbers, which can be finite or infinite, and is denoted by terms like a1, a2, a3, ..., or a_n.

  • How can a sequence be represented in shorthand notation?

    -A sequence can be represented in shorthand notation using a curly brace with a subscript, like {a_n}, indicating that there are n elements in the sequence.

  • What does the subscript 'n' in the sequence notation {a_n} signify?

    -The subscript 'n' in {a_n} signifies that the sequence has n elements, where each element is represented by a term a_n.

  • Can the sequence be written with limits to indicate its infinite nature?

    -Yes, a sequence can be written with limits like {a_n} where n equals 1 to infinity, indicating that the sequence is infinite.

  • What is the difference between the terms 'terms' and 'elements' in the context of sequences?

    -In the context of sequences, 'terms' and 'elements' are used interchangeably to refer to the individual numbers in the sequence.

  • How does the tutorial plan to make the learning of sequences and series easier for students?

    -The tutorial plans to break down the concepts into natural, manageable chunks and build upon one concept at a time, making it easier for students to understand and remember.

  • What is the significance of understanding definitions in learning about sequences and series?

    -Understanding definitions is crucial because it helps students to grasp the fundamental concepts, which is essential for solving problems and doing well on tests.

  • What type of mathematical operations are NOT typically involved with sequences?

    -Sequences do not typically involve operations such as addition, subtraction, multiplication, or division among their terms.

  • How does the tutorial describe the complexity of sequences and series compared to other calculus topics?

    -The tutorial describes sequences and series as less mathematically intensive compared to other calculus topics like derivatives, integrals, and trigonometric identities.

Outlines
00:00
📚 Introduction to Sequences in Calculus

This paragraph introduces the topic of sequences and series, which are often challenging for students studying calculus. The instructor emphasizes that sequences are simply lists of numbers and are not as mathematically intensive as other calculus topics like derivatives and integrals. The focus of this section is on understanding the definitions and committing them to memory, as this is crucial for success in tests and further studies. The instructor also explains the notation used for sequences, such as using a subscript 'n' to denote the nth term (a_n), and the shorthand notation using curly braces to represent the sequence.

Mindmap
Keywords
💡Sequences
A sequence is defined as a list of numbers arranged in a specific order. This concept is foundational in calculus, particularly in the study of series and sequences. In the video, the sequence is described as a list that can contain any number of elements, which could be finite or infinite, and these elements are denoted as a1, a2, a3, etc.
💡Series
A series is the sum of the elements of a sequence. While the video mainly introduces sequences, it also mentions that understanding sequences is crucial for later tackling series. Series can involve summing an infinite number of terms, making it a critical concept in calculus.
💡Terms
Terms refer to the individual elements within a sequence. In the video, these are denoted as a1, a2, a3, and so on. Understanding each term's position and value within the sequence is essential for comprehending the overall structure of sequences and series.
💡Infinite
Infinite refers to sequences or series that do not have a finite number of terms. In the video, the instructor explains that sequences can have an infinite number of elements, which is a concept that can complicate calculations but is fundamental in advanced calculus.
💡Notation
Notation in mathematics provides a symbolic way to represent sequences and series. The video introduces the shorthand notation using curly braces to denote sequences, such as {a_n} where 'n' is the number of elements in the sequence. This helps in simplifying and clearly communicating complex mathematical ideas.
💡List of Numbers
A sequence is simply a list of numbers. This fundamental definition helps demystify the concept, making it accessible. The video emphasizes that this list can contain any type of numbers, including integers, fractions, and decimals.
💡Shorthand Notation
Shorthand notation is a concise way to represent sequences. In the video, curly braces and the notation a_n are used to simplify the representation of sequences. This notation is crucial for efficiently working with long or complex sequences.
💡Memory
Memory in this context refers to the necessity of remembering definitions and concepts related to sequences and series. The video highlights that committing these basics to memory is essential for success in calculus, as these foundational ideas are built upon in more complex topics.
💡Calculus
Calculus is the branch of mathematics that deals with continuous change, through concepts such as derivatives and integrals. The video situates sequences and series within this broader field, noting that while these topics may be less intensive than others, they are still fundamental to understanding calculus.
💡Elements
Elements are the individual numbers that make up a sequence. The video uses this term interchangeably with 'terms' and stresses that understanding each element's role is key to mastering sequences. Elements can be simple or complex, depending on the sequence.
Highlights

Introduction to the topic of sequences and series in advanced calculus.

Sequences and series can be challenging topics for many students.

The tutor plans to cover sequences and series in detail across multiple sections.

Building upon concepts gradually to make understanding sequences and series easier.

Sequences are fundamentally a list of numbers.

Contrasting sequences with more complex calculus concepts like derivatives and integrals.

Sequences and series are less mathematically intensive than other calculus topics.

Emphasis on understanding definitions and committing them to memory for sequences and series.

The importance of memorizing key concepts to succeed in tests.

Sequences can contain any number of elements, finite or infinite.

Denoting sequence elements as a1, a2, a3, ... an, or a_sub_n.

Using commas to separate sequence elements, indicating a list rather than an operation.

Shorthand notation for sequences using curly braces and a_sub_n.

Alternative shorthand notation including the limits n=1 to infinity.

Clarification that curly braces signify the start of a sequence notation.

Sequences consist of numbers that can be negative, positive, fractions, or decimals.

Transcripts

Browse More Related Video

Lesson 18 - Integral Test (Calculus 2 Tutor)

Ch. 12.1 Sequences and Summation Notation

Explicit and recursive definitions of sequences | Precalculus | Khan Academy

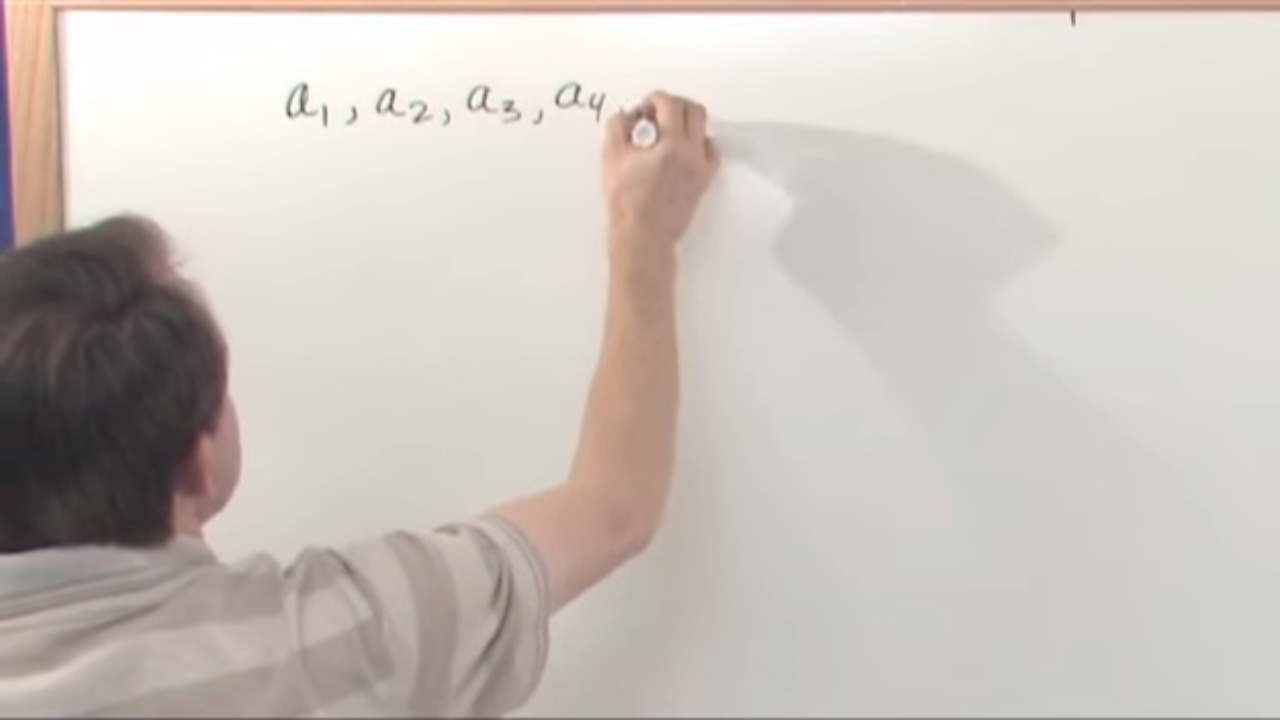
Lesson 17 - Series (Calculus 2 Tutor)

Convergence and Divergence: The Return of Sequences and Series

Arithmetic Sequences (Precalculus - College Algebra 69)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Advanced CalculusMath TutorialSequencesSeriesTrigonometryIntegralsDerivativesEducationalConceptualMathematical AnalysisProblem Solving