Finding Z-score Given Area - TI-84

Math and Stats Help
31 May 201709:29
EducationalLearning
32 Likes 10 Comments

TLDRThis instructional video tutorial guides viewers on how to calculate the z-score for a given area using a TI-84 calculator, which is applicable to TI-83 models as well. The presenter explains the process of finding the z-score by using the inverse norm function, taking into account whether the area is to the left, center, or right of the distribution. The video highlights a new feature on the TI-84 Plus CE that allows for easier calculation of both left and right tails. The tutorial also covers scenarios for finding z-scores for areas to the right and for areas in between, emphasizing the importance of using technology for precision beyond what standard tables can provide.

Takeaways
  • 📚 The video tutorial focuses on finding the z-score corresponding to a given area using a TI-84 calculator.
  • 🔢 It mentions that the process is similar for a TI-83 calculator, and there's another video for the TI-Nspire and a table method.
  • 🔍 The TI-84 calculator is used to find the inverse norm, which is the opposite of finding the area under the standard normal curve.
  • 📉 Most graphing calculators provide the area to the left of the z-score only.
  • 📱 The newest TI-84 Plus CE has additional features, such as options for left, center, and right tails, which are not available in older models.
  • 📝 To find the z-score, input the desired area, mean (usually 0 for standard normal distribution), and standard deviation (1 for standard normal distribution).
  • 📊 For areas to the left, use the inverse norm directly with the given area, mean, and standard deviation.
  • ➗ For areas to the right, use 1 minus the given area in the inverse norm function.
  • 🔄 For finding z-scores for an area in between, calculate half of the unshaded area (1 minus the desired area) to find the area to the left of the negative z-score.
  • 📌 The calculator will provide the z-score to two decimal places, which matches standard normal table values.
  • 🔎 If the calculator has the left, center, right feature, it simplifies finding z-scores for both tails and the area in between.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is to demonstrate how to find the z-score corresponding to a given area using a TI-84 calculator.

  • Is the process shown in the video applicable to TI-83 calculators as well?

    -Yes, the process shown for finding the z-score using the TI-84 calculator can also be applied to TI-83 calculators.

  • What is the significance of the term 'inverse norm' in the context of the video?

    -The term 'inverse norm' refers to the function on the calculator used to find the z-score when given an area under the standard normal distribution curve.

  • What feature does the TI-84 Plus CE have that not all graphing calculators have?

    -The TI-84 Plus CE has a feature that allows users to calculate the area to the left, center, or right of a z-score, which is not available in all graphing calculators.

  • How does the video explain finding the z-score for an area to the left?

    -The video explains that for an area to the left, you input the given area, mean (0 for standard normal), and standard deviation (1 for standard normal) into the inverse norm function on the calculator.

  • What is the standard mean and standard deviation used for the standard normal distribution?

    -The standard mean used for the standard normal distribution is 0, and the standard deviation is 1.

  • How does the video handle finding the z-score for an area to the right?

    -For an area to the right, the video instructs to use the inverse norm function and input 1 minus the given area, with the mean and standard deviation remaining 0 and 1, respectively.

  • What is the default setting for most graphing calculators regarding the area calculation?

    -The default setting for most graphing calculators is to calculate the area to the left of the z-score.

  • How does the video suggest finding z-scores for an area in between two z-scores?

    -The video suggests finding the area to the left of the negative z-score or the positive z-score, and then using half of the remaining area (1 minus the given area) to find the z-scores for the area in between.

  • What does the video recommend for rounding z-scores?

    -The video recommends rounding z-scores to two decimal places, which is the typical precision provided by standard normal distribution tables.

  • How does the video describe the advantage of using technology over tables for finding z-scores?

    -The video describes that technology, such as graphing calculators, can provide more precise z-scores with additional decimal places beyond what standard tables typically offer.

Outlines
00:00
📚 Finding the Z-Score Using TI-84 Calculator

This paragraph introduces the video's purpose, which is to demonstrate how to find the z-score corresponding to a given area using a TI-84 calculator. It mentions that the method is also applicable to TI-83 calculators. The video will use the inverse norm function, specific to the TI-84 Plus CE model, to find the z-score for a standard normal distribution with a mean of 0 and a standard deviation of 1. The area to the left is calculated, and the process is explained step by step, including navigating the calculator's menu and entering the necessary values. The TI-84 Plus CE's unique feature of selecting the area to the left, center, or right is highlighted, and viewers are guided through the process of finding the z-score for an area of 0.1562.

05:01
🔍 Calculating Z-Scores for Different Areas Using Advanced Features

The second paragraph continues the tutorial by explaining how to find z-scores for areas to the right and for areas in between using the TI-84 calculator. It clarifies that most calculators only provide the area to the left, so for areas to the right, the inverse norm function is used with 1 minus the given area. The process is demonstrated with an example where the z-score for an area of 0.1762 to the right is calculated, resulting in a z-score of approximately 0.93. The paragraph also addresses how to find z-scores for an area in between two z-scores, such as 86%, by finding the area to the left of the negative z-score and dividing it by two. The TI-84 Plus CE's advanced feature that simplifies finding both the left and right z-scores is mentioned, and the default process for calculators without this feature is explained. The video concludes with a demonstration of how to find the z-scores for an 86% area in between using the inverse norm function with the center option on the TI-84 Plus CE.

Mindmap
Keywords
💡z-score
A z-score is a statistical measurement that indicates how many standard deviations an element is from the mean. In the context of the video, finding the z-score is the primary objective, as it helps in determining the value that corresponds to a given area under the standard normal distribution curve. The script mentions that the z-score is always associated with the standard normal table, which has a mean of 0 and a standard deviation of 1.
💡TI-84
The TI-84 is a graphing calculator produced by Texas Instruments, widely used in educational settings for various mathematical computations. The video specifically focuses on how to use the TI-84 calculator to find z-scores. It is noted that the process would be similar for the TI-83 model as well.
💡area under the curve
In statistics, the area under the curve refers to the proportion of data points that fall within a certain range in a probability distribution. The video script discusses finding the z-score that corresponds to a specific area, such as 0.1562, which represents the probability or the area under the standard normal curve to the left of that z-score.
💡inverse norm
The inverse norm, as mentioned in the video, is a function on graphing calculators that calculates the inverse of the cumulative distribution function for the standard normal distribution. It is used to find the z-score when the area under the curve (probability) is known.
💡mean
The mean, often referred to as the average, is a measure of central tendency in a set of numbers. In the script, the mean is discussed in the context of the standard normal distribution, which has a mean of 0. This is important when calculating z-scores because it is part of the standardization process.
💡standard deviation
Standard deviation is a measure that indicates the amount of variation or dispersion in a set of values. In the video, the standard deviation is noted as being 1 for the standard normal distribution, which is a key component in the calculation of z-scores.
💡left tail
The term 'left tail' in the context of the video refers to the area under the standard normal curve to the left of a specified z-score. The script explains that most graphing calculators, including the TI-84, are programmed to calculate the area to the left by default.
💡right tail
Conversely, the 'right tail' refers to the area under the curve to the right of a specified z-score. The video demonstrates how to calculate the z-score for an area to the right by using the inverse norm function and adjusting the input area accordingly.
💡center
The 'center' in the context of the video refers to the area between two z-scores, which is not directly calculated by most graphing calculators. However, the script explains that newer models of the TI-84 have an option to calculate this area, simplifying the process.
💡decimal places
Decimal places are the digits to the right of the decimal point in a number. The video mentions rounding z-scores to two decimal places for simplicity, but also notes that technology can provide more precise values beyond two decimal places if needed.
Highlights

The video demonstrates how to find the z-score corresponding to a given area using a TI-84 calculator.

A TI-83 calculator can also be used in the same way as the TI-84 for this process.

The method involves using the inverse norm function on the calculator.

Most graphing calculators provide the area to the left only.

The TI-84 Plus CE has unique features not present in all graphing calculators.

For finding the z-score, the calculator requires the area, mean, and standard deviation.

The standard normal table has a mean of 0 and a standard deviation of 1.

The calculator's 'distributions' menu option 3 is used to access the inverse norm function.

Some calculators have options for left, center, and right tails, but most default to the left.

The area to the left is entered as 0.1562 for the example given.

The calculator provides the z-score to two decimal places, similar to a standard normal table.

For areas to the right, the calculator requires 1 minus the given area to find the z-score.

Technology can provide more decimal places than a standard normal table.

For areas between two z-scores, the calculator can find both the negative and positive z-scores.

If the calculator has a 'center' option, it simplifies finding z-scores for areas between two values.

The default method for most calculators is to find the area to the left of a z-score.

The video concludes with a reminder of the practical applications of the process shown.

Transcripts

Browse More Related Video

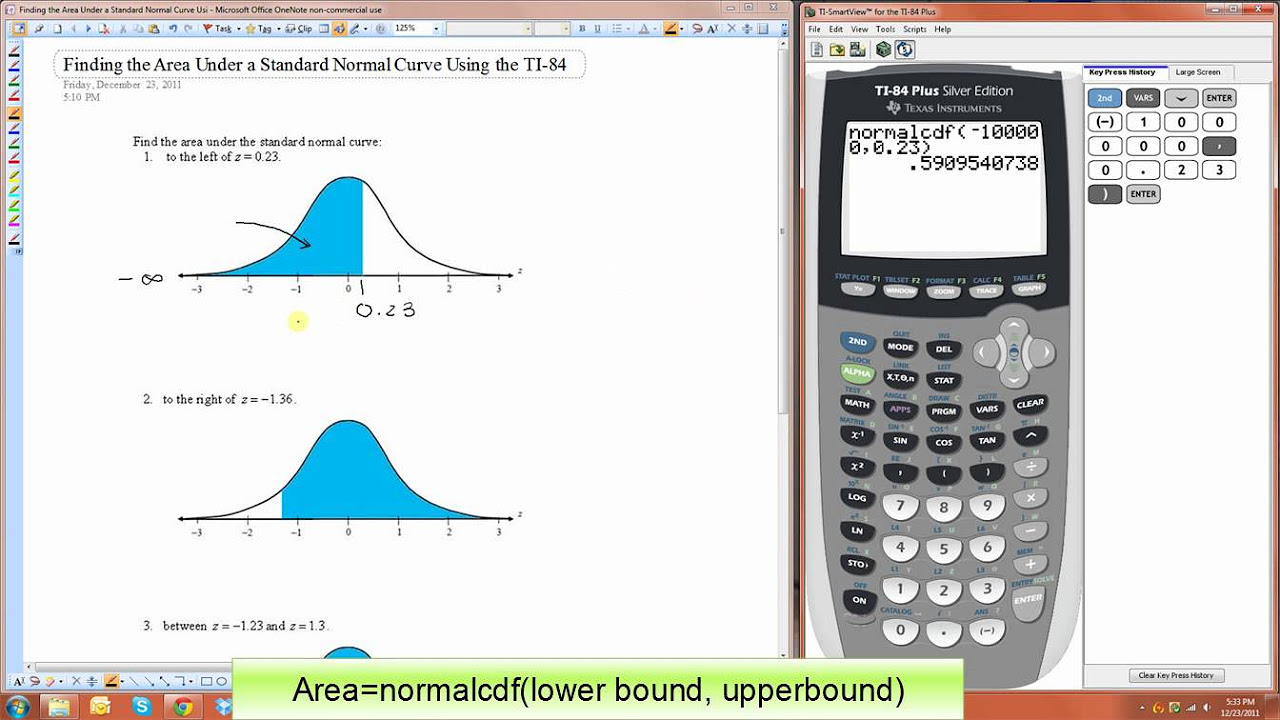
Finding the Area Under a Standard Normal Curve Using the TI-84

Normal Distribution: Calculating Quantiles {TI 84 Plus CE}

6.1.4 The Standard Normal Distribution - Given a range of z scores, find areas or probabilities.

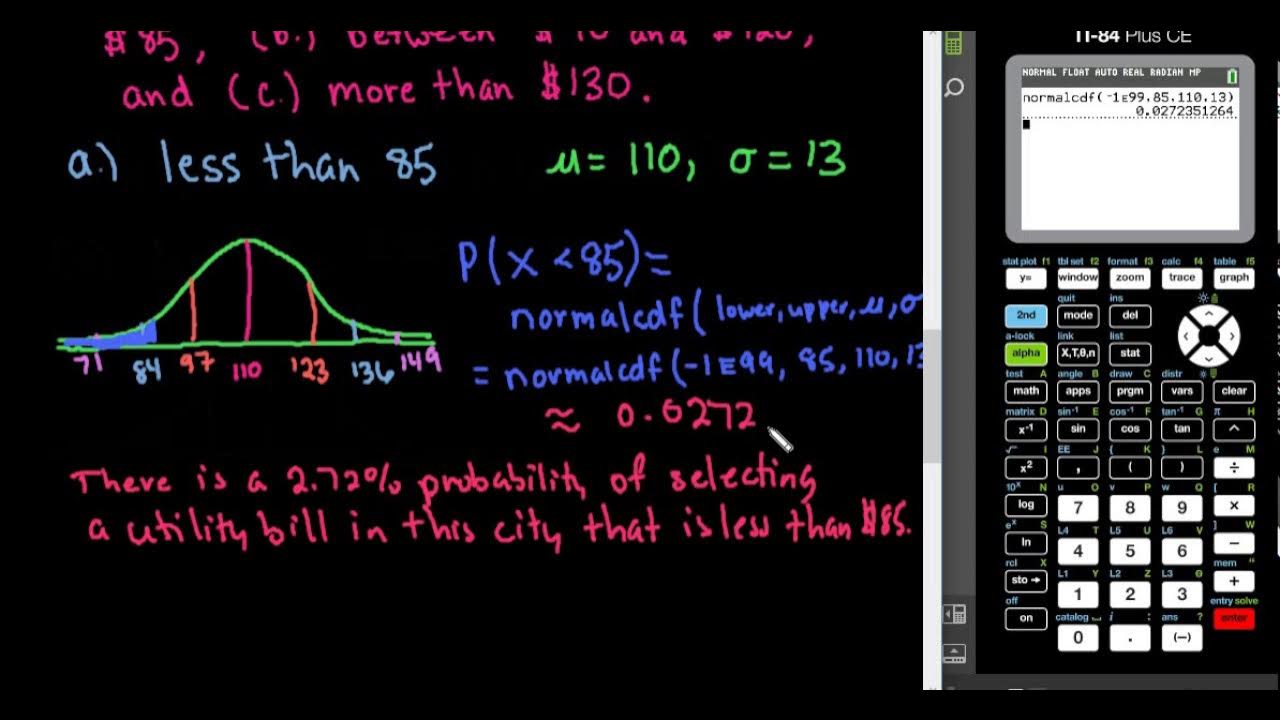
Probabilities in a Normal Distribution - TI-84

Find the z-score given the confidence level

Which TI-84 Plus is Best for You? Reviewing Every TI-84 Plus (CE)!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Z-Score CalculationTI-84 TutorialStandard NormalGraphing CalculatorStatistical AnalysisArea to LeftInverse NormMean & SDProbability TheoryEducational ContentMathematics Tutorial