Calculus - Lesson 5 | What are Functions? | Don't Memorise
TLDRThis educational video script explores the concept of functions in a relatable way, starting with the analogy of a plant's shadow to explain how the length of a shadow is a function of the position of the light source and the height of the plant. It then transitions into the mathematical realm, discussing how functions work in calculus, particularly the use of limits to find instantaneous speed. The script uses a car's motion to illustrate the idea of a function representing the relationship between time and distance, and how differentiation can reveal the rate of change, such as speed. It concludes by highlighting the versatility of functions, showing how the same mathematical relationship can model different real-world scenarios, like the area of a square being a function of its side length.
Takeaways
- 🌞 The length of a shadow is dependent on the position of the light source and the height of the object.
- 📏 Understanding functions can be simplified by considering inputs (light source position, object height) and outputs (shadow length).
- 🔍 In calculus, functions are used to find instantaneous rates like speed at a specific instant, which is the limit of average speed as time intervals approach zero.
- 🚗 To find the speed at an instant, average speeds over smaller and smaller time intervals are calculated until they converge to a single value.
- 📉 The concept of limits is crucial to ensure that the average speed does not approach an incorrect value but rather a specific number, like 40 in the example.
- 📚 A mathematical relationship between time and distance can be very powerful in determining the speed at any given instant.
- 📉 The average speed can be represented algebraically, showing how it approaches a certain value as the time interval approaches zero.
- 🔑 The relationship between time and distance is an example of a function, where for every value of time, there is a corresponding value of distance.
- 📐 The concept of functions is not limited to motion; it can also describe other relationships, such as the area of a square being a function of its side length.
- 🔄 Differentiation in calculus allows us to derive a new function that represents the rate of change, such as speed being the derivative of distance with respect to time.
- 🔍 The same mathematical equation can represent different functions depending on the context, such as time and distance or side length and area.
Q & A
What determines the length of a shadow cast by a plant?
-The length of a shadow is dependent on two main factors: the position of the source of light and the height of the plant.
How is the concept of a function introduced in the script?
-The concept of a function is introduced by explaining that the output (length of the shadow) is dependent on certain inputs (position of light source and height of the plant), which is a simple way to understand functions.
What is the role of limits in finding the instantaneous speed of an object?
-Limits are used to find the instantaneous speed of an object by taking the average speed over smaller and smaller time intervals, approaching the specific instant in question.
How can we be confident that the average speed approaches a specific number at an instant?
-We can be confident by finding average speeds at even closer time intervals, thus narrowing down the range of possible values and approaching the exact speed at that instant.
What information do we need to find the speed at an instant according to the script?
-To find the speed at an instant, we need to know the distance traveled by the object in various time intervals very close to that instant.
How does the script illustrate the relationship between distance and time for a moving object?
-The script uses a mathematical relation where distance traveled is represented as a function of time, showing how knowing this relationship can help determine the speed at any instant.
What is the significance of the variable 'h' in the context of the script?
-In the script, 'h' signifies a small duration of time after a specific time point. As 'h' approaches zero, it helps in calculating the average speed over smaller time intervals, leading to the instantaneous speed.
How does the script relate the concept of functions to the motion of an object?
-The script relates the concept of functions to the motion of an object by explaining that the distance traveled by an object is a function of time elapsed, with each value of time having a corresponding value of distance.
What is the role of differentiation in the context of functions as described in the script?
-Differentiation is used to find the rate of change of one variable with respect to another. In the context of the script, it helps in determining the speed of an object (rate of change of distance with respect to time) from the distance-time function.
How does the script use the example of a square to explain functions?
-The script uses the example of a square to explain that the area of the square is a function of the length of its side, where the length is the independent variable and the area is the dependent variable.
What does the script suggest about the versatility of functions?
-The script suggests that functions are versatile by showing that the same mathematical equation can represent different relationships, such as the distance-time relation for an object in motion and the side-area relation for a square.
Outlines
🌳 Understanding Shadows and Functions
This paragraph explores the concept of functions using the analogy of a plant's shadow. It explains that the length of the shadow is dependent on two factors: the position of the light source and the height of the plant. The paragraph introduces functions as a relationship where the output (shadow length) is determined by specific inputs (light source position and plant height). It also touches on the idea of instantaneous speed in calculus, using limits to find the speed of an object at a particular instant by taking average speeds over increasingly smaller time intervals. The paragraph concludes by asking viewers to consider additional inputs that might affect the shadow's length and to ponder how functions operate within the realm of calculus.
🚗 Instantaneous Speed and the Power of Mathematical Relationships
The second paragraph delves into the mathematical representation of motion, specifically the relationship between time, distance, and speed. It uses the formula for distance traveled by an object to illustrate how knowing this relationship allows us to calculate the instantaneous speed at any given time. The paragraph explains the process of differentiation to derive the speed function from the distance-time relationship and highlights the historical significance of this concept, credited to Galileo's discovery that freely falling objects follow a specific mathematical pattern. It also demonstrates how the same mathematical equation can represent different functions, such as the area of a square being a function of its side length, and introduces the notation commonly used to denote functions, distinguishing between independent and dependent variables.
📚 The Essence of Functions and Rate of Change
In the final paragraph, the focus shifts to the broader concept of functions and their role in determining the rate of change between variables. It emphasizes that a function is a definitive relationship where each value of the independent variable corresponds to a single value of the dependent variable. The paragraph illustrates this with the example of a square's area being a function of its side length and how differentiation provides the rate of change, whether it's the speed of an object or the change in area as the side length varies. It concludes by posing a question that connects the mathematical concept to real-world applications, such as flashlights or satellite dishes, and encourages viewers to share their thoughts in the comments section.
Mindmap
Keywords
💡Shadow
💡Function
💡Instantaneous Speed
💡Average Speed
💡Limits
💡Relation
💡Differentiation
💡Rate of Change
💡Independent Variable
💡Dependent Variable
💡Galileo
Highlights
The length of a shadow is dependent on the position of the source of light and the height of the plant.
Understanding functions through the simple example of a shadow's length being a function of light source position and plant height.
The concept of instantaneous speed of an object can be found using the idea of average speed and limits.
To find the speed at an instant, average speeds in very small time intervals near that position are considered.
The process of finding the exact speed at an instant involves narrowing down the range of possible speeds through closer time intervals.
Knowing the relationship between distance and time allows for the calculation of speed at any instant.
A mathematical representation of a function can be used to determine the speed of an object at any given time.
The speed of an object can be represented as a function of time, where each time value has a corresponding speed value.
Galileo's discovery that the speed of any freely falling object at any instant can be calculated using a specific relationship.
Different relationships for different speeds and accelerations can be represented by different equations.
The area of a square is a function of the length of its side, demonstrated through a simple equation.
The same mathematical equation can represent different functions, such as time and distance or side length and area.
Functions are denoted by symbols to distinguish between independent and dependent variables.
Differentiation is used to find the rate of change, such as speed, from a given function.
The concept of functions allows for the calculation of rates of change, such as the speed of an object or the change in area of a square.
The video invites viewers to explore the connection between the function example and everyday objects like a flashlight or a satellite dish.
The video concludes with an invitation to subscribe to the channel for more educational content.
Transcripts
Browse More Related Video
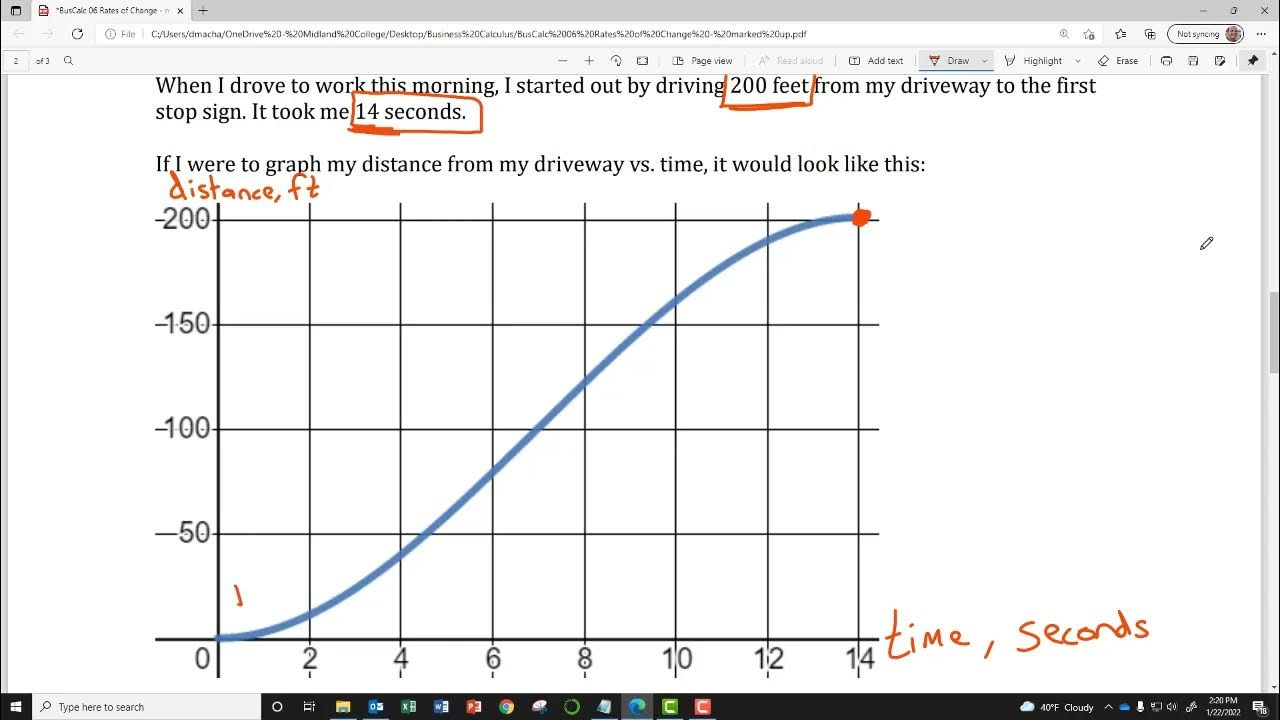
BusCalc 06 Rates of Change

Calculus | Derivatives of a Function - Lesson 7 | Don't Memorise
Moving Shadow Problem (Related Rates)

Calculus - Lesson 6 | What are Functions? | Don't Memorise

Area under rate function gives the net change | AP Calculus AB | Khan Academy
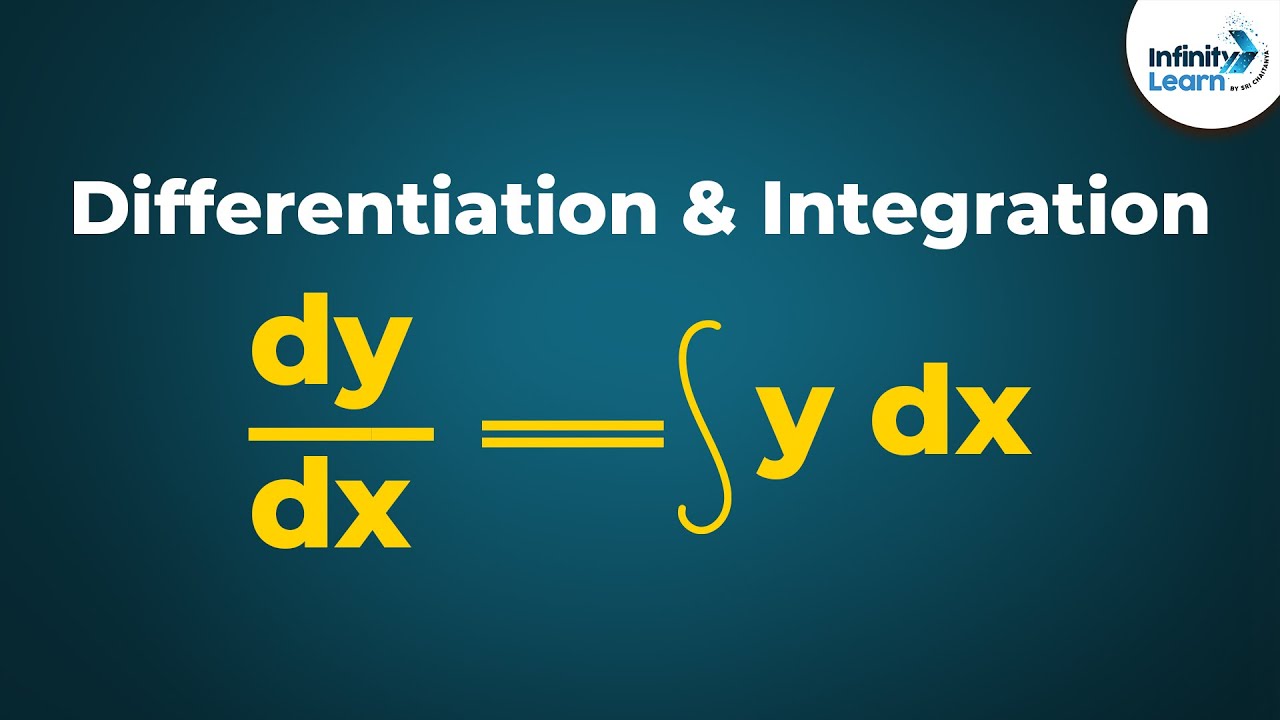
Calculus - Lesson 15 | Relation between Differentiation and Integration | Don't Memorise
5.0 / 5 (0 votes)
Thanks for rating: