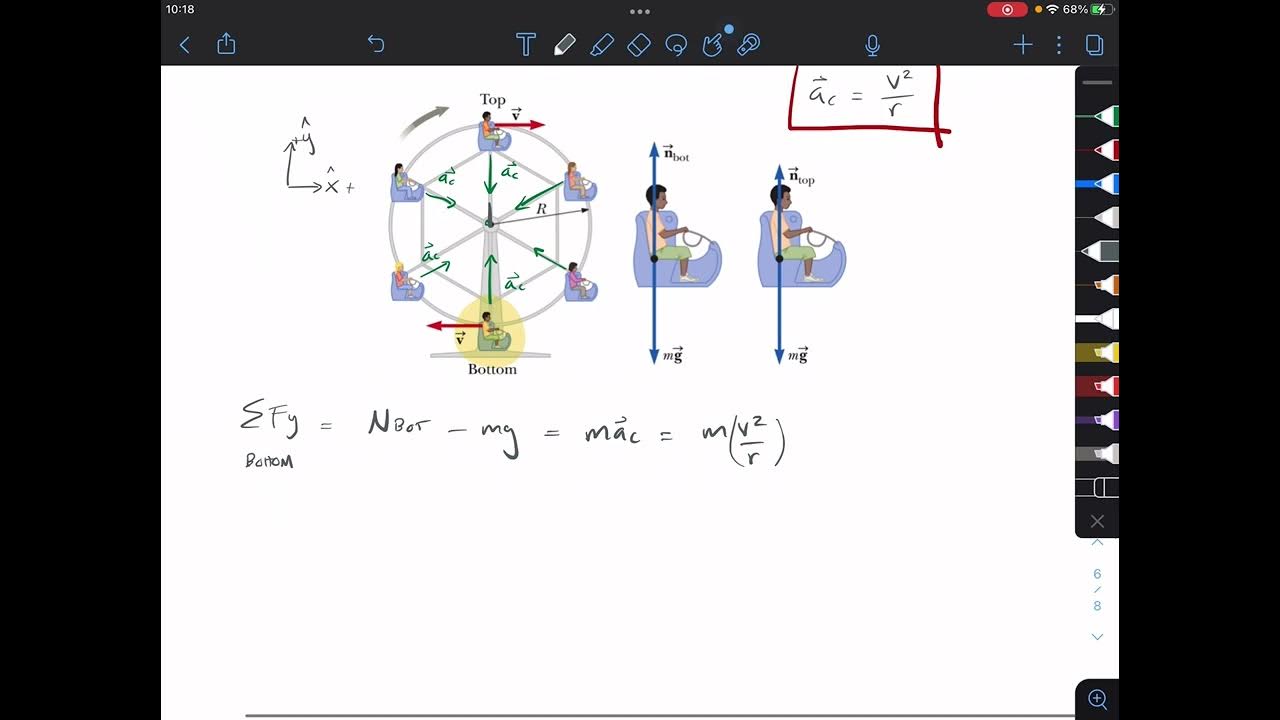
Normal Force on Ferris Wheel

Andrey K
8 Aug 201303:27
EducationalLearning
32 Likes 10 Comments

TLDRThe script explores the concept of normal force experienced by a person on a Ferris wheel at different points of the rotation. It explains that when at the top, the person's acceleration is downward due to gravity, while at the bottom, the acceleration is upward. By analyzing the forces acting on the person using a free body diagram, the script demonstrates that the normal force exerted by the seat is greater at the bottom of the arc compared to the top. This is due to the combination of gravitational force and the upward acceleration at the bottom, which requires a larger normal force to counteract.

Takeaways
  • 🎡 The scenario involves a person on a Ferris wheel that rotates with a constant rotational speed.
  • 🧭 At the top of the Ferris wheel, the person experiences a downward acceleration due to gravity and centripetal force.
  • 🔽 The gravitational force acts downward along the y-axis, while the normal force from the seat acts upward.
  • 🌐 The person's radial or centripetal acceleration at the top points downward, aligning with the gravitational force.
  • 🔼 At the bottom of the Ferris wheel, the person's acceleration is upward, opposite to the direction of gravity.
  • 📈 The normal force and gravitational force are the two main forces acting on the person along the y-axis.
  • ⚖️ The normal force is calculated by considering the balance of forces and the person's mass and acceleration.
  • 🔢 The equations for the forces at the top and bottom of the Ferris wheel are rearranged to solve for the normal force.
  • 📉 At the top of the arc, the normal force is the gravitational force minus the mass times the radial acceleration.
  • 📈 At the bottom of the arc, the normal force is the mass times the radial acceleration plus the gravitational force.
  • 🆚 The normal force exerted by the seat on the person is greater at the bottom of the arc compared to the top.
Q & A

  • What is the scenario described in the script?

    -The script describes a scenario where a person is on a Ferris wheel that rotates with a certain rotational speed, and the person's rotational speed matches that of the Ferris wheel.

  • What is the main question the script aims to answer?

    -The main question is whether the normal force exerted by the seat on the person is greater at the bottom or at the top of the Ferris wheel's arc.

  • What is a free body diagram?

    -A free body diagram is a graphical representation used to visualize all the forces acting on an object in a given situation, which helps in analyzing the forces and motion.

  • What are the two forces acting on the person at the top of the Ferris wheel?

    -At the top, the two forces acting on the person are the gravitational force pulling them downward and the normal force from the seat pushing them upward.

  • In what direction is the person accelerating at the top of the Ferris wheel?

    -At the top of the Ferris wheel, the person is accelerating directly downward, in the same direction as the gravitational force.

  • What changes when considering the forces at the bottom of the Ferris wheel?

    -At the bottom, the person is still subjected to the gravitational force pulling them downward and the normal force pushing them upward, but now they are accelerating upward due to their position in the arc.

  • Why is the direction of acceleration different at the bottom compared to the top?

    -The direction of acceleration changes because at the bottom of the arc, the person is moving away from the center of the Ferris wheel, thus experiencing an upward acceleration, whereas at the top, they are moving towards the center, resulting in downward acceleration.

  • How does the script define the positive direction for force calculations at the top and bottom?

    -At the top, the downward direction is chosen as positive, and at the bottom, the upward direction is chosen as positive for the force calculations.

  • What are the equations used to calculate the normal force at the top and bottom?

    -At the top, the equation is Normal Force = Gravitational Force - (mass × radial acceleration). At the bottom, it is Normal Force = (mass × radial acceleration) + Gravitational Force.

  • Why is the normal force greater at the bottom of the arc compared to the top?

    -The normal force is greater at the bottom because, in addition to the gravitational force, there is an upward acceleration due to the circular motion, which requires an additional upward force to counteract.

  • What would be the practical implication of knowing the normal force at different points on the Ferris wheel?

    -Knowing the normal force helps in understanding the physical experience of the person on the Ferris wheel, such as the feeling of weightlessness at the top and increased force at the bottom, and it's crucial for the structural design of the Ferris wheel to ensure safety.

Outlines
00:00
🎡 Understanding Normal Force in a Ferris Wheel

The script begins by setting the scene of a person inside a Ferris wheel and introduces a central question regarding the normal force exerted by the seat on the person at different points of the wheel's rotation. The paragraph explains that the normal force will vary depending on whether the person is at the top or bottom of the Ferris wheel's arc. It describes the forces acting on the person at both the top and bottom of the arc, including gravitational force and centripetal acceleration. The script then outlines the process of creating a free body diagram and force diagrams to analyze these forces. It concludes by rearranging equations to solve for the normal force, revealing that the normal force is greater at the bottom of the arc than at the top, which can be confirmed by plugging in specific numbers.

Mindmap
Keywords
💡Ferris Wheel
A Ferris wheel is a large vertical wheel with passenger cabins or seats attached around its circumference. In the context of the video, it serves as the central object of study to explore the effects of rotational motion on the forces acting on a person. The script discusses how a person's rotational speed matches that of the Ferris wheel, providing a real-world scenario to analyze the physics involved.
💡Rotational Speed
Rotational speed refers to the rate at which an object rotates around an axis, typically measured in revolutions per minute (RPM) or radians per second. In the video, the rotational speed is crucial as it determines the centripetal acceleration experienced by the person on the Ferris wheel, which in turn affects the normal force exerted by the seat.
💡Normal Force
The normal force is the perpendicular force exerted by a surface that supports the weight of an object resting on it. In the video, the normal force is the key variable being compared at the top and bottom of the Ferris wheel's arc. The script explains how this force changes due to the person's centripetal acceleration at different points on the wheel.
💡Centripetal Acceleration
Centripetal acceleration is the acceleration directed towards the center of a circular path that an object experiences when it is moving in a circle at a constant speed. The script uses this concept to explain why the normal force is different at the top and bottom of the Ferris wheel's arc, with the person accelerating downwards at the top and upwards at the bottom.
💡Free Body Diagram
A free body diagram is a simplified illustration that shows all the forces acting on an object in a particular situation. In the video, the script mentions examining the free body diagram to conceptualize the forces at play when the person is at the top and bottom of the Ferris wheel, which helps in understanding the dynamics of the situation.
💡Gravitational Force
Gravitational force is the attractive force that a body experiences due to the mass of objects around it, particularly the Earth's gravity pulling objects downwards. The script describes how gravitational force acts on the person in the Ferris wheel and how it interacts with the normal force to create different sensations at different points on the ride.
💡Radial Acceleration
Radial acceleration is the component of acceleration that acts along the radius of a circular path. In the context of the video, radial acceleration is synonymous with centripetal acceleration, and it is used to describe the direction and magnitude of the acceleration experienced by the person on the Ferris wheel.
💡Arc
An arc is a portion of the circumference of a circle or a curved line segment. In the video, the term 'arc' is used to describe the path followed by the person on the Ferris wheel, with a focus on the top and bottom points of the arc where the normal force is analyzed.
💡Positive Direction
Positive direction refers to the chosen direction for the purpose of analysis in physics problems, often arbitrarily selected for the sake of calculation. In the video, the script specifies the downward direction as positive at the top of the Ferris wheel and the upward direction as positive at the bottom, to simplify the force equations.
💡Equations of Motion
Equations of motion are mathematical equations that describe the relationship between the forces acting on an object and its motion. The script uses these equations to calculate the normal force at different points on the Ferris wheel, demonstrating how physics principles can be applied to real-world scenarios.
Highlights

Person's rotational speed matches the Ferris wheel's rotational speed.

Question posed: Is the normal force on the person greater at the bottom or top of the arc?

Conceptual examination of free body diagram required to answer the question.

Force diagrams at the top and bottom of the arc are analyzed.

At the top, two forces act along the y-axis: gravitational force and normal force.

Person's acceleration at the top is downward, aligning with gravitational force.

At the bottom, person's acceleration is upward due to arc's position.

Forces on the person along the y-axis are summed for both positions.

Downward direction is chosen as positive for the top position.

Upward direction is chosen as positive for the bottom position.

Equations rearranged to solve for the normal force in both cases.

Normal force at the bottom is calculated to be greater than at the top.

Numerical example would confirm the theoretical finding.

Theoretical contributions include understanding of centripetal acceleration.

Practical application could be in designing amusement park rides.

Impact on understanding the physics of rotational motion.

Engaging manner to summarize core content of rotational dynamics.

Transcripts

Browse More Related Video

Circular motion and apparent weight

Uniform Circular Motion - 3 - Ferris Wheel

Circular Motion: Ferris Wheel

AP Physics Workbook 3.E Maximum speed over the top

Uniform Circular Motion, Example #1 Ferris wheel

Roller coaster loop the loop

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Ferris WheelRotational SpeedNormal ForcePhysicsCentripetal ForceGravitational ForceAccelerationFree Body DiagramRadial AccelerationMechanical Motion