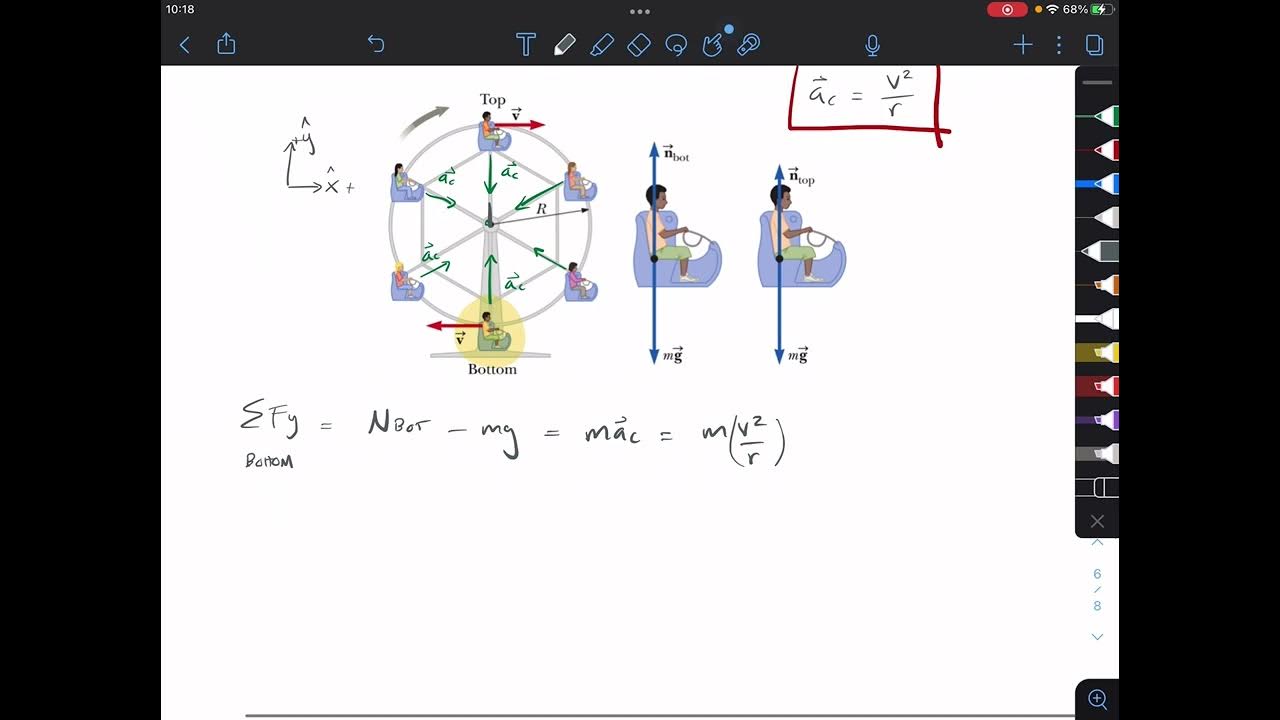
Uniform Circular Motion, Example #1 Ferris wheel

Ian Page
8 Oct 201905:02
EducationalLearning
32 Likes 10 Comments

TLDRIn this example, the presenter explains the motion of a woman on a Ferris wheel with a radius of 15 meters completing five turns in one minute. The tasks include calculating the period of the Ferris wheel, finding the centripetal acceleration at the highest and lowest points. The period is found to be 12 seconds. Using this, the centripetal acceleration at the top is calculated as 4.11 m/s^2 directed downward. At the bottom, the centripetal acceleration is also 4.11 m/s^2 but directed upward. The explanation emphasizes understanding the direction of acceleration in circular motion.

Takeaways
  • 🎑 The scenario involves a woman traveling in a Ferris wheel with a radius of 15 meters.
  • ⏱ The Ferris wheel completes five turns in one minute, which is used to calculate the period.
  • πŸ•’ The period (T) is the time for one complete revolution, calculated as 60 seconds divided by 5, resulting in 12 seconds.
  • πŸš€ In Part B, the centripetal acceleration at the top of the Ferris wheel is to be found using the formula velocity squared divided by radius.
  • πŸ“ The velocity is calculated as the distance around the circle (2Ο€R) divided by the period, yielding approximately 7.85 meters per second.
  • πŸ”’ The centripetal acceleration at the top is calculated to be 4.11 m/sΒ², directed downwards towards the center of the circle.
  • πŸ”„ The same equation is used to find the centripetal acceleration at the bottom of the Ferris wheel in Part C.
  • πŸ“‰ At the bottom, the magnitude of the centripetal acceleration remains 4.11 m/sΒ², but the direction is upwards, away from the center of the circle.
  • 🧭 The direction of centripetal acceleration is always towards the center of the circular path, changing based on the position (top or bottom).
  • πŸ“š The script explains the concept of centripetal acceleration and its calculation, emphasizing its directionality due to the changing position in a circular motion.
Q & A

  • What is the radius of the Ferris wheel mentioned in the script?

    -The radius of the Ferris wheel is given as 15 meters.

  • How many turns does the Ferris wheel complete in one minute?

    -The Ferris wheel completes five turns in one minute.

  • What is the period (T) of one complete revolution of the Ferris wheel?

    -The period (T) of one complete revolution is calculated to be 12 seconds.

  • What is the formula for calculating the centripetal acceleration at any point on the Ferris wheel?

    -The formula for centripetal acceleration is the velocity squared divided by the radius (a_c = v^2 / r).

  • How is the velocity of the woman on the Ferris wheel calculated?

    -The velocity is calculated by dividing the distance around the circle (2Ο€r) by the period (T).

  • What is the approximate velocity of the woman on the Ferris wheel?

    -The approximate velocity of the woman is 7.85 meters per second.

  • What is the centripetal acceleration at the highest point of the Ferris wheel?

    -The centripetal acceleration at the highest point is 4.11 meters per second squared, directed downwards.

  • What is the direction of the centripetal acceleration at the top of the Ferris wheel?

    -At the top of the Ferris wheel, the centripetal acceleration is directed downwards towards the center of the circle.

  • What is the centripetal acceleration at the lowest point of the Ferris wheel?

    -The centripetal acceleration at the lowest point is also 4.11 meters per second squared, but the direction is upwards.

  • What is the direction of the centripetal acceleration at the bottom of the Ferris wheel?

    -At the bottom of the Ferris wheel, the centripetal acceleration is directed upwards towards the center of the circle.

  • Why does the direction of centripetal acceleration change between the top and bottom of the Ferris wheel?

    -The direction of centripetal acceleration changes because it always points towards the center of the circle, which is vertically downward at the top and upward at the bottom.

  • How does the script illustrate the concept of centripetal force and acceleration?

    -The script uses the example of a woman on a Ferris wheel to illustrate how centripetal force and acceleration are calculated and directed towards the center of the circular path.

Outlines
00:00
🎑 Physics of a Ferris Wheel Ride

The script introduces a physics problem involving a woman on a Ferris wheel with a 15-meter radius. She completes five revolutions around a horizontal axis in one minute. The task is to calculate the period of rotation (Part A), the centripetal acceleration at the highest point (Part B), and at the lowest point (Part C). The period is determined to be 12 seconds by dividing the total time of one minute (60 seconds) by the number of turns (5). To find the centripetal acceleration, the script uses the formula which involves the velocity squared divided by the radius. The velocity is calculated by the distance traveled (2Ο€R) over the period. After calculating the velocity to be approximately 7.85 meters per second, the centripetal acceleration is found to be 4.11 m/sΒ², directed towards the center of the Ferris wheel. The direction of this acceleration changes depending on whether the woman is at the top or bottom of the wheel, with it being downward at the top and upward at the bottom.

Mindmap
Keywords
πŸ’‘Ferris Wheel
A Ferris wheel is a large vertical wheel with passenger cabins or seats attached around its circumference. In the video script, the Ferris wheel serves as the central example for explaining concepts related to circular motion. The woman traveling in the Ferris wheel completes five turns in one minute, which is used to calculate the period of rotation.
πŸ’‘Radius
The radius is the distance from the center of a circle to any point on its circumference. In the context of the video, the radius of the Ferris wheel is given as 15 meters, which is a key measurement used to calculate the period and centripetal acceleration.
πŸ’‘Period
The period (represented by a capital T) is the time taken for one complete cycle of a recurring event. In the video, the period is calculated by dividing the total time of one minute by the number of turns the Ferris wheel makes, which is five, resulting in a period of 12 seconds.
πŸ’‘Centripetal Acceleration
Centripetal acceleration is the acceleration directed towards the center of a circular path, experienced by an object moving in a circular motion. The script explains how to calculate this acceleration using the formula v^2/r, where v is the velocity and r is the radius. It is a central concept in the video, discussed in the context of both the highest and lowest points of the Ferris wheel.
πŸ’‘Velocity
Velocity is a vector quantity that refers to the rate of change of an object's position with respect to time, in a given direction. In the script, the velocity of the woman on the Ferris wheel is calculated by dividing the distance traveled (2Ο€R) by the period of rotation, which is essential for determining the centripetal acceleration.
πŸ’‘Horizontal Axis
The horizontal axis, in the context of the Ferris wheel, is the imaginary line around which the wheel rotates. The script mentions that the Ferris wheel rotates around its horizontal axis, which is important for understanding the direction of the centripetal acceleration.
πŸ’‘Highest Point
The highest point in the context of the Ferris wheel is the topmost position of the wheel's rotation. The script discusses the centripetal acceleration at this point, noting that it is directed downwards due to the woman's position at the top of the circular path.
πŸ’‘Lowest Point
The lowest point is the bottommost position of the Ferris wheel's rotation. The script explains that the magnitude of centripetal acceleration remains the same as at the highest point, but the direction changes to upwards, as the center of the circle is now above the woman.
πŸ’‘Turns
In the script, 'turns' refers to the number of complete rotations the Ferris wheel makes. The woman completes five turns in one minute, which is a key piece of information used to calculate the period and further physical quantities.
πŸ’‘Direction of Acceleration
The direction of acceleration is crucial in understanding the dynamics of circular motion. The script explains that at the highest point, the centripetal acceleration is downwards, while at the lowest point, it is upwards, illustrating how the direction changes with the position on the Ferris wheel.
Highlights

A woman is traveling in a Ferris wheel with a radius of 15 meters.

The Ferris wheel completes five turns in one minute.

Part A requires finding the period of the Ferris wheel's rotation.

The period is the time taken for one complete revolution.

The period is calculated as 60 seconds divided by 5, resulting in 12 seconds.

Part B asks for the centripetal acceleration at the highest point.

Centripetal acceleration is velocity squared divided by the radius.

Velocity is calculated as the distance around the circle divided by the period.

The calculated velocity is approximately 7.85 meters per second.

Centripetal acceleration at the top is 4.11 meters per second squared, directed downwards.

Part C requires finding the centripetal acceleration at the lowest point.

The same equation is used for centripetal acceleration at the bottom.

The acceleration at the bottom is also 4.11 m/s^2, but directed upwards.

The direction of centripetal acceleration changes depending on the position on the Ferris wheel.

The activity will demonstrate how centripetal acceleration always points towards the center.

At the top, the centripetal acceleration is downwards, while at the bottom, it is upwards.

Transcripts

Browse More Related Video

Circular Motion Ferris Wheel Problem

Uniform Circular Motion - 3 - Ferris Wheel

Circular motion and apparent weight

Uniform Circular Motion and Centripetal Force

Circular Motion: Acceleration (Angular, Tangential, Centripetal)

High School Physics - Centripetal Acceleration

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsFerris WheelCentripetal ForceAccelerationVelocityRadiusTurnsCalculationEducationalScience