Circular motion and apparent weight
TLDRIn this educational video, the instructor tackles a physics problem involving the apparent weight of a person on a Ferris wheel with a radius of 11 meters, a 70 kg person, and a 30-second rotation period. The video emphasizes the importance of struggling with problems to learn effectively. It explains that apparent weight changes due to the normal force, which is what we feel, not gravity. The instructor guides through the calculations for apparent weight at the top and bottom of the Ferris wheel, highlighting the difference in acceleration directions and how it affects the normal force. The video concludes with a comparison of the apparent weight at the top and bottom, showing that one feels lighter at the top and heavier at the bottom due to centripetal acceleration.
Takeaways
- 🧭 The problem involves calculating the apparent weight of a person at the top and bottom of a Ferris wheel with a given radius, mass, and rotation period.
- 🤔 The instructor emphasizes that confusion is a natural part of the learning process and encourages students to work through it rather than just watching the solution.
- 📚 The concept of apparent weight is explained as the normal force felt by a person, which is different from gravitational force.
- 🌐 At the top of the Ferris wheel, the apparent weight is less than the gravitational force due to the centripetal acceleration directed towards the center of the circle.
- 📉 The formula used to calculate the apparent weight at the top is n = mg - m(v^2/R), where n is the normal force, m is mass, g is gravitational acceleration, v is velocity, and R is radius.
- ⏱ The velocity (v) of the Ferris wheel is calculated using v = 2πR/T, with R being the radius and T the period of rotation.
- 🔢 The instructor uses Python as a calculator to find the numerical values for the problem, demonstrating a practical approach to solving physics problems.
- 📈 At the bottom of the Ferris wheel, the apparent weight is greater than the gravitational force because the centripetal acceleration is now in the positive y-direction.
- 📘 The formula for the apparent weight at the bottom is n = mg + m(v^2/R), showing the difference in calculation due to the direction of acceleration.
- 💡 The lesson highlights the importance of understanding the direction of forces and acceleration when analyzing circular motion and its effects on apparent weight.
- 🎢 The Ferris wheel example is used to illustrate real-world applications of physics concepts, making the subject more relatable and engaging for students.
Q & A
What is the primary question addressed in the video?
-The primary question addressed is what the apparent weight of a person is at the top and bottom of a Ferris wheel.
What are the given parameters for the Ferris wheel problem?
-The Ferris wheel has a radius of 11 meters, the mass of the person is 70 kilograms, and it takes 30 seconds to complete one revolution.
What forces act on a person at the top of the Ferris wheel?
-At the top of the Ferris wheel, the forces acting on the person are the gravitational force pulling down and the normal force from the seat pushing up.
Why does a person feel lighter at the top of the Ferris wheel?
-A person feels lighter at the top of the Ferris wheel because the normal force is less than the gravitational force, resulting in a lower apparent weight.
What is the direction of acceleration for a person at the top of the Ferris wheel?
-At the top of the Ferris wheel, the direction of acceleration is towards the center of the circle, which is downward.
How is the apparent weight calculated at the top of the Ferris wheel?
-The apparent weight at the top of the Ferris wheel is calculated using the formula 'n = mg - (mv^2 / r)', where 'm' is the mass, 'g' is the acceleration due to gravity, 'v' is the velocity, and 'r' is the radius of the Ferris wheel.
How is the velocity of the Ferris wheel calculated?
-The velocity 'v' is calculated using the formula 'v = (2 * π * r) / T', where 'r' is the radius and 'T' is the time taken for one revolution.
What is the calculated velocity of the Ferris wheel?
-The calculated velocity of the Ferris wheel is approximately 2.3 meters per second.
What is the apparent weight of a person at the top of the Ferris wheel compared to their actual weight?
-The apparent weight of the person at the top of the Ferris wheel is 682.6 N, which is less than their actual weight of 686 N.
What changes in the forces acting on a person at the bottom of the Ferris wheel?
-At the bottom of the Ferris wheel, the direction of acceleration changes to upward, making the normal force greater than the gravitational force.
How is the apparent weight calculated at the bottom of the Ferris wheel?
-The apparent weight at the bottom of the Ferris wheel is calculated using the formula 'n = mg + (mv^2 / r)'.
What is the apparent weight of a person at the bottom of the Ferris wheel?
-The apparent weight of the person at the bottom of the Ferris wheel is 689.4 N, which is greater than their actual weight.
Outlines
🎡 Understanding Apparent Weight on a Ferris Wheel
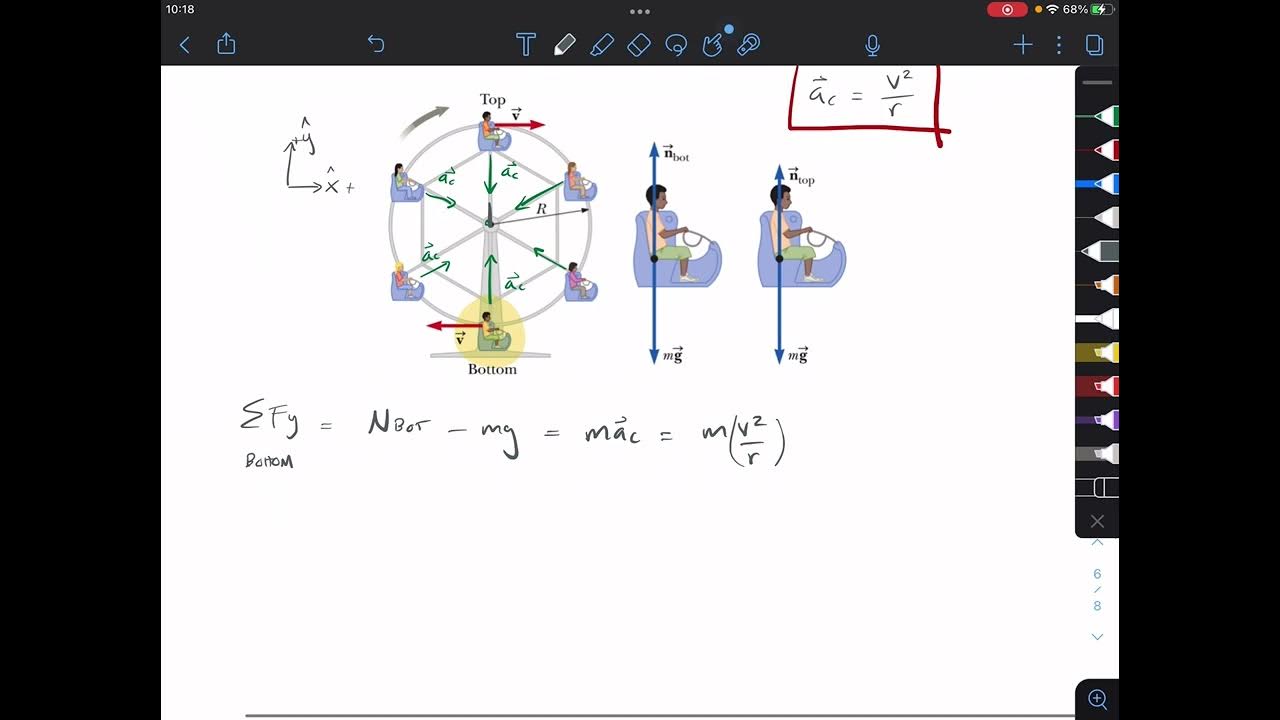
This paragraph introduces a physics problem involving the apparent weight of a person on a Ferris wheel with a radius of 11 meters, a person's mass of 70 kilograms, and a rotation period of 30 seconds. The teacher emphasizes the importance of problem-solving and not getting stuck, encouraging students to work through their confusion. The concept of apparent weight is explained in contrast to gravitational force, highlighting that we feel the normal force, not gravity itself. At the top of the Ferris wheel, the normal force is less than the gravitational force, leading to a sensation of reduced weight, akin to the feeling in a descending elevator. The forces acting on the person are diagrammed, and the equation for net force in the Y direction is set up to solve for the normal force, considering the centripetal acceleration towards the center of the circular motion.
📉 Calculating Apparent Weight at the Top and Bottom of the Ferris Wheel
The second paragraph continues the physics problem by calculating the apparent weight of a person at the top and bottom of the Ferris wheel. The teacher uses Python as a calculator to find the velocity of the Ferris wheel, which is critical for determining the centripetal acceleration. At the top, the normal force is less than the gravitational force due to the downward acceleration, resulting in a sensation of reduced weight. The formula n = mg - m(v^2/R) is used to calculate the normal force, and the velocity is found to be 2.3 m/s, leading to an apparent weight slightly less than the person's actual weight. In contrast, at the bottom, the person experiences an upward acceleration, increasing the normal force and resulting in a sensation of increased weight. The formula n = mg + m(v^2/R) reflects this, with the calculated normal force being greater than the gravitational force, thus the person feels heavier. The teacher wraps up by encouraging students to enjoy the process, even if they initially find it confusing.
Mindmap
Keywords
💡Ferris Wheel
💡Apparent Weight
💡Radius
💡Mass
💡Centrifugal Force
💡Normal Force
💡Gravitational Force
💡Acceleration
💡Velocity
💡Tower of Terror
Highlights
The apparent weight of a person on a Ferris wheel changes depending on their position.
At the top of the Ferris wheel, the normal force is less than the gravitational force, resulting in a lower apparent weight.
The sensation of reduced weight at the top is similar to the feeling in a descending elevator.
The size of the Ferris wheel can affect the intensity of the weight change sensation.
Force diagram illustrates the forces acting on a person at the top of the Ferris wheel.
The net force in the Y direction equals mass times the acceleration in the Y direction.
Acceleration of an object in circular motion is given by the formula v^2/R.
The velocity of the Ferris wheel can be calculated using the formula 2πR/T.
At the top of the Ferris wheel, the normal force is calculated as mg - m(v^2/R).
The apparent weight at the top is slightly less than the actual weight due to the velocity.
The person feels heavier at the bottom of the Ferris wheel due to upward acceleration.
The normal force at the bottom is calculated as mg + m(v^2/R), which is greater than the gravitational force.
The sensation of weight change is realistic and not extreme on a typical Ferris wheel.
The instructor emphasizes the importance of working through problems rather than just watching solutions.
Students are encouraged to pause the video and work on the problem before continuing to watch.
The instructor uses Python as a calculator for solving the problem, showcasing a practical application.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: