DIFFERENTIATION 1: HOW TO USE CALCULATOR TO FIND THE DERIVATIVE OF A LIMIT FUNCTIONS
TLDRIn this educational video, Darling Fee guides viewers on how to use a scientific calculator to solve limit functions. She demonstrates step-by-step calculations for four limit problems, emphasizing the importance of approaching but not reaching the limit value. By entering fractions and close values, viewers learn to evaluate limits as x approaches specific numbers, with examples including approaching one, two, three, and negative one. The video concludes with the correct answers for each problem, encouraging viewers to subscribe for more informative content.
Takeaways
- 📚 The video is an educational tutorial on using a scientific calculator to solve limit problems in mathematics.
- 🔢 The first example demonstrates how to evaluate the limit of (s^3 - 1) / (s - 1) as s approaches 1, illustrating that the limit is 3.
- 🚫 The script emphasizes that the calculator should not be used with the exact value the variable is approaching to avoid errors.
- 📉 It shows how to use the calculator to find the limit by entering values close to, but not equal to, the point of approach.
- 📈 The second problem involves finding the limit of (x^2 - 7x + 10) / (x^2 - 4) as x approaches 2, with the correct answer being -3/4.
- 📝 The third example explains how to calculate the limit of (9 - x^2) / (sqrt(x^2 + 7)) as x approaches 3, resulting in a limit close to 8.
- 📌 The fourth and final problem is about finding the limit of [(x + 3) / (2x - 1)] as x approaches -1, with the limit being 1.5 or 3/2.
- 👍 The presenter encourages viewers to subscribe to the channel for more educational content on various topics.
- 💻 The tutorial provides step-by-step instructions on using the scientific calculator for limit calculations, including entering fractions and brackets.
- 📝 The importance of checking the calculator input is highlighted to ensure accuracy, especially for examination purposes.
- 👋 The video concludes with a reminder to subscribe and a thank you note to the viewers for their time.
Q & A
What is the main topic of the video?
-The main topic of the video is to teach viewers how to use a scientific calculator to solve questions involving limit functions.
What is the first limit function the video demonstrates how to solve?
-The first limit function demonstrated is the limit of (s^3 - 1) / (s - 1) as s approaches 1.
Why is it incorrect to input the value of x as 1 in the first example?
-It is incorrect because the limit is defined as x approaching 1, not equal to 1. Using x = 1 would result in an error on the calculator, as the expression is undefined at that point.
What does the video suggest to do if you want to see the result when x is close to 1?
-The video suggests entering a number very close to 1, such as 0.9999999, to observe the behavior of the function as x approaches 1.
What is the result of the first limit function when x is close to 1?
-When x is close to 1, the result of the first limit function is 3.
What is the second limit function the video discusses?
-The second limit function discussed is the limit of (x^2 - 7x + 10) / (x^2 - 4) as x approaches 2.
How does the video suggest finding the limit as x approaches 2?
-The video suggests entering a number close to 2, such as 1.9999999, and observing the result on the calculator.
What is the result of the second limit function when x is close to 2?
-When x is close to 2, the result of the second limit function is -3/4.
What is the third limit function the video covers?
-The third limit function covered is the limit of (9 - x^2) / (sqrt(x^2 + 7)) as x approaches 3.
How does the video suggest finding the limit as x approaches 3?
-The video suggests using a number very close to 3, such as 2.9999999, and observing the result on the calculator.
What is the result of the third limit function when x is close to 3?
-When x is close to 3, the result of the third limit function is approximately 7.999.
What is the final limit function the video presents?
-The final limit function presented is the limit of [(x + 3) / (x^2 + 3x - 2)] as x approaches -1.
How does the video suggest finding the limit as x approaches -1?
-The video suggests using a number very close to -1, such as -1.0001, and observing the result on the calculator.
What is the result of the final limit function when x is close to -1?
-When x is close to -1, the result of the final limit function is 1.5, which is equivalent to 3/2.
Outlines
📚 Introduction to Using a Scientific Calculator for Limits
The video begins with the host, Darling Fee, welcoming viewers to the channel and encouraging them to subscribe for updates on various topics. The main focus of this segment is to demonstrate how to use a scientific calculator to solve limit functions. The first example involves calculating the limit of (s^3 - 1) / (s - 1) as s approaches 1. The host explains the process of entering the fraction into the calculator, pressing 'calc', and then inputting a value close to 1 to find the limit, which turns out to be 3. The importance of not using the value 1 itself is emphasized, as it would result in an error. The process is repeated with values from both sides of 1 to confirm the limit.
🔍 Evaluating Limits with a Scientific Calculator
This paragraph continues the tutorial on using a scientific calculator to evaluate limits. The host walks through solving three more limit problems. The second problem involves finding the limit of (x^2 - 7x + 10) / (x^2 - 4) as x approaches 2, resulting in the answer -3/4. The third problem is about the limit of (9 - x^2) / (sqrt(x^2 + 7)) as x approaches 3, yielding an approximate answer of 8. The final problem in this segment is calculating the limit of [(x + 3) / (x - 1)] as x approaches -1, which gives an answer close to 1.5 or 3/2. The host stresses the importance of entering expressions correctly and checking calculations for accuracy, especially in an examination context. The segment concludes with a reminder to subscribe and thanks for watching.
Mindmap
Keywords
💡Scientific Calculator
💡Limit
💡Fraction
💡Approaching
💡Error
💡Calc Button
💡Expression
💡Root
💡Bracket
💡Subscription
Highlights
Introduction to the channel and a request to subscribe.
Overview of the day's topic: solving limit functions using a scientific calculator.
Demonstration of entering a fraction expression on the calculator.
Explanation of why entering the exact limit value can result in an error.
Technique of using values close to the limit point to avoid errors.
First example problem: Evaluating the limit of (x^3 - 1) / (x - 1) as x approaches 1.
Process of solving the first problem by using values close to 1 from the left and right.
Solution of the first problem: The limit is 3.
Second example problem: Evaluating the limit of (x^2 - 7x + 10) / (x^2 - 4) as x approaches 2.
Demonstration of entering the second expression on the calculator.
Solution of the second problem: The limit is -3/4.
Third example problem: Evaluating the limit of (9 - x^2) / (x - sqrt(x^2 + 7)) as x approaches 3.
Process of solving the third problem using values close to 3 from both sides.
Solution of the third problem: The limit is approximately 8.
Final example problem: Evaluating the limit of (x + 3) / (2x - 1) as x approaches -1.
Explanation of entering the final expression on the calculator.
Solution of the final problem: The limit is 1.5.
Summary and conclusion of the presentation, with a reminder to subscribe.
Transcripts
Browse More Related Video
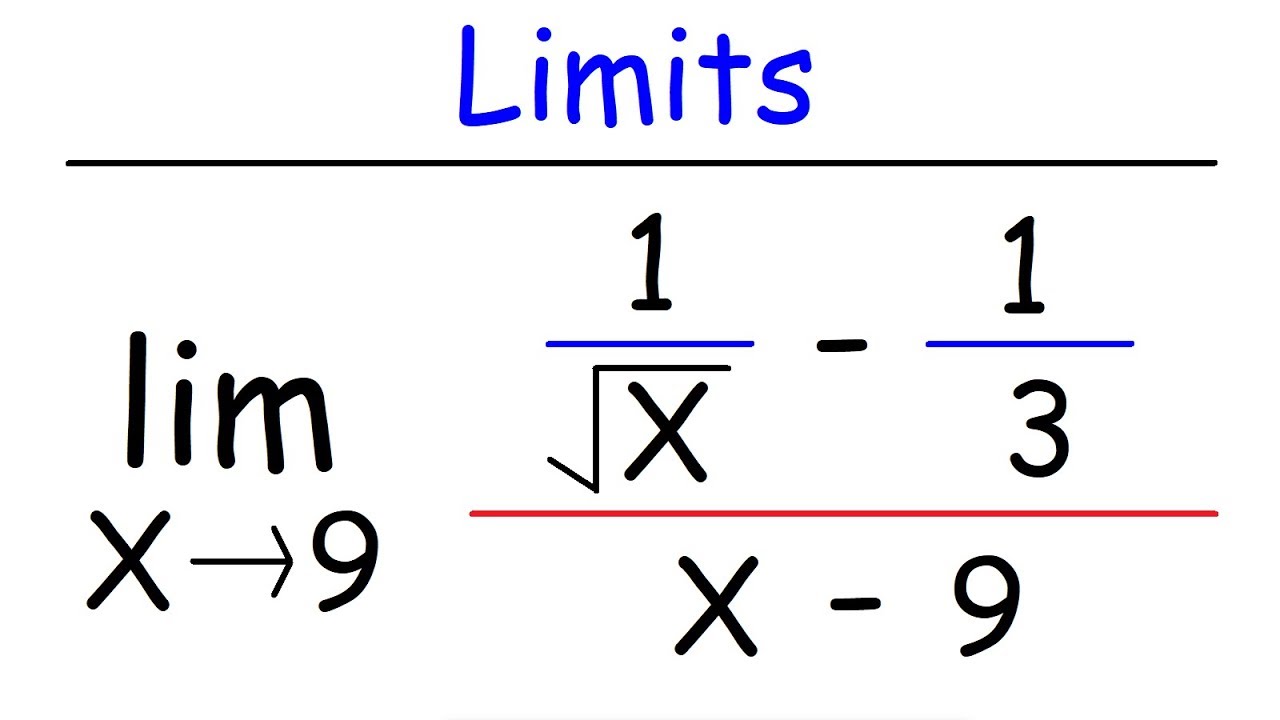
Limits

One-sided limits from tables | Limits and continuity | AP Calculus AB | Khan Academy

INTEGRATION PART 1: SIMPLE CALCULATOR TECHNIQUES FOR SOLVING INDEFINITE INTEGRAL- WASSCE MATHS

INTEGRATION PART 2: CALCULATOR TECHNIQUES ON INDEFINITE INTEGRATION OF TRIGONOMETRIC FUNCTIONS

Introduction to Limits (NancyPi)
DIFFERENTIATION PART 2: USING CALCULATOR TO FIND THE DERIVATIVES OF POLYNOMIALS
5.0 / 5 (0 votes)
Thanks for rating: