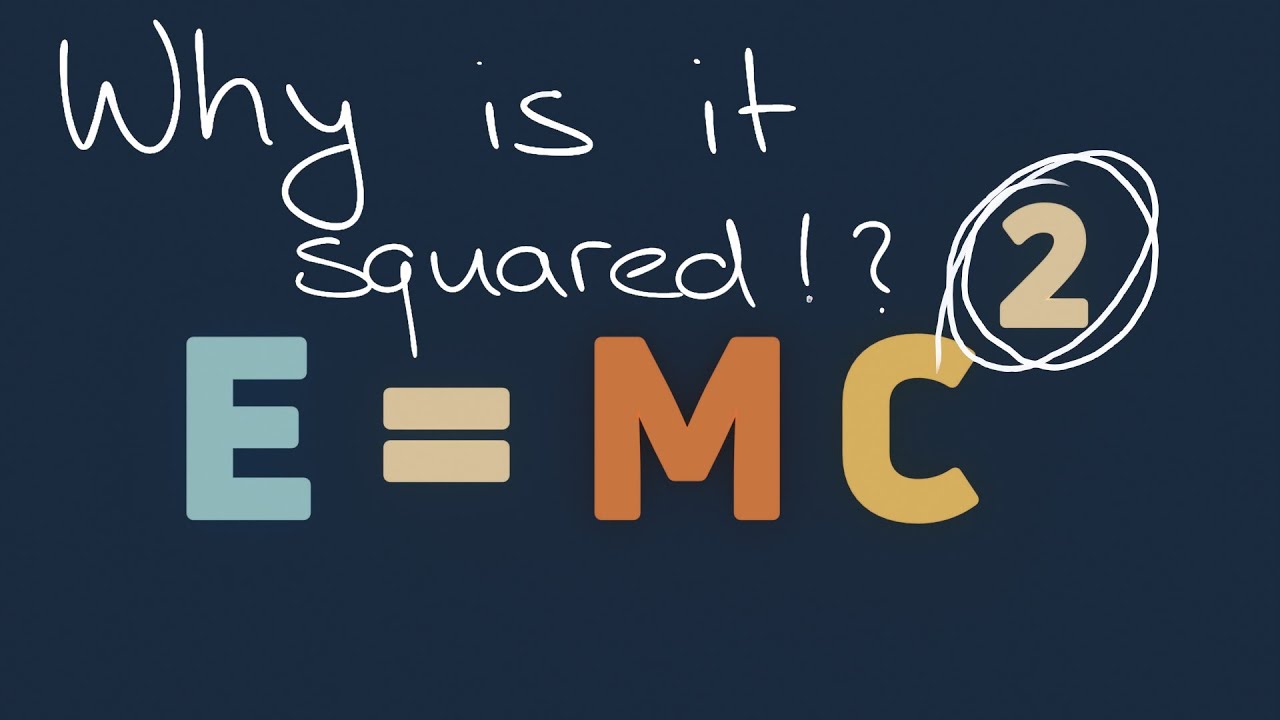E=mc2
TLDRIn this AP Physics essentials video, Mr. Andersen explains the renowned equation E=mc^2, developed by Albert Einstein in 1905, which illustrates the equivalence of energy and mass. He clarifies that mass can be converted into energy and vice versa, and the equation quantifies the energy released during this conversion. Andersen discusses the conservation of mass-energy, emphasizing that mass and energy are interchangeable. He provides examples, such as carbon-12 and particle accelerators, to demonstrate mass-energy conversion. The video concludes with a practical application, calculating the immense energy potential in 5 kilograms of uranium 235, highlighting the profound implications of Einstein's equation.
Takeaways
- 🌟 E=mc² is arguably the most famous equation in physics, formulated by Albert Einstein in 1905, representing the equivalence of energy and mass.
- 🔍 The equation demonstrates that energy can be converted into mass and vice versa, and it quantifies the amount of energy released in this conversion process.
- 🚫 Traditional conservation laws, such as mass and energy conservation, have been adjusted to the unified conservation of mass-energy, acknowledging the convertibility of mass and energy.
- 🌌 The speed of light (c) plays a crucial role in the equation, with energy (E) being equal to mass (m) times the speed of light squared (c²), indicating the vast amount of energy contained in a small amount of matter.
- 💥 Einstein's realization of energy-mass equivalence led to significant developments such as atomic bombs and nuclear energy.
- 🔬 The script provides an example of how the atomic mass unit is defined based on 1/12 the mass of carbon-12, illustrating the concept of mass-energy equivalence.
- 🔍 When the constituents of an atom (protons, neutrons, and electrons) are separated, their combined mass is less than the mass of the whole atom, indicating the mass deficit is due to the binding energy within the atom.
- ⚛️ Particle accelerators, like the Large Hadron Collider, demonstrate the conversion of energy into mass, as protons gain mass as they approach the speed of light.
- 🚀 The speed of light acts as a universal speed limit; as particles accelerate, their mass increases, requiring more energy, and they can never reach the speed of light.
- 📐 The equation E=mc² can be used to calculate the energy contained within a given mass, as illustrated with the example of uranium-235, highlighting the immense energy potential in matter.
- 💡 The script concludes by reinforcing the understanding of why the conservation of mass was replaced by the conservation of mass-energy, due to the mutual convertibility of mass and energy.
Q & A
What is the most famous equation in physics?
-The most famous equation in physics is E=mc^2, which was developed by Albert Einstein in 1905.
What does the equation E=mc^2 represent?
-E=mc^2 represents energy-mass equivalence, showing that energy can be converted into mass and mass can be converted back into energy.
What are the two conservation rules mentioned in the script?
-The two conservation rules mentioned are the conservation of mass and the conservation of energy.
How is the conservation of mass demonstrated in the script?
-The conservation of mass is demonstrated by showing that if a piece of wood is chopped in half, the mass of the two pieces is equal to the mass of the original piece of wood.
What is the modern understanding of mass and energy in terms of conservation?
-The modern understanding is the conservation of mass-energy, which states that mass and energy are essentially the same thing and can be converted into each other.
What is the speed of light squared in the context of E=mc^2?
-In the context of E=mc^2, the speed of light squared (c^2) is a very large number, indicating that a small amount of matter contains a huge amount of energy.
How does the script explain the conversion of mass into energy in atomic particles?
-The script explains that when atomic particles are deconstructed, the mass of the individual parts is greater than the mass of the whole, indicating that the mass difference is converted into energy that holds the atom together.
What is an example of mass to energy conversion mentioned in the script?
-An example mentioned is the Large Hadron Collider, where protons are accelerated to near the speed of light, causing them to gain mass due to the conversion of energy into mass.
Why can't an object reach the speed of light according to the script?
-An object cannot reach the speed of light because as it approaches the speed of light, its mass increases, requiring more energy to accelerate it, which would eventually require infinite energy.
How can the equation E=mc^2 be used to calculate the energy contained in a certain amount of matter?
-The equation E=mc^2 can be used to calculate the energy in matter by multiplying the mass of the matter by the speed of light squared.
What is an example given in the script to illustrate the vast amount of energy contained in a small amount of matter?
-The script gives the example of 5 kilograms of uranium 235, which, when calculated using E=mc^2, shows that it contains enough energy to light a light bulb for millions of years.
Outlines
🔬 E=mc²: The Fundamental Equation of Mass-Energy Equivalence
In this segment, Mr. Andersen introduces the renowned equation E=mc², developed by Albert Einstein in 1905, which encapsulates the concept of energy-mass equivalence. He explains that energy can be converted into mass and vice versa, and this equation quantifies the amount of energy released during such a conversion. The video discusses the conservation laws of mass and energy, highlighting how the discovery of mass-energy conversion has led to the understanding of mass-energy conservation. Mr. Andersen uses the example of carbon-12 to illustrate how mass can be converted into energy, demonstrating the binding energy that holds an atom together. He also touches on the implications of E=mc² for atomic bombs and nuclear energy, showcasing the immense energy potential contained within matter.
💡 Harnessing Energy from Mass: The Power of Nuclear Reactions
This paragraph delves into the practical applications of the mass-energy equivalence principle, focusing on the energy potential locked within matter. Mr. Andersen provides an example of uranium-235 to demonstrate the vast amount of energy that can be derived from a relatively small amount of mass. He calculates the energy content of 5 kilograms of uranium using the E=mc² equation, revealing a staggering quantity of energy that could power a light bulb for millions of years. The summary also addresses the inefficiencies and energy losses in real-world applications but emphasizes the enormous energy reserves inherent in nuclear materials. The paragraph concludes with a reflection on the significance of the mass-energy conservation theory, which has replaced the traditional conservation of mass due to the convertible nature of mass and energy.
Mindmap
Keywords
💡E=mc2
💡Energy-Mass Equivalence
💡Conservation Laws
💡Mass
💡Speed of Light
💡Atomic Mass Unit
💡Binding Energy
💡Particle Accelerator
💡Nuclear Energy
💡Uranium-235
Highlights
E=mc2 is the most famous equation in physics, developed by Albert Einstein in 1905.
The equation represents energy-mass equivalence, showing that energy can be converted into mass and vice versa.
E=mc2 quantifies the amount of energy released during the conversion of mass to energy.
Conservation of mass states that mass cannot be created or destroyed, as illustrated by chopping wood.
Conservation of energy implies that energy cannot be created or destroyed, as seen in the energy transfer from the sun to a tree.
20th-century discoveries showed that mass can be converted into energy and energy into mass, leading to the conservation of mass-energy.
Mass and energy are essentially the same, which can be converted using the E=mc2 equation.
The speed of light squared is a very large number, indicating a significant amount of energy in a small amount of matter.
Einstein's realization of energy locked in matter led to developments like atomic bombs and nuclear energy.
Carbon-12 is used as the basis for defining the atomic mass unit, with a mass of 12.000 atomic mass units.
Deconstructing carbon-12 into its constituent parts reveals more mass when separated than when intact, due to binding energy.
Binding energy is the energy that holds an atom together, converting mass into energy.
Particle accelerators, like the Large Hadron Collider, demonstrate the conversion of energy into mass as protons accelerate.
Approaching the speed of light, protons gain mass, illustrating the energy-mass conversion.
The speed of light is a universal speed limit, as infinite energy would be required to reach it.
Calculating the energy in 5 kilograms of uranium 235 using E=mc2 results in a massive amount of energy.
The energy contained in uranium could light a light bulb for millions of years, showcasing the vast energy potential in matter.
The theory of conservation of mass was replaced by the theory of conservation of mass-energy due to the convertible nature of mass and energy.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: