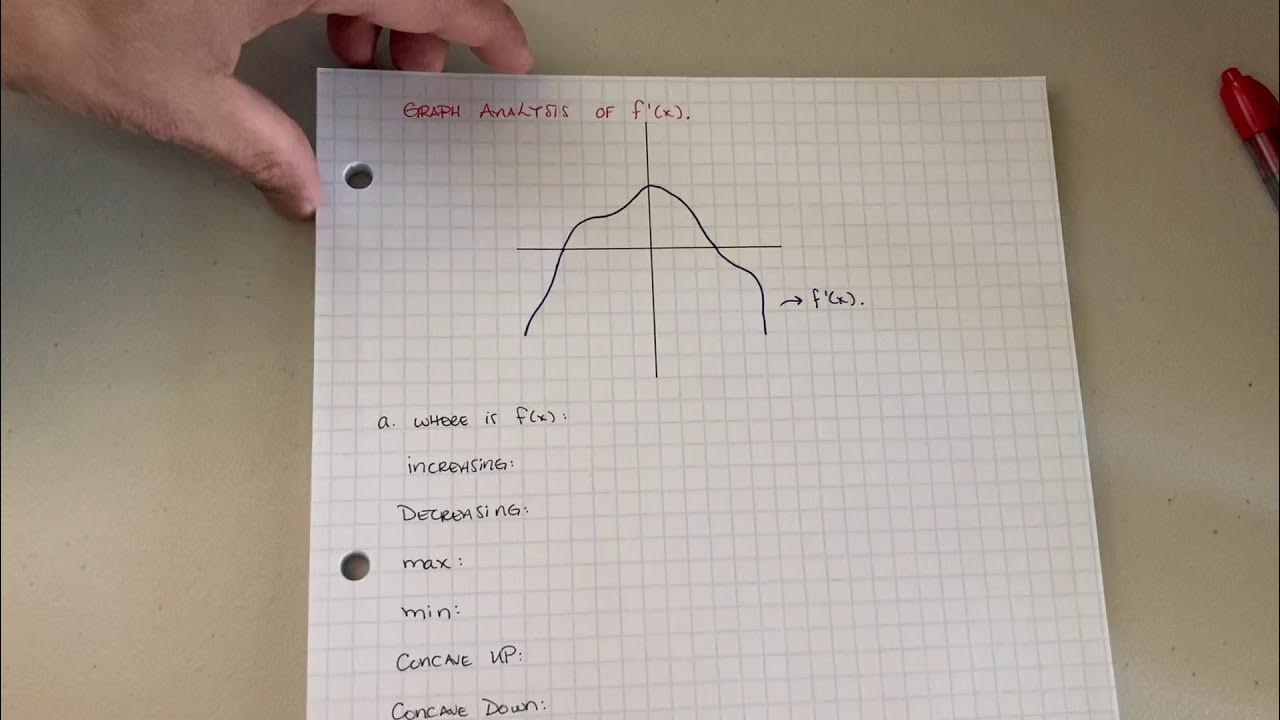
Where is the function increasing, decreasing, concave up, concave down, and points of inflection?
TLDRThis calculus tutorial focuses on understanding the concepts of increasing, decreasing, concave up, and concave down functions, as well as identifying points of inflection. The instructor emphasizes the importance of recognizing these characteristics from a graph without needing to perform algebra. The tutorial walks through two examples, explaining how to determine intervals for increasing and decreasing functions and how to identify concave sections and points of inflection. It also clarifies the difference between the function being increasing and the first derivative being positive, and provides clear instructions on how to notate intervals and points.
Takeaways
- 📈 To determine where a function is increasing, look for where the curve is rising; this corresponds to intervals where the first derivative is positive.
- 📉 For a function to be decreasing, identify where the curve is falling; this is represented by intervals with a negative first derivative.
- 😊 Remember that a 'U' shape (like a happy face) indicates the function is concave up, which means the second derivative is positive in that region.
- 😞 A downward-facing parabola signifies the function is concave down, indicating a negative second derivative in that region.
- ⚠️ Be cautious with intervals that include points where the function is flat (horizontal tangents); these are still considered increasing if the overall trend is upwards.
- 📐 When identifying points of inflection, look for where the function changes concavity, which requires the second derivative to change sign.
- 🔢 For points of inflection, provide both the x and y coordinates, as these points mark significant changes in the function's curvature.
- 🤔 Be aware of the difference between a function that is increasing (first derivative > 0) and a function that has a positive first derivative; the latter does not include horizontal tangents.
- 📊 When graphing, use open intervals (parentheses) to denote the range where the function is increasing or decreasing, excluding the endpoints.
- 🔁 Use a union (∪) to combine multiple intervals into a single representation, especially when there are more than one.
- ❌ At points where the second derivative does not exist (like sharp turns), exclude these from the concavity analysis.
- 📋 Always label points of inflection clearly with their coordinates to distinguish them from intervals.
Q & A
What is the main focus of the calculus tutorial discussed in the transcript?
-The main focus of the calculus tutorial is to understand the concepts of where a function is increasing, decreasing, concave up, concave down, and identifying points of inflection without needing to perform any algebra.
How does the tutorial define the intervals where the function is increasing?
-The tutorial defines the intervals where the function is increasing by observing where the curve on the graph is going up. It specifies the intervals as open, meaning not including the endpoints, using parentheses like (1,3).
What is the notation used for intervals where the function is decreasing?
-The notation used for intervals where the function is decreasing is similar to increasing intervals but uses a union to combine multiple intervals, like 0 to 1 Union 3 to 4.
How is concavity identified in the tutorial?
-Concavity is identified by looking at the shape of the graph and comparing it to the shape of a 'happy face' parabola for concave up and the inverse for concave down.
What does the tutorial say about the function's concavity at the point where the second derivative does not exist?
-The tutorial states that at points where the second derivative does not exist, such as at x=4, you should not consider the function as concave up or down and should exclude these points from the analysis.
How are points of inflection identified and represented in the tutorial?
-Points of inflection are identified where the function changes concavity, from concave up to down or vice versa. They are represented by their coordinates, such as (2,3), and are clearly labeled as points with an 'x, y' format.
What is the difference between considering a function as increasing and where the first derivative is greater than zero?
-A function is considered increasing if it goes up overall, even if there are horizontal tangent points. However, if the question asks for where the first derivative is greater than zero, horizontal tangent points are not included, and the intervals are specified without them.
How does the tutorial handle horizontal tangent points when determining intervals of increase?
-The tutorial includes horizontal tangent points in the intervals of increase because the function continues to go up overall, even if there is a flat section.
What is the notation used for intervals where the function is concave up?
-The notation for intervals where the function is concave up is similar to that for increasing intervals, using parentheses and union where necessary, like 2 to 4 Union 5 to 7.
How many points of inflection are there in the second example provided in the tutorial?
-In the second example, there are three points of inflection, which are represented by their coordinates: (2,2), (4,3), and (5,4).
What is the significance of the 'happy face' parabola reference in the tutorial?
-The 'happy face' parabola reference is a mnemonic device to help visualize and identify concave up sections of a function's graph, as the upward curve of a happy face resembles the shape of a concave up parabola.
Outlines
📚 Calculus Tutorial: Analyzing Function Behavior
This paragraph provides a comprehensive guide for understanding the behavior of a function in a Calculus one class. The tutorial begins by explaining how to determine where a function is increasing or decreasing by observing the graph. It emphasizes the importance of recognizing open intervals and uses union notation for clarity. The speaker then moves on to identifying concave up and concave down sections of the function, using visual cues like the shape of a 'happy face' parabola. Special attention is given to points of inflection, where the function changes concavity, and the need to provide both x and y coordinates for these points. The tutorial concludes with a reminder to label points clearly to avoid confusion.
🔍 Advanced Function Analysis: Increasing, Decreasing, and Concavity
In this paragraph, the tutorial delves deeper into the analysis of a function's behavior, focusing on the nuances of identifying intervals where the function is increasing or decreasing. It highlights a tricky aspect where even a flat section of the function can still be considered increasing if it continues to rise. The explanation then proceeds to describe how to identify concave up and concave down sections, providing clear examples and emphasizing the importance of recognizing changes in concavity. The paragraph concludes with the identification of points of inflection, which are critical transition points in the function's curvature. The tutorial stresses the need to accurately provide the coordinates for these points, distinguishing them from intervals with a clear notation.
Mindmap
Keywords
💡Calculus
💡Increasing Function
💡Decreasing Function
💡Concave Up
💡Concave Down
💡Inflection Point
💡Open Interval
💡Union
💡First Derivative
💡Second Derivative
💡Horizontal Tangent
Highlights
The importance of understanding the concepts of calculus for Calculus one class is emphasized.
No algebra is required; it's purely about grasping the concepts.
The tutorial begins with identifying where the original function f is increasing by observing the graph's upward trend.
Interval notation is used to denote the sections of the function that are increasing, excluding endpoints.
The function is found to be increasing in the intervals (1,3) and (4,6).
For decreasing sections, the function goes from 0 to 1 and from 3 to 4.
The concept of concavity is introduced with the analogy of a 'happy face' parabola for concave up sections.
The function is concave up from 1 to 2 on the graph.
Points of inflection are identified where the concavity changes, such as from concave up to concave down at (2,3).
The tutorial moves on to a second function, noting the tricky aspect of including horizontal tangent points as increasing.
The function is increasing in the intervals (0,1) union (3,7) despite a horizontal tangent at 5.
For the decreasing function, the intervals are identified as (1,2), (3,4), and (5,7).
Concave up sections for the second function are from 2 to 4 and from 5 to 7.
Concave down sections are from 0 to 2 and from 4 to 5.
Three points of inflection are identified at (2,2), (4,3), and (5,4) for the second function.
The distinction between intervals and points is clarified, with intervals denoted by unions and points by commas.
The tutorial concludes with a reminder to practice and understand the concepts thoroughly before moving on.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: