GRAPHS OF SINE AND COSINE FUNCTIONS || PRE-CALCULUS

WOW MATH

4 Jan 202235:01

EducationalLearning

32 Likes 10 Comments

TLDRThis video lesson delves into the graphs of sine and cosine functions, essential for understanding circular functions. The instructor provides a detailed table of values for the sine function and explains its properties, such as domain, range, and periodicity. The amplitude and continuous nature of these functions are highlighted. The lesson continues with the cosine function, emphasizing its similarities and differences with sine. Transformations like vertical shifts and scaling are discussed, along with the impact on amplitude and period. The tutorial concludes with practical examples of graphing sine and cosine functions with various transformations, aiming to enhance viewers' comprehension of these fundamental mathematical concepts.

Takeaways

📚 The video lesson covers the graphs of sine and cosine functions, building on previous knowledge of circular functions.
📈 The sine function, represented as y = sin(θ), has specific values at key angles such as 0, π/6, π/4, π/3, π/2, 2π/3, 3π/4, and π, with values ranging from -1 to 1.
📉 The cosine function, y = cos(θ), also has a range from -1 to 1 and shares the same domain as the sine function, all real numbers.
🔁 Both sine and cosine functions are periodic with a period of 2π, meaning their patterns repeat every 2π units along the x-axis.
📊 The amplitude of the sine and cosine functions is 1, representing the maximum value they can reach from the midline.
📐 The sine function is continuous, meaning it has no breaks or gaps in its graph.
🔢 The maximum and minimum values of the sine function are 1 and -1, respectively, indicating the peak and trough of the wave.
🌐 The properties of sine and cosine functions can be modified by transformations such as vertical shifts (up and down) and horizontal shifts (left and right).
🔍 The amplitude of a transformed sine or cosine function can be calculated using the absolute value of the coefficient in front of the sine or cosine term.
📝 Examples are given to illustrate how to find the period, amplitude, and shifts for different variations of sine and cosine functions, such as y = a * sin(b * θ) + d.
👋 The video concludes with an invitation to like, subscribe, and hit the bell for more educational content on the channel.

Q & A

What are the key properties of the sine function discussed in the video?
-The sine function has the following key properties: domain of all real numbers, range from -1 to 1, maximum value of 1, minimum value of -1, and it is a continuous and periodic function with a period of 2π.
What is the range of the sine function?
-The range of the sine function is from -1 to 1, which means the output values of y (sine of an angle) will always be between -1 and 1, inclusive.
What is the amplitude of the basic sine function?
-The amplitude of the basic sine function is 1, which represents the maximum value or the 'height' of the sine wave from the midline.
How can you find the amplitude of a sine function given by f(x) = a * sin(b * theta) + c?
-The amplitude of the function f(x) = a * sin(b * theta) + c is the absolute value of 'a', which determines the peak value of the sine wave.
What is the period of the sine function y = sin(theta)?
-The period of the sine function y = sin(theta) is 2π, which means the function repeats its values every 2π units along the x-axis.
How does the cosine function compare to the sine function in terms of domain and range?
-Like the sine function, the cosine function also has a domain of all real numbers and a range from -1 to 1.
What is the relationship between the sine and cosine functions in terms of their maximum and minimum values?
-Both the sine and cosine functions have maximum values of 1 and minimum values of -1, just like the sine function.
How can you determine the period of a transformed sine function, such as y = sin(2x)?
-The period of a transformed sine function y = sin(2x) can be determined using the formula (2π) / |b|, where b is the coefficient of x inside the sine function. For y = sin(2x), the period is π.
What is the effect of a vertical shift on the graph of a sine or cosine function?
-A vertical shift affects the graph of a sine or cosine function by moving the entire graph up or down along the y-axis by a certain amount, determined by the value of 'c' in the function f(x) = a * sin(b * theta) + c or f(x) = a * cos(b * theta) + c.
How does a horizontal shift affect the graph of a sine or cosine function?
-A horizontal shift moves the graph of a sine or cosine function left or right along the x-axis by a certain amount, determined by the value of 'd' in the function f(x) = a * sin(b * (theta - c)) or f(x) = a * cos(b * (theta - c)).
What does the video suggest for understanding the properties of sine and cosine functions?
-The video suggests that understanding the properties of sine and cosine functions can be enhanced by examining their graphs, noting their domain, range, amplitude, and period, and by analyzing how transformations such as shifts and scaling affect their graphs.

Outlines

00:00

📈 Introduction to Sine and Cosine Functions

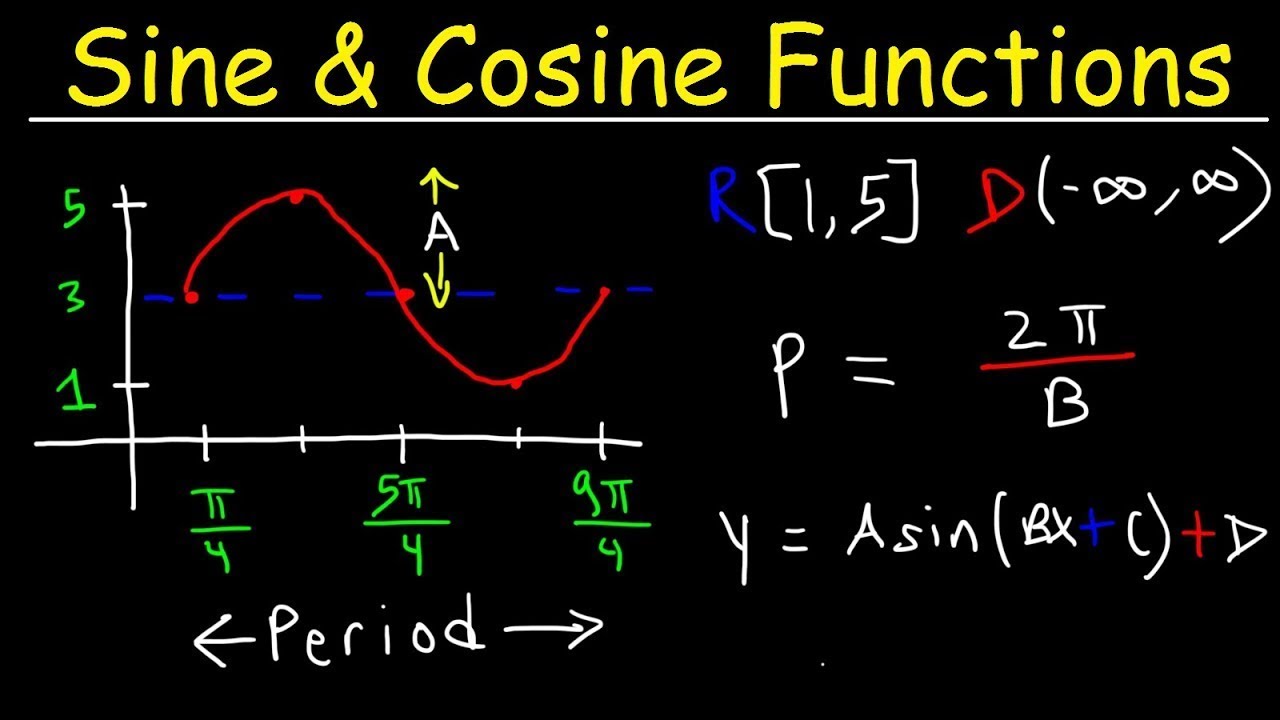
This paragraph introduces the topic of the video, which is the discussion of sine and cosine functions. It mentions previous lessons on circular functions and provides a table of values for the sine function at various angles. The key points include the values of sine at angles like 0, π/6, π/4, π/3, π/2, 2π/3, 3π/4, 5π/6, π, 7π/6, 5π/4, 4π/3, 3π/2, 5π/3, and 7π/4. The paragraph also discusses the graph of the sine function.

05:00

📉 Properties of the Sine Function

This paragraph delves into the properties of the sine function. It states that the domain of the sine function is all real numbers, and the range is from -1 to 1. The maximum value is 1 and the minimum value is -1. The sine function is continuous and periodic with a period of 2π. The amplitude of the sine function is 1, which is the maximum value. The paragraph also discusses the graph of the sine function in detail.

10:01

📈 Properties of the Cosine Function

This paragraph discusses the properties of the cosine function. The domain is the same as the sine function, all real numbers, and the range is also from -1 to 1. The maximum value is 1 and the minimum value is -1. The cosine function is also continuous. The paragraph mentions the graph of the cosine function and compares it to the sine function.

15:25

📊 Transformations of Sine and Cosine Functions

This paragraph explores transformations of sine and cosine functions. It discusses how to find the amplitude and period of functions like y = A sin(Bx) and y = A cos(Bx). The amplitude is the absolute value of A, and the period is given by the formula (2π)/B. The paragraph also covers vertical shifts of the functions using the formula y = A sin(Bx) + C.

20:27

📈 Graphing Sine and Cosine Functions

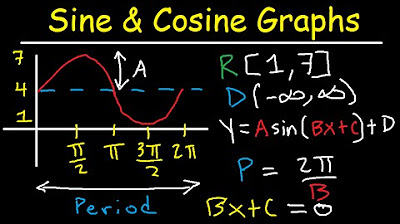
This paragraph focuses on graphing sine and cosine functions. It provides examples of how to graph functions like y = 2 + cos(x) and y = 3 + cos(x) on the same Cartesian coordinate plane. The period, maximum, and minimum values of these functions are discussed. The paragraph also covers how to find the period of functions like y = sin(Bx) using the formula (2π)/B.

25:41

📊 Horizontal and Vertical Shifts

This paragraph discusses horizontal and vertical shifts of sine and cosine functions. It explains how to shift the functions using formulas like y = A sin(B(x - C)) + D and y = A cos(B(x - C)) + D. The amplitude, period, and shifts of the functions are analyzed. Examples are provided to illustrate the concepts.

30:48

📈 Summary of Sine and Cosine Functions

In this concluding paragraph, the video summarizes the key properties and concepts related to sine and cosine functions. It emphasizes the importance of understanding the amplitude, period, shifts, and transformations of these functions. The video encourages viewers to practice graphing and analyzing sine and cosine functions to solidify their understanding. The presenter thanks the viewers for watching and invites them to like, subscribe, and hit the bell for more video tutorials.

Mindmap

Keywords

💡sine function

The sine function is a fundamental mathematical function that relates an angle to the ratio of the length of the opposite side to the hypotenuse in a right-angled triangle. In the context of the video, it is a periodic function used in trigonometry to model periodic phenomena. The script discusses the values of the sine function at various angles, such as sine(0) = 0, sine(pi/6) = 1/2, and sine(pi/2) = 1, illustrating the function's behavior on the unit circle.

💡cosine function

The cosine function is another basic trigonometric function that, like the sine function, describes the ratio of the adjacent side to the hypotenuse in a right-angled triangle. The video script explains the cosine function's values at specific angles, similar to the sine function, and discusses its properties, such as being a continuous and periodic function with a range from -1 to 1.

💡domain

In mathematics, the domain of a function refers to the set of all possible input values (independent variable values) for which the function is defined. The script mentions that the domain of both the sine and cosine functions is all real numbers, indicating that these functions can accept any real number as an input.

💡range

The range of a function is the set of all possible output values (dependent variable values). For the sine and cosine functions discussed in the video, the range is from -1 to 1, meaning that the output of these functions will always be between -1 and 1, inclusive.

💡periodic function

A periodic function is one that repeats its values at regular intervals or periods. The sine and cosine functions are classic examples of periodic functions, each having a period of 2π. This means that after every 2π interval, the function's values repeat, as illustrated by the script's discussion of the function's behavior over a full cycle from 0 to 2π.

💡amplitude

The amplitude of a periodic function is the distance from the function's maximum value to its minimum value, or equivalently, half the vertical distance from the highest to the lowest point of the function's graph. In the video, the amplitude of the basic sine and cosine functions is given as 1, indicating that they oscillate between -1 and 1.

💡continuous function

A continuous function is one where there are no abrupt changes in value, meaning it does not have any 'jumps' or 'breaks' in its graph. The sine and cosine functions are described as continuous in the script, which is a key property that allows for the smooth, unbroken curve seen in their graphs.

💡graph

In the context of the video, a graph refers to the visual representation of the sine and cosine functions, where the x-axis typically represents the angle in radians, and the y-axis represents the function's value. The script describes the process of graphing these functions and discusses the shape and characteristics of their graphs, such as their periodic nature and amplitude.

💡transformation

Transformation in the context of functions refers to the process of modifying the function's graph in various ways, such as shifting, stretching, or reflecting. The script discusses transformations of the sine and cosine functions, such as vertical shifts (e.g., y = 2 + cosine(theta)) and horizontal shifts (e.g., y = cosine(theta - pi/2)), which alter the position and shape of the graph.

💡maximum value

The maximum value of a function is the highest value that the function attains within its domain. For the sine and cosine functions, the script states that the maximum value is 1, indicating that these functions reach their peak at this value before beginning to decrease.

💡minimum value

The minimum value of a function is the lowest value it attains within its domain. For the sine and cosine functions, the script specifies that the minimum value is -1, showing that these functions reach their lowest point at this value before beginning to increase.

Highlights

Introduction to the graphs of sine and cosine functions.

Explanation of the sine function with examples of its values at specific angles.

Graphing of the sine function and its properties such as domain, range, and amplitude.

Discussion on the periodic nature of the sine function with a period of 2π.

Properties of the cosine function, including its domain, range, and continuity.

Graphing the cosine function and its comparison to the sine function.

Transformations of the sine and cosine functions, such as vertical shifts and amplitude adjustments.

Calculation of the amplitude of sine and cosine functions given different coefficients.

Sketching the graph of y = cosine(theta) and y = 2 + cosine(theta) on the same coordinate plane.

Explanation of the period, maximum, and minimum values of transformed cosine functions.

Formula for determining the period of sine and cosine functions with transformations.

Illustration of horizontal and vertical shifts in the context of sine and cosine functions.

Application of transformations to the cosine function with examples.

Detailed explanation of how to graph sine and cosine functions with phase shifts and vertical shifts.

Summary of the properties and graphical representations of sine and cosine functions.

Encouragement to like, subscribe, and hit the bell button for more video tutorials.

Transcripts

Browse More Related Video

Trigonometry - Graphing transformations of sin and cos

Graphing Trigonometric Functions, Phase Shift, Period, Transformations, Tangent, Cosecant, Cosine

How To Graph Trigonometric Functions | Trigonometry

The Graphs of Sine and Cosine (Precalculus - Trigonometry 11)

Graphing Sine and Cosine Trig Functions With Transformations, Phase Shifts, Period - Domain & Range

How to Graph Cosecant and Secant (Precalculus - Trigonometry 15)

Related Tags

Trigonometry Sine Function Cosine Function Graphs Educational Math Tutorial Circular Functions Amplitude Periodicity Domain Range