CIRCLES || PRE-CALCULUS
TLDRThis video lesson delves into the topic of circles, starting with an overview of conic sections and their formation by the intersection of a plane and a cone. The instructor explains the definition of a circle as a set of points equidistant from a center point, known as the center, and introduces the constant distance, the radius. The core focus is on finding the equation of a circle using the standard form, with various examples provided to illustrate the process. The examples demonstrate how to derive the equation of a circle given the center's coordinates and the radius, with the standard form being (x-h)^2 + (y-k)^2 = r^2. The video concludes with a call to action, encouraging viewers to like, subscribe, and stay tuned for more educational content.
Takeaways
- 📚 The video lesson is about circles, focusing on conic sections and their properties.
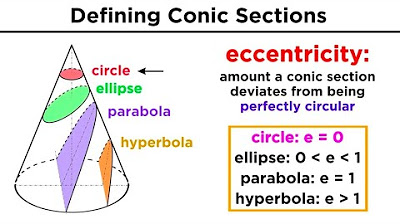
- 📐 A conic section is formed by the intersection of a plane and a cone, resulting in four different types.
- ⭕ A circle is defined as the set of all points on a plane equidistant from a fixed point, known as the center.
- 📏 The distance from the center of a circle to any point on the circle is constant and is called the radius.
- 🔢 The standard form of a circle's equation is \( (x - h)^2 + (y - k)^2 = r^2 \), where \( (h, k) \) is the center and \( r \) is the radius.
- 📈 The video provides examples of how to find the equation of a circle given its center and radius.
- 🌐 An example given is a circle with its center at the origin (0,0) and a radius of 5 units, with the equation \( x^2 + y^2 = 25 \).
- 📍 Another example includes a circle centered at (0,3) with a radius of 6 units, resulting in the equation \( x^2 + (y - 3)^2 = 36 \).
- 🔢 The video explains how to adjust the equation for circles with different centers and radii, such as one centered at (2, -5) with a radius of 10.
- 📘 The process involves substituting the center coordinates \( (h, k) \) and radius \( r \) into the standard equation to derive the specific circle equation.
- 👍 The video encourages viewers to like, subscribe, and hit the bell button for more educational content.
Q & A
What is a conic section?
-A conic section is the intersection of a plane and a cone, which results in different shapes depending on the angle at which the plane slices the cone.
What are the four types of conic sections?
-The four types of conic sections are circles, ellipses, parabolas, and hyperbolas, which vary based on the angle of intersection between the plane and the cone.
What is the definition of a circle in geometry?
-A circle is defined as the set of all points in a plane that are equidistant from a fixed point called the center.
What is the constant distance from the center of a circle to any point on the circle called?
-The constant distance from the center of a circle to any point on the circle is called the radius.
What is the standard form of the equation of a circle?
-The standard form of the equation of a circle is (x - h)^2 + (y - k)^2 = r^2, where (h, k) is the center of the circle and r is the radius.
How do you find the equation of a circle with a center at the origin and a radius of 5 units?
-The equation of a circle with a center at the origin (0,0) and a radius of 5 units is x^2 + y^2 = 25.
What is the equation of a circle centered at (0, 3) with a radius of 6 units?
-The equation of a circle centered at (0, 3) with a radius of 6 units is x^2 + (y - 3)^2 = 36.
If the center of a circle is at (2, -5) and the radius is 10, what is the equation of the circle?
-The equation of a circle with a center at (2, -5) and a radius of 10 is (x - 2)^2 + (y + 5)^2 = 100.
What is the equation of a circle with a center at (1, 5) and a radius of √17 units?
-The equation of a circle with a center at (1, 5) and a radius of √17 units is (x - 1)^2 + (y - 5)^2 = 17.
How do you determine the equation of a circle given its center and radius?
-To determine the equation of a circle given its center (h, k) and radius r, use the formula (x - h)^2 + (y - k)^2 = r^2.
Why are some radii squared in the equations of circles?
-The radii are squared in the equations of circles because the standard form of the circle's equation involves the radius squared (r^2) to maintain the equation's balance and accurately represent the circle's size.
Outlines
📚 Introduction to Circles and Conic Sections
This paragraph introduces the topic of circles within the broader context of conic sections. It explains that a conic section is formed by the intersection of a plane and a cone, and that the angle of intersection results in four different types of conic sections. The focus then narrows down to circles, defining them as the set of all points on a plane equidistant from a fixed point, known as the center. The constant distance from the center to any point on the circle is termed the radius. The standard form of the equation of a circle is introduced as \( (x - h)^2 + (y - k)^2 = r^2 \), where \( (h, k) \) are the coordinates of the center and \( r \) is the radius.
🔍 Finding the Equation of a Circle
The second paragraph delves into how to derive the equation of a circle given its center and radius. It provides several examples to illustrate the process. The first example shows how to write the equation for a circle with its center at the origin and a radius of five units, resulting in the equation \( x^2 + y^2 = 25 \). Subsequent examples demonstrate the equation derivation for circles centered at various points, such as (0, 3) with a radius of six, (2, -5) with a radius of ten, and (1, 5) with a radius of \( \sqrt{17} \). Each example applies the standard form of the circle's equation by substituting the appropriate values for \( h \), \( k \), and \( r \).
🧮 Advanced Circle Equations with Non-Integer Radii
This paragraph addresses the calculation of circle equations when the radius is not a simple whole number. It begins with an example of a circle centered at (1, 5) with a radius of the square root of 17, emphasizing the process of substituting the center coordinates and the radius into the standard equation. The paragraph also includes an example where the circle's equation is given as \( x^2 + y^2 = 64 \), deducing that the radius is 8 based on the value of \( r^2 \). Another example involves a circle with an equation \( x^2 + (y - 2)^2 = 49 \), indicating a center at (0, 2) and a radius of 7. The discussion highlights the need to interpret non-integer values, such as the square root of 19, in the context of the circle's equation.
📈 Complex Circle Equations and Conclusion
The final paragraph tackles more complex circle equations, including those with negative coordinates and non-integer radii. It provides an example of a circle with a center at (-7, 5) and a radius of \( 2\sqrt{14} \), showing how to derive the equation from the given center and radius values. The paragraph also discusses how to interpret and simplify square roots in the context of circle equations, such as \( \sqrt{56} \) which simplifies to \( 2\sqrt{14} \). The video concludes with a reminder to like, subscribe, and activate notifications for more video tutorials, encouraging viewers to continue learning about mathematics through the channel's future content.
Mindmap
Keywords
💡Conic Section
💡Circle
💡Center
💡Radius
💡Standard Form
💡Equation
💡Origin
💡Coordinate System
💡Equidistant
💡Square Root
Highlights
Introduction to conic sections and the definition and equation of a circle.
A circle is defined as all points equidistant from a fixed point called the center.
The distance from the center to any point on the circle is constant and is called the radius.
The standard form of the equation of a circle is (x-h)^2 + (y-k)^2 = r^2.
Finding the equation of a circle with center at the origin and a radius of five units.
Example of writing the equation of a circle centered at (0,3) with a radius of six units.
Demonstration of deriving the equation of a circle with center at (2, -5) and a radius of ten units.
Explanation of how to find the equation of a circle with center at (1, 5) and a radius of √17 units.
Example of a circle with center at the origin and a radius of eight units, with the equation x^2 + y^2 = 64.
Illustration of the equation x^2 + y^2 = 19 for a circle centered at the origin.
How to write the equation for a circle with center (0,2) and a radius of √49 units.
Deriving the equation for a circle with center (-7,5) and a radius of 2√14 units.
The importance of understanding the relationship between the center, radius, and equation of a circle.
The video provides a comprehensive guide on how to find the equation of a circle given its center and radius.
The tutorial emphasizes the mathematical concepts behind the standard form of a circle's equation.
Encouragement for viewers to like, subscribe, and hit the bell button for more video tutorials.
Transcripts
Browse More Related Video

EQUATION OF CIRCLE IN STANDARD FORM | PROF D
Graphing Conic Sections Part 1: Circles

CIRCLE | TRANSFORMING GENERAL FORM TO STANDARD FORM | PROF D

CIRCLE | TRANSFORMING STANDARD FORM TO GENERAL FORM | PROF D

STANDARD EQUATION OF A CIRCLE IN A GENERAL FORM

How to find the standard form of the circle | Circle | Conic Section | Pre-Calculus
5.0 / 5 (0 votes)
Thanks for rating: