Average Rate of Change of a Function Over an Interval

The Organic Chemistry Tutor

10 Feb 201805:01

EducationalLearning

32 Likes 10 Comments

TLDRIn this lesson, the focus is on calculating the average rate of change of a function over an interval. The formula used is (f(b) - f(a)) / (b - a). Examples include finding the average rate of change for the functions f(x) = x^2 + 4x - 5 from x = 1 to x = 3, and f(x) = x^3 - 4 from x = 2 to x = 5. The lesson explains that this calculation represents the slope of the secant line between two points on a graph. The video also offers additional resources for pre-calculus, algebra, calculus, chemistry, and physics.

Takeaways

🧮 The lesson focuses on calculating the average rate of change of a function over an interval.
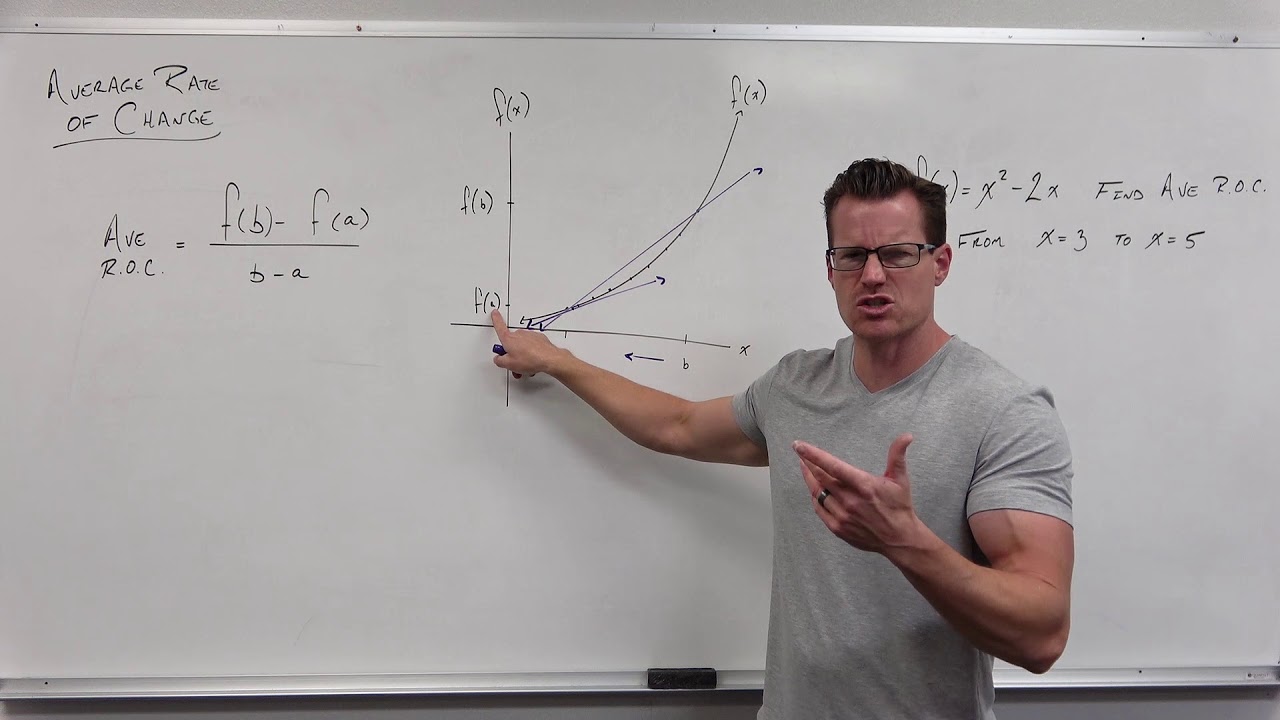
📊 The formula for the average rate of change is (f(b) - f(a)) / (b - a) where a and b are x-values, and f(a) and f(b) are the corresponding y-values.
🔍 To find f(a) and f(b), substitute a and b into the function. For example, if a = 1 and b = 3 in the function f(x) = x^2 + 4x - 5, then f(1) = 0 and f(3) = 16.
✏️ The average rate of change for the interval [1, 3] is (f(3) - f(1)) / (3 - 1) = 8, which represents the slope of the secant line.
📈 A secant line touches two points on a graph, while a tangent line touches only one point.
📝 Example 2: Calculate the average rate of change for f(x) = x^3 - 4 from x = 2 to x = 5. Here, a = 2 and b = 5.
🔢 Calculate f(5) and f(2) using the function: f(5) = 125 - 4 = 121, and f(2) = 8 - 4 = 4.
📉 The average rate of change for the interval [2, 5] is (f(5) - f(2)) / (5 - 2) = 39.
🧠 The average rate of change gives the slope of the secant line over the interval.
🔗 For more videos on pre-calculus, algebra, calculus, chemistry, and physics, check out the channel for additional helpful content.

Q & A

What is the formula for calculating the average rate of change of a function over an interval?
-The formula for calculating the average rate of change is (f(b) - f(a)) / (b - a) where a and b are the x-values, and f(a) and f(b) are the corresponding y-values.
How do you interpret the values 'a' and 'b' in the context of the average rate of change?
-In the context of the average rate of change, 'a' and 'b' represent the x-values of the interval over which you are calculating the rate of change.
What are f(a) and f(b) in the formula for the average rate of change?
-In the formula for the average rate of change, f(a) and f(b) represent the y-values corresponding to the x-values 'a' and 'b'.
How do you calculate f(1) for the function f(x) = x^2 + 4x - 5?
-To calculate f(1), substitute 1 into the equation: f(1) = 1^2 + 4*1 - 5, which simplifies to 1 + 4 - 5 = 0. So, f(1) = 0.
What is f(3) for the function f(x) = x^2 + 4x - 5?
-To calculate f(3), substitute 3 into the equation: f(3) = 3^2 + 4*3 - 5, which simplifies to 9 + 12 - 5 = 16. So, f(3) = 16.
How do you find the average rate of change for the function f(x) = x^2 + 4x - 5 on the interval [1, 3]?
-The average rate of change is calculated as (f(3) - f(1)) / (3 - 1). Given f(3) = 16 and f(1) = 0, the calculation is (16 - 0) / (3 - 1) = 16 / 2 = 8.
What does the average rate of change represent graphically?
-Graphically, the average rate of change represents the slope of the secant line that intersects the graph of the function at two points corresponding to the interval's endpoints.
What is the difference between a secant line and a tangent line on a graph?
-A secant line intersects the graph of a function at two points, while a tangent line touches the graph at only one point.
How do you calculate the average rate of change for f(x) = x^3 - 4 from x = 2 to x = 5?
-First, calculate f(5) = 5^3 - 4 = 125 - 4 = 121. Then, calculate f(2) = 2^3 - 4 = 8 - 4 = 4. The average rate of change is (f(5) - f(2)) / (5 - 2) = (121 - 4) / 3 = 117 / 3 = 39.
What are the steps to find f(5) and f(2) for the function f(x) = x^3 - 4?
-To find f(5), substitute 5 into the equation: f(5) = 5^3 - 4, which equals 125 - 4 = 121. To find f(2), substitute 2 into the equation: f(2) = 2^3 - 4, which equals 8 - 4 = 4.

Outlines

00:00

📐 Understanding Average Rate of Change

This lesson focuses on calculating the average rate of change of a function over an interval. The formula provided is (f(b) - f(a)) / (b - a) for the interval [a, b], where 'a' and 'b' are x-values, and f(a) and f(b) are their corresponding y-values. The example used involves calculating the average rate of change for a function from x = 1 to x = 3.

🔢 Step-by-Step Calculation of f(a) and f(b)

To calculate f(a) and f(b), we start with a = 1 and b = 3. By substituting these values into the function, we find that f(1) = 0 and f(3) = 16. These calculations are broken down step-by-step, demonstrating the process of substituting and simplifying to find the y-values for these x-values.

📊 Computing the Average Rate of Change

Using the values f(1) = 0 and f(3) = 16, the average rate of change is calculated as (16 - 0) / (3 - 1) = 8. This result represents the slope of the secant line for the function over the interval [1, 3].

📈 Graphical Representation of Secant Line

A generic graph is plotted to illustrate the concept of the secant line, which touches two points on a graph. The secant line's slope represents the average rate of change, as opposed to a tangent line, which only touches one point on a graph.

📐 Calculating Average Rate of Change for Another Function

The lesson moves to another example involving the function f(x) = x³ - 4, and finding the average rate of change from x = 2 to x = 5. The steps involve calculating f(5) and f(2) and then finding the difference quotient to determine the average rate of change.

🔢 Step-by-Step Calculation for f(5) and f(2)

For the function f(x) = x³ - 4, f(5) is calculated as 121 and f(2) as 4. These values are found by substituting x = 5 and x = 2 into the function and simplifying the results.

📊 Final Calculation of Average Rate of Change

Using the values f(5) = 121 and f(2) = 4, the average rate of change is calculated as (121 - 4) / (5 - 2) = 39. This calculation shows the steps involved in determining the average rate of change over the interval [2, 5].

🎓 Conclusion and Additional Resources

The lesson concludes by summarizing how to calculate the average rate of change of a function. It also provides information about additional videos on pre-calculus, algebra, calculus, chemistry, and physics available on the channel for further learning.

Mindmap

Keywords

💡Average Rate of Change

The average rate of change is a measure of how a function's value changes between two points. It is calculated using the formula (f(b) - f(a)) / (b - a), where 'a' and 'b' are x-values. In the video, this concept is demonstrated through examples involving specific functions and intervals, illustrating how to find the average rate of change over given ranges.

💡Secant Line

A secant line is a straight line that intersects a curve at two points. The slope of this line represents the average rate of change of the function between those points. In the video, the secant line is introduced to explain how the average rate of change corresponds to the slope of this line on a graph.

💡Interval

An interval refers to the range between two points on the x-axis, typically denoted as [a, b]. It is essential for calculating the average rate of change of a function. The video uses intervals such as [1, 3] and [2, 5] to demonstrate how to calculate changes in function values within those ranges.

💡Function

A function is a mathematical relationship where each input (x-value) is related to exactly one output (y-value). The video uses functions like f(x) = x^2 + 4x - 5 and f(x) = x^3 - 4 to show how to compute values and rates of change for different inputs.

💡Slope

The slope is a measure of the steepness or incline of a line. It is calculated as the ratio of the change in y-values to the change in x-values. In the context of the video, the slope of the secant line represents the average rate of change of the function over a specific interval.

💡f(a) and f(b)

These notations represent the function's values at specific points 'a' and 'b' respectively. In the video, f(a) and f(b) are calculated for different functions to determine the average rate of change over the interval [a, b].

💡Calculation

Calculation refers to the process of determining values through mathematical operations. The video involves several calculations, such as finding f(a) and f(b), squaring numbers, and dividing differences, to illustrate the average rate of change.

💡Tangent Line

A tangent line is a straight line that touches a curve at exactly one point. It represents the instantaneous rate of change at that point, contrasting with the secant line, which touches at two points. The video briefly mentions the tangent line to differentiate it from the secant line.

💡x-values

X-values are the inputs or independent variables in a function. They are crucial for calculating the average rate of change, as the formula relies on the difference between x-values (b - a). The video uses x-values like 1, 3, 2, and 5 in its examples.

💡y-values

Y-values are the outputs or dependent variables in a function, denoted as f(a) and f(b) in the video. They are calculated by plugging x-values into the function. The differences between y-values are used to find the average rate of change.

Highlights

Lesson focuses on calculating the average rate of change of a function over an interval.

Formula for average rate of change is f(b) - f(a) / (b - a) on the interval a to b.

a and b are x values, f(a) and f(b) are the corresponding y values.

Example calculation with a=1, b=3, and the function f(x) = x^2 + 4x - 5.

f(1) calculated as 0 using the given function.

f(3) calculated as 16 using the given function.

Average rate of change from x=1 to x=3 is 8, representing the slope of the secant line.

Secant line touches two points on a graph, unlike a tangent line that touches one.

Graphical representation of the concept with a generic graph.

Explanation of how to find the average rate of change between points a and b.

Second example with the function f(x) = x^3 - 4 and interval from x=2 to x=5.

Calculation of f(5) as 121 and f(2) as 4.

Average rate of change from x=2 to x=5 is 39.

The average rate of change indicates how a function changes over an interval.

Additional resources available for pre-calculus, algebra, calculus, chemistry, and physics.

Transcripts

Browse More Related Video

Introduction to Average Rate of Change

Introduction to the Difference Quotient

AP CALCULUS AB 2022 Exam Full Solution FRQ#3(a,b)

Mean Value Theorem with Example

Average Rate of Change of a Function (Precalculus - College Algebra 11)

Decomposing Functions - Composition of Functions