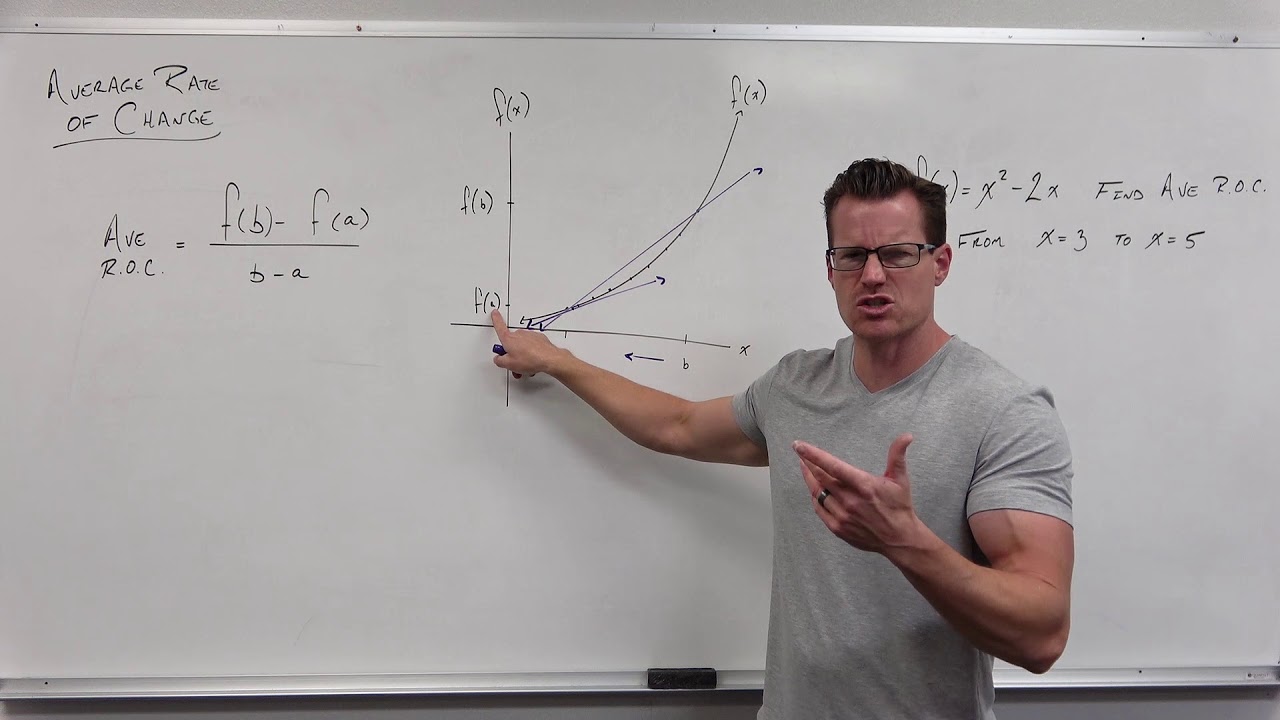
Introduction to Average Rate of Change
TLDRThe video script delves into the concept of average rate of change (AROC) within a function's graph. It illustrates how to calculate AROC by taking two points on the graph, labeled as 'a' and 'b', and finding the difference in their function values (f(b) - f(a)) divided by the difference in their x-values (b - a). This formula is analogous to the slope formula between two points, indicating that the secant line connecting these points represents the AROC. A practical example is provided using the function f(x) = x^2 + 1 over the interval from 2 to 5, resulting in an AROC of 7. The script emphasizes the dual significance of (f(b) - f(a)) / (b - a) as both the AROC over the interval and the slope of the secant line, setting the stage for further mathematical exploration.
Takeaways
- 📈 The concept of average rate of change (AROC) is introduced, which is the rate at which a function value changes over an interval.
- 🔢 AROC is calculated by finding the difference between the function values at two points (f(b) - f(a)) and dividing it by the difference in their x-values (b - a).
- 📊 AROC is represented using interval notation, often denoted as [a, b], indicating the interval over which the rate of change is calculated.
- 📐 The formula for AROC is similar to the slope formula between two points, which is why AROC can also be thought of as the slope of a secant line.
- 🔑 The term f(b) - f(a) / (b - a) has two meanings: it is both the AROC over the interval [a, b] and the slope of the secant line between the points.
- 💡 The secant line, which connects two points on a function, represents the average rate of change over the interval between those points.
- 🌠 The slope of the secant line provides a visual representation of how steeply the function is increasing or decreasing over a particular interval.
- 📚 To find the AROC without graphing, you can directly apply the AROC formula using the given x-values and the corresponding function values.
- 📘 An example is provided using the function f(x) = x^2 + 1 over the interval from 2 to 5, demonstrating how to calculate the AROC.
- 🧮 The calculation for the example results in an AROC of 7, which means the function value increases by an average of 7 units over each unit change in x over the interval [2, 5].
- 🔍 Understanding the AROC and its relationship to the slope of a secant line is crucial for further mathematical concepts that will be explored in future lessons.
Q & A
What is the concept of average rate of change (AROC)?
-The average rate of change (AROC) is a measure of how a function value changes over an interval. It is calculated by taking the difference between the function values at two points on the graph, dividing it by the difference between the x-values of those points.
How is the average rate of change formula similar to the slope formula?
-The average rate of change formula is similar to the slope formula because both involve the difference in y-values (function values) divided by the difference in x-values. This similarity means that the average rate of change between two points on a function is equal to the slope of the line (secant line) between those points.
What is a secant line?
-A secant line is a straight line that intersects a function at two or more points. In the context of the script, it refers to the line drawn between two points on a function, representing the average rate of change over that interval.
What does the term 'f(b) - f(a)' represent in the context of the average rate of change?
-In the context of the average rate of change, 'f(b) - f(a)' represents the difference in function values between two points 'a' and 'b' on the graph of a function. When divided by 'b - a', it gives the average rate of change over the interval from 'a' to 'b' and also the slope of the secant line between these points.
How do you calculate the average rate of change for the function f(x) = x^2 + 1 over the interval from x = 2 to x = 5?
-To calculate the average rate of change, you substitute x = 5 into the function to get f(5) = 5^2 + 1 = 26, and x = 2 to get f(2) = 2^2 + 1 = 5. Then you find the difference f(5) - f(2) = 26 - 5 = 21, and divide by the difference in x-values, which is 5 - 2 = 3. The average rate of change is therefore 21 / 3 = 7.
What is the slope of the secant line for the function f(x) = x^2 + 1 over the interval from x = 2 to x = 5?
-The slope of the secant line, which is the same as the average rate of change for this interval, is calculated to be 7, as determined in the previous answer.
Why is it important to understand the concept of average rate of change?
-Understanding the concept of average rate of change is important because it provides insight into how a function's value changes over a specific interval. It is a fundamental concept in calculus and is used to analyze various real-world phenomena that involve change over time or distance.
What are the two main interpretations of the formula f(b) - f(a) / (b - a)?
-The two main interpretations are: 1) It is the average rate of change of the function over the interval from 'a' to 'b', and 2) It is the slope of the secant line over the interval from 'a' to 'b'.
How does the average rate of change relate to the slope of a tangent line?
-The average rate of change is an approximation of the instantaneous rate of change, which is the slope of the tangent line at a specific point. As the interval between 'a' and 'b' becomes smaller, the average rate of change approaches the slope of the tangent line at the point 'a'.
What is the significance of the interval notation [a, b] in the context of average rate of change?
-The interval notation [a, b] signifies the specific section of the function over which the average rate of change is being calculated. It helps to clearly define the domain within which the function's behavior is being analyzed.
Can the average rate of change be negative?
-Yes, the average rate of change can be negative if the function value at point 'b' is less than the function value at point 'a', indicating that the function is decreasing over the interval from 'a' to 'b'.
What happens to the average rate of change if the function is constant over an interval?
-If the function is constant over an interval, meaning the function value does not change, then the average rate of change over that interval will be zero. This is because there is no difference in the function values (f(b) - f(a) = 0).
How does the average rate of change formula help in understanding the behavior of a function?
-The average rate of change formula helps in understanding the behavior of a function by quantifying how the function's output changes with respect to changes in its input over a given interval. This can indicate whether the function is generally increasing or decreasing, and at what rate.
Outlines
📈 Understanding Average Rate of Change
The first paragraph introduces the concept of average rate of change (AROC) in the context of a function's graph. It explains that by taking two points on the graph (with x values a and b) and calculating the difference in function values (f(b) - f(a)) divided by the difference in x values (b - a), we get the AROC. This formula is analogous to the slope formula between two points, indicating that the secant line between these points represents the AROC. The paragraph also clarifies that f(b) - f(a) / (b - a) has two meanings: it's both the AROC over the interval from a to b and the slope of the secant line over the same interval. An example is provided using the function f(x) = x^2 + 1 over the interval from 2 to 5, illustrating how to apply the AROC formula without graphing.
🔍 Calculating the Average Rate of Change
The second paragraph focuses on calculating the average rate of change for the function f(x) = x^2 + 1 between the points x = 2 and x = 5. It walks through the process of substituting the x values into the function to find the function values at these points, then using these values in the AROC formula to find the slope of the secant line over the specified interval. The calculation yields an AROC of 7, which is also the slope of the secant line between x = 2 and x = 5. The paragraph emphasizes the importance of understanding the formula's interpretation and sets the stage for further concepts to be explored in future videos.
Mindmap
Keywords
💡Average Rate of Change (AROC)
💡Function
💡Graph
💡Secant Line
💡Slope
💡Interval Notation
💡X and Y values
💡Function Value
💡Miscellaneous Function
💡Point
💡Divide
Highlights
The concept of average rate of change (AROC) is introduced.
A function is represented graphically, and two points on the graph are identified as a and b.
The function values at points a and b are defined as f(a) and f(b) respectively.
The average rate of change is calculated by the difference in function values divided by the difference in x-values.
AROC is abbreviated as AROC and is represented over the interval a, b using interval notation.
The formula for AROC is shown to be similar to the slope formula between two points.
The slope formula is m = (change in y) / (change in x), which is analogous to AROC.
The line between two points on a function graph is called a secant line.
The slope of the secant line represents the average rate of change over the interval from a to b.
The expression f(b) - f(a) / (b - a) has two meanings: AROC and the slope of the secant line.
An example function f(x) = x^2 + 1 is used to demonstrate the calculation of AROC.
The interval from x = 2 to x = 5 is chosen for the example.
The function is evaluated at x = 5 and x = 2 to find f(5) and f(2).
The average rate of change for the interval is calculated to be 7.
The slope of the secant line for the given function and interval is also determined to be 7.
The two interpretations of the formula f(b) - f(a) / (b - a) are emphasized as key takeaways.
The implications of understanding AROC and secant line slope will lead to further concepts in future videos.
Transcripts
Browse More Related Video

Average Rate of Change of a Function Over an Interval

Introduction to the Difference Quotient
Average Rate of Change of a Function (Precalculus - College Algebra 11)

Calculus 1 Lecture 3.2: A BRIEF Discussion of Rolle's Theorem and Mean-Value Theorem.

1.3 - Average Rates of Change

Average Value of a Function
5.0 / 5 (0 votes)
Thanks for rating: