How To Solve Word Problems of Any Kind . Nutshell maths-2

mathOgenius
16 Jan 202206:54
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers a step-by-step guide on solving word problems, specifically focusing on linear equations. It begins with the importance of reading and understanding the problem statement, identifying unknowns, and assigning symbols to them. The script uses a problem involving Jacob and his son's ages to illustrate the process. It emphasizes the need to avoid common traps in word problems and the necessity of having as many equations as there are unknowns. The video demonstrates converting the word problem into mathematical equations, using the elimination method to solve the system of equations, and finding the solution. The presenter encourages viewers to practice and promises more specific videos if the response is positive, highlighting that math is integral to problem-solving.

Takeaways
  • 📚 The video is focused on teaching how to approach and solve word problems using mathematics.
  • 🔍 The importance of reading and understanding the question carefully is emphasized to avoid common traps in word problems.
  • 👤 The video uses a specific word problem involving Jacob and his son's ages to demonstrate the solving process.
  • 📝 Assigning symbols to unknowns is a crucial first step in converting a word problem into a mathematical equation.
  • ⚠️ A reminder that word problems often contain traps that require careful reading and understanding.
  • 🔢 The script outlines the process of setting up two equations based on the information provided in the word problem.
  • 🔄 The necessity of having the same number of equations as the number of unknowns to solve a problem is highlighted.
  • 🧩 The video demonstrates the elimination method as a way to solve the system of linear equations.
  • 📉 Simplifying equations and carefully subtracting them to eliminate variables is shown as part of the solving process.
  • 🎯 The final step involves substituting the found value of one variable into an equation to solve for the other.
  • 🎉 The video concludes with the solution that Jacob is currently 40 years old and his son is 10 years old.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is solving word problems, specifically focusing on linear equations.

  • What is the general approach to solving word problems as discussed in the video?

    -The general approach to solving word problems involves reading the question carefully, identifying unknowns, assigning symbols to them, and converting the word problem into a mathematical equation which can then be solved.

  • What is the first step in solving any math problem according to the video?

    -The first step in solving any math problem is to read the question carefully.

  • What is the example word problem presented in the video?

    -The example word problem is about Jacob and his son's ages. It states that five years from now Jacob's age will be three times his son's age, and five years ago Jacob's age was seven times his son's age.

  • What are the two unknowns in the example word problem?

    -The two unknowns in the example word problem are Jacob's present age (x) and his son's present age (y).

  • Why is it important to be cautious when converting word problems into mathematical equations?

    -It's important to be cautious because word problems often contain traps that can lead to incorrect equations if not read and understood carefully.

  • What is the correct equation representing the relationship between Jacob's and his son's ages five years from now?

    -The correct equation is x + 5 = 3(y + 5), which accounts for the increase in both Jacob's and his son's ages over the next five years.

  • How many equations are needed to solve for two variables in a word problem?

    -To solve for two variables, you need at least two independent equations.

  • What is the second equation derived from the information that Jacob's age was seven times his son's age five years ago?

    -The second equation is x - 5 = 7(y - 5), which represents the relationship between their ages five years ago.

  • What method does the video suggest to solve the system of equations presented in the word problem?

    -The video suggests using the elimination method to solve the system of equations.

  • What are the present ages of Jacob and his son according to the solution of the word problem?

    -According to the solution, Jacob's present age is 40 years, and his son's present age is 10 years.

  • What advice does the video give for approaching word problems in general?

    -The video advises to convert word problems into mathematical equations, look for enough information to form equations, and be aware of potential traps in the wording of the problems.

Outlines
00:00
📚 Introduction to Solving Word Problems

This paragraph introduces the concept of word problems and sets the stage for the video's educational content. The speaker acknowledges requests from the audience to create a video on word problems and mentions a common issue people face with linear equations. The video aims to teach the general approach to solving word problems through an example involving the ages of Jacob and his son. The speaker encourages viewers to pause and attempt the problem before revealing the solution. The paragraph emphasizes the importance of reading the problem carefully, identifying unknowns, and translating the word problem into a mathematical equation. A specific word problem is presented, involving the ages of Jacob and his son, with the goal of finding their present ages based on given conditions about their ages five years from now and five years ago.

05:02
🔍 Detailed Explanation and Solution of a Word Problem

In this paragraph, the speaker provides a step-by-step guide on how to approach and solve the word problem presented earlier. The process begins with reading the problem carefully to identify the unknowns and their relationships, which are then translated into mathematical equations. The speaker illustrates a common mistake to avoid, emphasizing the importance of understanding the time aspect of the problem (adding five years to both Jacob's and his son's ages). Two equations are derived from the problem statement, which are then simplified and solved using the elimination method. The solution process involves subtracting one equation from the other to eliminate the variable x, solving for y, and then substituting y back into one of the original equations to find x. The paragraph concludes with the solution that Jacob is currently 40 years old and his son is 10 years old. The speaker also encourages viewers to look for additional information in word problems if there are more unknowns than equations and hints at creating more specific word problem videos based on audience feedback.

Mindmap
Keywords
💡Word Problems
Word problems are a type of mathematical problem that requires understanding a narrative or statement and then applying mathematical concepts to find a solution. In the video, word problems are the central theme, with the host focusing on teaching viewers how to approach and solve them. An example from the script is the age-related problem involving Jacob and his son, which requires setting up and solving equations based on the information provided.
💡Linear Equations
Linear equations are algebraic equations of the first degree, representing a straight line when graphed. The video specifically addresses linear equations as a common type of word problem that people struggle with. The problem involving Jacob's and his son's ages is an example of a linear equation, where the relationship between their ages is expressed as x + 5 = 3(y + 5) and x - 5 = 7(y - 5).
💡Unknowns
In the context of the video, unknowns refer to the variables or quantities that are not known and need to be determined through the problem-solving process. The script mentions assigning symbols to unknowns, such as Jacob's present age (x) and his son's present age (y), which are then used to set up equations that will help find their values.
💡Symbols
Symbols in mathematics are used to represent unknown quantities or variables. The video script illustrates this by assigning the symbol 'x' to represent Jacob's present age and 'y' to represent his son's present age. These symbols are crucial for translating the word problem into a mathematical equation.
💡Equations
Equations are mathematical statements that assert the equality of two expressions. In the video, equations are used to represent the relationships between the ages of Jacob and his son. The script includes two equations derived from the word problem: x + 5 = 3y + 15 and x - 7y - 30 = 0, which are essential for solving the problem.
💡Traps
Traps in word problems refer to common mistakes or misunderstandings that can lead to incorrect solutions. The video emphasizes the importance of carefully reading and understanding the problem to avoid these traps. An example from the script is the mistake of not accounting for the son's age increasing in five years, which would incorrectly lead to the equation x + 5 = 3y.
💡Elimination Method
The elimination method is a technique used to solve systems of linear equations by adding or subtracting the equations to eliminate one variable. In the video, the host uses the elimination method to solve for the ages of Jacob and his son. The script demonstrates this by subtracting the second equation from the first to eliminate x and solve for y.
💡Substitution
Substitution is another method for solving systems of equations, where one variable is expressed in terms of another and then substituted into the other equation. Although not explicitly used in the script's example, the video mentions substitution as one of the methods to solve linear equations, suggesting its relevance in different contexts.
💡Cross Multiplication
Cross multiplication is a technique used to solve proportions or to eliminate fractions in equations by multiplying both sides of an equation by the denominators of the fractions. The video briefly mentions cross multiplication as a method to solve equations, although it is not used in the script's example problem.
💡Solving Word Problems
Solving word problems involves translating a narrative or statement into a mathematical equation or set of equations and then finding the solution. The video's main focus is on teaching viewers how to approach and solve word problems, such as the age-related problem with Jacob and his son. The script demonstrates the step-by-step process of solving such problems, emphasizing the importance of careful reading and understanding.
Highlights

The video focuses on teaching how to approach and solve word problems using mathematics.

The presenter received many requests to make a video on word problems, particularly linear equations.

The chosen example is a simple linear equation word problem involving Jacob and his son's ages.

The importance of reading the question carefully to identify unknowns and their relationships is emphasized.

Assigning symbols to unknowns is the first step in converting a word problem into a mathematical equation.

The video warns about the common traps in word problems and the need to understand the context correctly.

The example given involves creating equations based on Jacob's age in relation to his son's age in different time frames.

Two equations are derived from the problem statement, one for the present and one for five years ago.

The necessity of having n equations for n unknowns in solving word problems is explained.

The presenter demonstrates the elimination method to solve the system of linear equations.

The process of simplifying and subtracting equations to isolate variables is shown step by step.

The solution reveals that Jacob's son is currently 10 years old.

Using the value of one variable, the presenter solves for the other variable, finding Jacob's age to be 40.

The video concludes by summarizing the steps taken to solve the word problem and encourages further learning.

The presenter invites feedback and suggestions for more specific word problem videos in the future.

The video ends with a reminder of the importance of math in everyday life.

Transcripts

Browse More Related Video

Algebra SYSTEM WORD PROBLEM – Let’s solve it step-by-step...

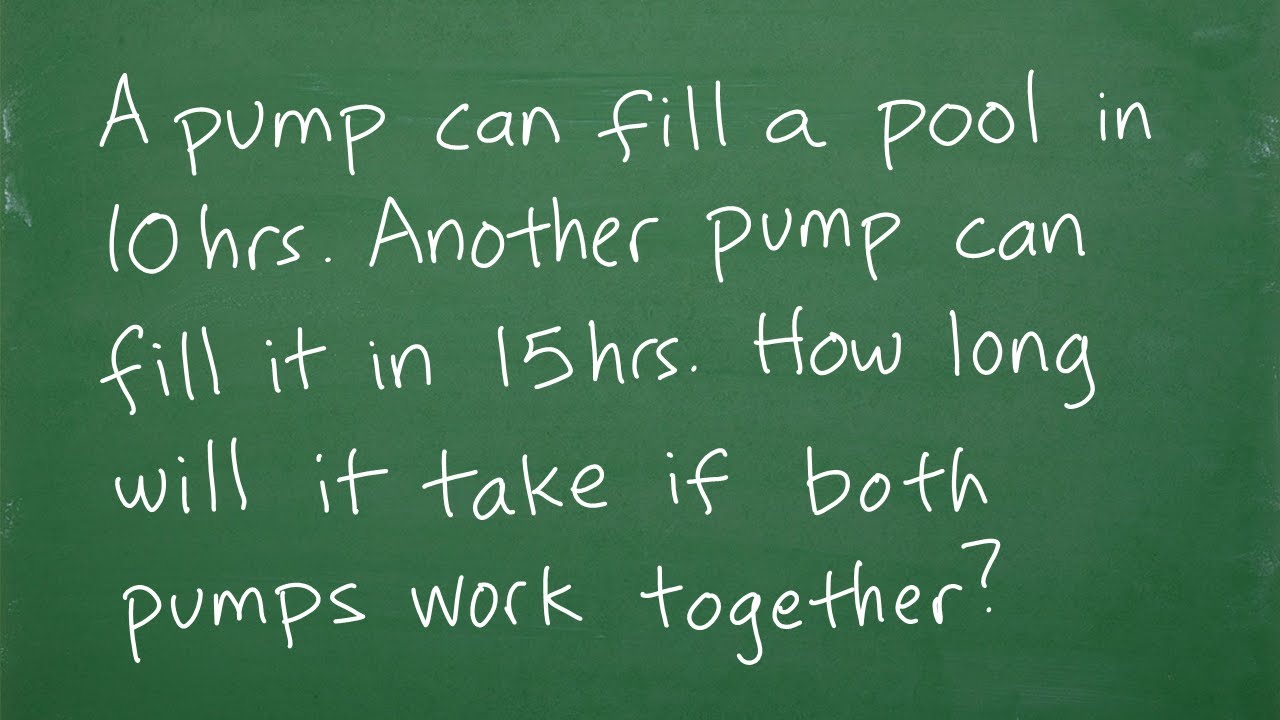
A pump can fill a pool in 10hrs. Another pump can fill it in 15hrs. Both pumps together will take?

Solving Systems of Equations With 3 Variables & Word Problems

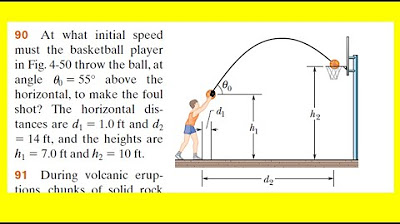
How to solve any projectile motion question

Ch. 1.7 Modeling with Equations

How many oz of 5% acid and 20% acid must be mixed to get 10 oz of a solution that is 12.5% acid?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Word ProblemsLinear EquationsMath TutorialProblem SolvingMath SkillsEducational VideoMath TipsStudent HelpAlgebraLearning