How to solve any projectile motion question
TLDRThis video script outlines a step-by-step method for solving projectile motion problems. It begins by illustrating the importance of visualizing the problem with a drawing and establishing a coordinate system. The script then details the process of filling in known values into a table and using standard equations to solve for unknowns in both horizontal and vertical directions independently. The method is demonstrated with a simple example and further explained with a more complex scenario involving a basketball throw. The key to solving these problems is understanding how to treat the horizontal and vertical components separately and apply the appropriate equations to find the solution.
Takeaways
- 🎯 The first step in solving projectile motion problems is to draw a diagram of the scenario.
- 📐 Superimpose an XY coordinate system onto the diagram to help visualize the motion.
- 🔢 Fill in a table with known values such as initial and final coordinates, velocities, accelerations, and time.
- 🌟 Remember that the horizontal initial velocity is given by the initial velocity multiplied by the cosine of the launch angle, and the vertical initial velocity by the initial velocity multiplied by the sine of the launch angle.
- 🚫 The acceleration in the horizontal direction is zero due to no horizontal force acting on the projectile, while in the vertical direction, it is consistently -9.8 m/s² due to gravity.
- 🕒 The time used for the horizontal motion is the same as that for the vertical motion, as they are independent of each other.
- 📱 Use a set of standard equations to solve for unknowns in both horizontal and vertical directions independently.
- 📈 For the horizontal direction, use the equation X = Vx_initial * time + (1/2) * ax * time², where ax is zero.
- 📊 For the vertical direction, use the equation Y = Vy_initial * time - (1/2) * ay * time², where ay is -9.8 m/s².
- 🔄 To find the final speed at a certain point, combine the horizontal and vertical velocities using vector addition and the Pythagorean theorem.
- 🛑 The process can be more complex when the launch point is not at ground level, requiring adjustments to the initial coordinates and potentially more complex algebraic manipulations to solve for unknowns.
Q & A
What is the first step in solving a projectile motion problem?
-The first step is to draw a picture of the scenario to help visualize the problem.
How do you set up the coordinate system for a projectile motion problem?
-You should superimpose an XY coordinate system onto the picture, typically placing the origin at the point from which the projectile is launched.
What information should be filled into the table during step three of the process?
-Step three involves filling in all known information, such as initial and final coordinates, initial and final velocities, accelerations, and time into a table.
What is the significance of the horizontal and vertical components of the initial velocity in projectile motion?
-The horizontal component of the initial velocity is given by the initial velocity multiplied by the cosine of the launch angle, while the vertical component is given by the initial velocity multiplied by the sine of the launch angle.
How does gravity affect the acceleration in the vertical direction during projectile motion?
-Gravity affects the acceleration in the vertical direction by causing it to be negative 9.8 meters per second squared, as it accelerates the projectile downward.
What is the process for solving for unknowns in the horizontal and vertical directions in projectile motion?
-In step four, you use a standard set of equations to solve for unknowns in both the horizontal and vertical directions independently of one another.
How can you find the final x-coordinate in a projectile motion problem?
-You can find the final x-coordinate using the equation X = Vx_initial * time + (1/2) * ax * time^2, where Vx_initial is the initial horizontal velocity, ax is the acceleration in the x-direction (which is 0 for horizontal motion), and time is the duration of the projectile's flight.
What is the method to calculate the height (H) reached by the projectile in the vertical direction?
-The height (H) can be calculated using the equation H = Vy_initial * time - (1/2) * ay * time^2, where Vy_initial is the initial vertical velocity and ay is the acceleration due to gravity (negative 9.8 m/s^2).
How do you determine the final speed of the projectile just before impact?
-To determine the final speed at impact, you need to consider both the horizontal and vertical components of the velocity. Use the Pythagorean theorem to find the resultant velocity by adding the squares of the horizontal and vertical velocities and taking the square root of the sum.
What is the role of trigonometry in solving projectile motion problems?
-Trigonometry plays a crucial role in calculating the horizontal and vertical components of the initial velocity, as well as in finding the final speed at impact by using relationships like sine, cosine, and tangent of the launch angle.
How does the process of solving a projectile motion problem change when the launch is above ground level?
-When the launch is above ground level, the initial coordinates are not both zero. You must account for the initial height and horizontal distance in your calculations, adjusting the origin of your coordinate system accordingly.
Outlines
📏 Introduction to Projectile Motion Analysis
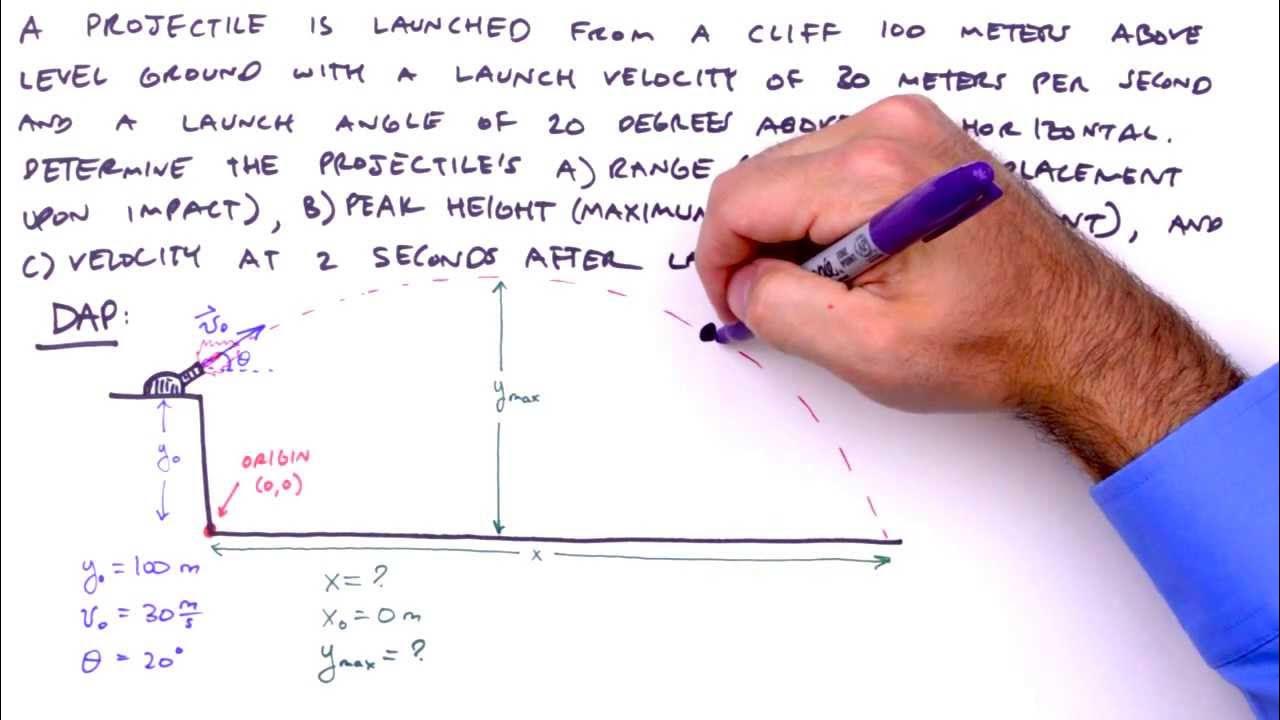
This paragraph introduces the process of solving projectile motion questions through a structured five-step method. It emphasizes the importance of visualizing the problem by drawing a picture, superimposing an XY coordinate system, filling in known values into a table, applying standard equations to solve for unknowns, and finally calculating the desired outcomes. The example used involves a stone projected from a cliff, and the steps are explained in the context of this scenario.
📐 Filling the Projectile Motion Table with Known Values
In this paragraph, the focus is on the third step of the projectile motion analysis, which involves filling in a table with known values related to the motion of the projectile. The table includes initial and final coordinates, initial and final velocities, accelerations, and time. The example continues with the stone projection, and the process of filling in the table is explained in detail, highlighting the importance of understanding the effects of gravity and the lack of horizontal acceleration.
🧮 Solving for Unknowns in Projectile Motion
This paragraph delves into the fourth step of the analysis, which is solving for unknowns in both the horizontal and vertical directions using a set of standard equations. The explanation is based on the given information from the previous steps, and it shows how to treat the horizontal and vertical directions independently. The process is demonstrated using the provided example, with a focus on solving for the final x-coordinate in the horizontal direction and the height (H) in the vertical direction.
🏀 More Challenging Projectile Motion Example
The paragraph presents a more complex example of projectile motion, involving a basketball player throwing a ball at a 55-degree angle. The process of drawing a picture, superimposing the coordinate system, and filling in the known values is reiterated, with the new scenario's specific details incorporated. The initial and final coordinates, as well as the angle of projection, are used to set up the equations for solving the unknown initial launch speed.
🔢 Completing the Projectile Motion Calculation
The final paragraph focuses on completing the calculations for the more challenging projectile motion example. It demonstrates how to solve for the unknown initial launch speed by setting up and manipulating the equations from the previous steps. The process involves solving for time first and then using that value to find the launch speed. The algebraic manipulation is shown in detail, leading to the final solution in feet per second.
Mindmap
Keywords
💡Projectile Motion
💡Coordinate System
💡Initial Velocity
💡Acceleration
💡Time of Flight
💡Final Velocity
💡Horizontal and Vertical Components
💡Trajectory
💡Impact Point
💡Pythagorean Theorem
Highlights
The video outlines a five-step process for solving projectile motion questions, providing a structured approach to tackle such problems.
The initial step involves drawing a picture to visualize the projectile motion scenario, which is crucial for understanding the problem.
Superimposing an XY coordinate system onto the picture is the second step, which helps in organizing the known and unknown values systematically.
Filling in all known information into a table is the third step, which lays the foundation for solving the problem with essential data.
The fourth step involves using a standard set of equations to solve for unknowns in both horizontal and vertical directions independently.
The video emphasizes the importance of treating horizontal and vertical directions as independent in projectile motion problems.
The method can be applied to various projectile motion questions by following the same four steps, showcasing its versatility.
The video provides a clear example of solving a projectile motion question, making it easier for viewers to grasp the concept.
It is highlighted that the initial velocity in the horizontal direction is the initial velocity multiplied by the cosine of the launch angle.
In the vertical direction, the acceleration due to gravity is always negative 9.8 meters per second squared, which is a key factor in solving such problems.
The time used in the horizontal direction should be the same as the time used in the vertical direction, which simplifies the calculations.
The final step involves calculating the final speed at a specific point, which requires understanding the vector nature of velocity in projectile motion.
The Pythagorean theorem is used to calculate the resultant velocity, demonstrating the application of mathematical principles in physics.
The video also addresses a more challenging example involving a basketball player throwing a ball, showcasing the adaptability of the method.
The process of establishing a good coordinate system is emphasized, which is crucial for accurately labeling initial and final coordinates.
The video concludes by reiterating the four-step process, reinforcing its effectiveness in solving projectile motion questions.
Transcripts
Browse More Related Video
How To Solve Any Projectile Motion Problem (The Toolbox Method)

Equations of Projectile Motion in Physics Explained - [1-4-6]

Substitution Method For Solving Systems of Linear Equations, 2 and 3 Variables, Algebra 2

AP Physics - Projectile Motion

How To Solve Word Problems of Any Kind . Nutshell maths-2

Physics 3.5.4h - Projectile Practice Problem 8
5.0 / 5 (0 votes)
Thanks for rating: