Ch. 1.7 Modeling with Equations
TLDRThis educational video script focuses on solving word problems using mathematical equations, often a challenging task for students. It outlines a step-by-step strategy for tackling such problems, emphasizing the importance of reading the problem thoroughly, identifying key variables, and drawing diagrams to visualize relationships. The script also covers common equations found in algebra, such as those for simple interest, mixtures, distance, and work rate, providing examples to illustrate the process. The goal is to ensure students not only find the variable's value but also apply it to answer the actual question posed.
Takeaways
- 📚 The lesson focuses on chapter 1.7, which is about modeling with equations and solving word problems.
- 🔍 Students often struggle with word problems, which are also known as application problems, and typically require answers in decimal form.
- 📉 The number of decimal places used in answers usually depends on the problem, with one or two decimal places being standard.
- 🔑 A guideline for solving word problems is to read the problem thoroughly multiple times to understand what is being asked and what information is relevant.
- 🧐 It's important to sift through the information to find the 'gold' or the key details necessary to solve the problem, ignoring irrelevant details.
- 📝 The problem-solving process involves identifying the variable(s), which is often indicated in the last sentence of the problem.
- 🎨 Drawing a picture can help visualize the problem, making it easier to understand relationships and formulate equations.
- ✏️ Labeling the picture with identified variables and relevant information is crucial for creating expressions and equations.
- 🔢 Keywords in word problems often have direct mathematical translations, such as 'more than' meaning addition and 'double' meaning multiplication.
- 📉 Common equations for application problems, like simple interest (I = prt) and mixtures (C = x/v), are provided to help solve specific types of problems.
- 🤔 After finding the value of the variable(s), it's essential to apply it to answer the actual question posed by the problem, not just stopping at finding the variable.
Q & A
What is the main focus of Chapter 1.7 in the transcript?
-The main focus of Chapter 1.7 is on modeling with equations, specifically dealing with word problems and different strategies for solving them.
Why are word problems often disliked by students?
-Word problems are often disliked by students because they are application problems that require interpreting the problem and translating it into mathematical equations, which can be challenging.
How many decimal places are typically used when solving word problems?
-Typically, one or two decimal places are used when solving word problems, depending on the problem and the presence of decimals in the equations.
What is the first guideline suggested for modeling with equations in the transcript?
-The first guideline is to read the problem all the way through before starting any calculations or drawing any pictures.
How many times should a word problem be read during the problem-solving process?
-A word problem should be read at least three times during the problem-solving process, with more readings for higher-level or less familiar problems.
What is the purpose of drawing a picture when solving word problems?
-Drawing a picture helps to visualize the problem, making it easier to understand the relationships and processes described in the word problem.
What is the general form of the equation for simple interest mentioned in the transcript?
-The general form of the equation for simple interest is I = P * r * t, where I is the interest earned, P is the principal amount, r is the rate of interest, and t is the time in years.
What is the significance of identifying the variable in word problems?
-Identifying the variable is significant because it represents the unknown value or the quantity that the problem is asking to find, which is central to solving the problem.
How can keywords in word problems be used to form mathematical equations?
-Keywords in word problems often have direct translations into mathematical symbols, such as 'more than' meaning addition, 'double' meaning multiplication by two, and 'less than' meaning subtraction.
What is the importance of answering the actual question proposed in a word problem?
-It is important to answer the actual question because solving for the variable may not directly provide the final answer; the value of the variable often needs to be applied in an additional step to answer the specific question asked.
Can you provide an example of a common equation used in application problems from the transcript?
-An example of a common equation used in application problems is the distance formula, d = r * t, where d is the distance, r is the rate of travel, and t is the time.
Outlines
📚 Introduction to Word Problem Modeling
This paragraph introduces the topic of the video, which is chapter 1.7 on modeling with equations, specifically focusing on solving word problems. The instructor emphasizes the importance of reading word problems thoroughly and multiple times to understand the context and identify key information. The summary explains the process of sifting through irrelevant details to find the 'gold' or essential elements of the problem, such as the variables and the relationships between them. The instructor also discusses the general approach to solving word problems, including the use of decimals for answers and the importance of accuracy in the context of the problem.
🎨 Guidelines for Solving Word Problems
The second paragraph outlines a step-by-step approach to solving word problems. It begins with reading the problem multiple times to grasp the details and make notes. The instructor suggests drawing a picture to visualize the problem and then verifying the picture against the problem statement. Identifying the variable, usually indicated in the last sentence, is crucial. The paragraph also covers labeling the picture in terms of the variable, creating expressions and equations using relevant information, and ensuring the solution answers the actual question posed. The instructor highlights the need to apply the value of the variable to the situation to find the final answer.
🔢 Common Equations in Application Problems
This paragraph provides an overview of common equations that are frequently used in solving application problems at the algebra level. Examples include simple interest calculations with the formula i = prt, mixture problems with concentration formulas, distance problems using d = rt, area and perimeter calculations for different shapes, and rate of work problems. The instructor explains each formula and how the variables are represented, providing a foundation for understanding how to translate word problems into mathematical equations.
🚴♂️ Example Problem: Cyclists Riding in Opposite Directions
The fourth paragraph presents a word problem involving two cyclists starting from the same point and riding in opposite directions. One cyclist rides twice as fast as the other, and after three hours, they are 81 miles apart. The instructor demonstrates the problem-solving process by reading the problem, drawing a diagram, labeling the diagram with variables, and setting up an equation to solve for the unknown rates of the cyclists. The solution process involves creating a linear equation based on the given information and solving for the variable representing the slower cyclist's speed, then determining the faster cyclist's speed.
🌿 Example Problem: Creating an Herbal Mixture
In this paragraph, the instructor tackles a mixture problem where the goal is to create a five-pound herbal mixture with an 18% concentration of a particular herb using two existing mixtures, one with 20% concentration and the other with 15%. The process involves reading the problem multiple times, drawing a diagram to represent the mixtures, and setting up an equation based on the concentration formula. The instructor solves the equation to find the amount of each mixture needed, emphasizing the importance of understanding the final answer in the context of the problem.
📉 Conclusion of the Application Problems Section
The final paragraph wraps up the video script by summarizing the process of solving application problems and indicating that the next section will continue the discussion. The instructor reiterates the importance of understanding the problem, using the correct formulas, and applying the solution to answer the actual question posed. This paragraph serves as a conclusion, highlighting the key takeaways from the video and preparing viewers for further learning in subsequent sections.
Mindmap
Keywords
💡Modeling with Equations
💡Word Problems
💡Application Problems
💡Decimal Places
💡Fractions
💡Guidelines for Modeling
💡Variables
💡Relationships
💡Drawing a Picture
💡Keywords
💡Equations
💡Simple Interest
💡Mixtures
💡Distance Problems
💡Area and Perimeter
💡Rate of Work
Highlights
Introduction to Chapter 1.7 on modeling with equations, focusing on solving word problems.
Emphasis on the importance of dealing with word problems and the general dislike among students.
Guidance on using one or two decimal places for answers in word problems, depending on the context.
The strategy of reading a word problem multiple times to understand and solve it effectively.
Highlighting the need to sift through information to find what's important in word problems.
Identifying the variable in a word problem, which is often what the problem is asking for.
The relationship between items in a word problem and how it helps form equations.
The recommendation to draw a picture to visualize and understand the word problem better.
Reading the problem again to ensure the picture and problem align and make sense.
Identifying the variable and labeling the picture in terms of that variable.
Creating expressions and equations using keywords that translate into mathematical symbols.
The necessity of answering the actual question posed by the word problem, not just solving for the variable.
Common equations in application problems, such as simple interest (i = prt).
Explanation of mixture problems, using the formula c = x/v to find the concentration in a mixture.
Approach to distance problems using the formula d = rt, where d is distance, r is rate, and t is time.
Use of area and perimeter formulas for different shapes in word problems.
The rate of work formula a = t/r, where a is the amount of job completed, t is time, and r is the rate of work.
Solving an example problem involving two cyclists starting from the same point and riding in opposite directions.
Solving a mixture problem involving creating a herbal mixture with a specific concentration.
Conclusion and transition to the next section, Section 1.8.
Transcripts
Browse More Related Video
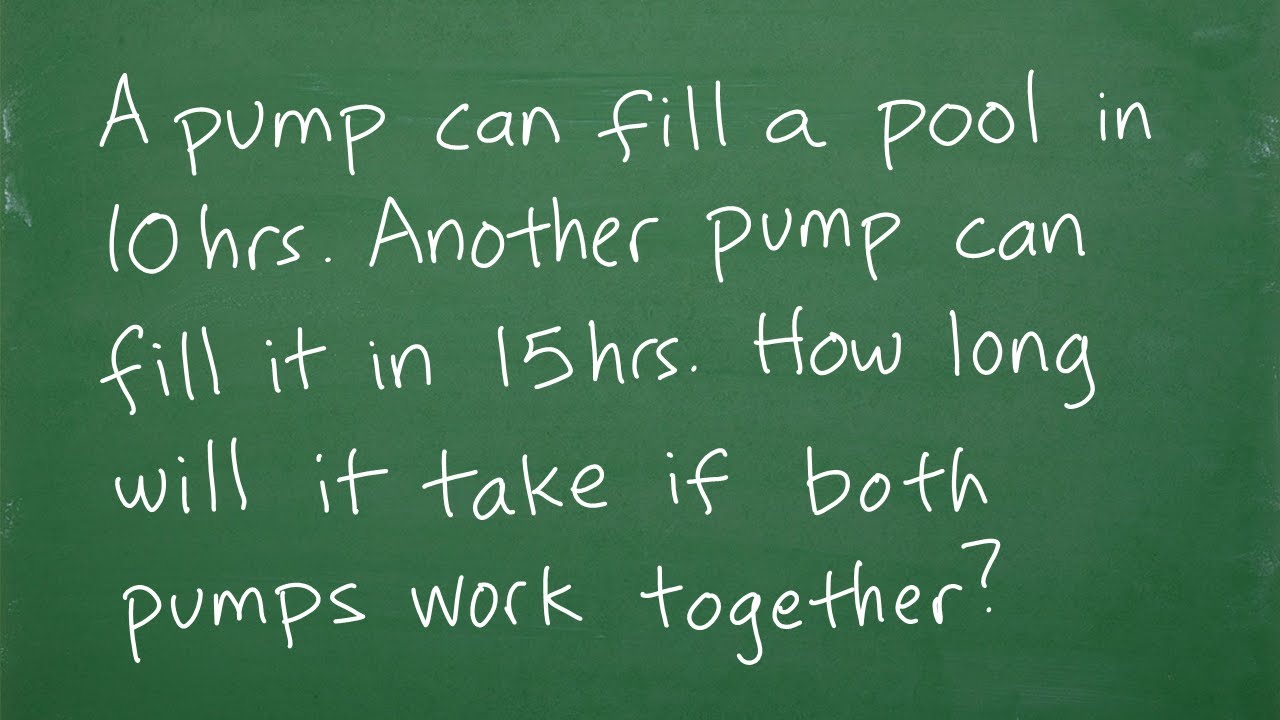
A pump can fill a pool in 10hrs. Another pump can fill it in 15hrs. Both pumps together will take?

Algebra SYSTEM WORD PROBLEM – Let’s solve it step-by-step...

How To Solve Word Problems of Any Kind . Nutshell maths-2

Lesson 1 - Real Numbers And Their Graphs (Algebra 1 Tutor)

Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra

College Physics 1: Lecture 10 - Solving 1-D Motion Problems
5.0 / 5 (0 votes)
Thanks for rating: