Solving problems for acceleration
TLDRThe video script provides a comprehensive review of the fundamental concepts of velocity and acceleration, with a focus on their practical application through various problems. It begins with a straightforward calculation of average velocity for a student running 250 meters in 30 seconds. The second problem delves into acceleration, illustrating how to calculate it by finding the change in velocity over time for a student running different distances. The third problem offers multiple methods to determine the speed of a plane traveling 400 kilometers in 30 minutes, showcasing the flexibility in unit conversion and calculation. Finally, the script tackles the calculation of acceleration for a car starting from rest and reaching a velocity of 54 km/h in 5 seconds, emphasizing the importance of unit conversion and the basic formula for acceleration. The video serves as an educational tool, enhancing understanding of these physics concepts through clear examples and step-by-step solutions.
Takeaways
- 📐 The concept of velocity is introduced as the rate of change of distance over time, which is calculated as distance divided by time.
- 🏃♀️ A student's average speed during a track practice is determined by dividing the distance covered (250 m) by the time taken (30 seconds), resulting in 8.33 m/second.
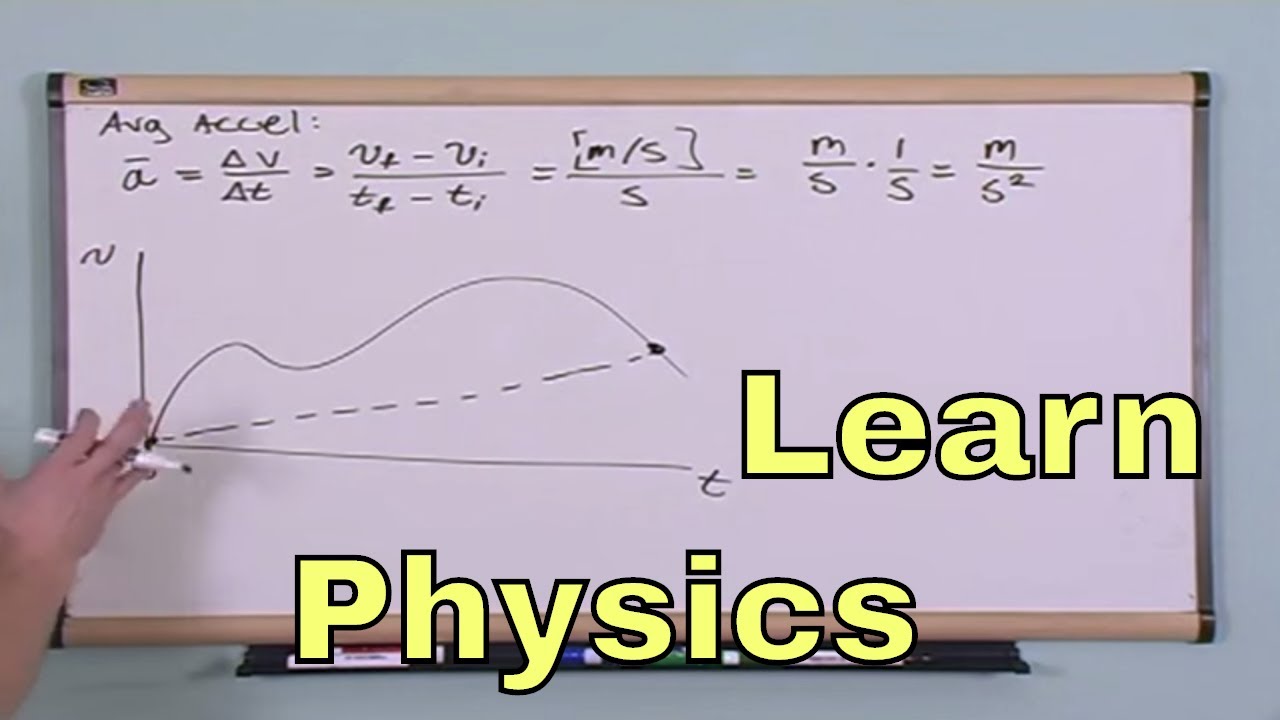
- 🚀 Acceleration is defined as the change in velocity over time, which requires calculating initial and final velocities to find the acceleration.
- ⏱️ To find velocities, the script uses the formula of distance divided by time, which is applied to both the initial and final states of motion.
- 🔢 The script demonstrates how to convert units from kilometers per hour to meters per second for accurate calculations of velocity and acceleration.
- 📉 The initial velocity for the running student is calculated as 6.67 m/s when she covers 200 m in 30 seconds.
- 📈 The final velocity for the running student is calculated as 10 m/s when she covers 300 m in 30 seconds.
- 📊 By applying the acceleration formula, the student's acceleration during the track meet is found to be 0.11 m/s².
- ✈️ A plane's velocity is calculated by dividing the distance traveled (400 km) by the time (0.5 hours), resulting in 800 km/h or 13.33 km/min.
- 🚗 A car's acceleration is calculated by converting the final velocity from km/h to m/s and dividing the change in velocity by the time taken, yielding 3 m/s².
- 🔄 The script emphasizes the importance of unit conversion for consistent and accurate physical calculations, especially when dealing with different units of time and distance.
- 📋 The video serves as an educational tool for understanding and solving problems related to velocity and acceleration using their respective equations.
Q & A
What is the average velocity of the student who ran 250 meters in 30 seconds?
-The average velocity is calculated using the formula distance over time. Plugging in the values, 250 meters over 30 seconds, results in an average velocity of 8.33 meters per second.
What is the formula for calculating acceleration?
-Acceleration is calculated using the formula final velocity minus initial velocity, all over time (a = (v_f - v_i) / t).
How do you find the final and initial velocities for the student running in the track meet?
-You find the final and initial velocities by using the formula velocity equals distance over time. For the final velocity, use 300 meters over 30 seconds to get 10 m/s, and for the initial velocity, use 200 meters over 30 seconds to get 6.67 m/s.
What is the acceleration of the student who ran 200 meters and then 300 meters in 30 seconds each?
-To find the acceleration, you use the final velocity (10 m/s), the initial velocity (6.67 m/s), and the time (30 seconds). The acceleration is calculated as (10 m/s - 6.67 m/s) / 30 s, which equals 0.1 m/s².
How can you determine the velocity of a plane that traveled 400 km in 30 minutes?
-You can convert the time to hours (0.5 hours) and then divide the distance (400 km) by the time to get the velocity in km/h. Alternatively, you can calculate the velocity in kilometers per minute by dividing 400 km by 30 minutes.
What are the two different ways to calculate the plane's velocity in the script?
-The first way is to divide 400 km by 0.5 hours to get 800 km/h. The second way is to calculate the velocity per minute by dividing 400 km by 30 minutes, resulting in 13.33 km/min.
What is the acceleration of a driver who starts from a parked car and reaches a velocity of 54 km/h within 5 seconds?
-First, convert the velocity from km/h to m/s by dividing 54 km by 3600 seconds and multiplying by 1000 meters. This gives 15 m/s. Then, use the acceleration formula with a final velocity of 15 m/s, an initial velocity of 0 m/s, and a time of 5 seconds to get an acceleration of 3 m/s².
Why is it necessary to convert units when calculating acceleration in the script?
-Unit conversion is necessary to ensure that all measurements are in the same unit system, which allows for accurate calculations. For instance, converting km/h to m/s is required to calculate acceleration in meters per second squared.
How does the script demonstrate the application of the velocity and acceleration equations in real-world scenarios?
-The script uses examples such as a student practicing for a track meet, a plane's flight, and a car's acceleration to illustrate how the equations for velocity and acceleration can be applied to solve practical problems involving motion.
What is the significance of understanding the difference between speed and velocity?
-Speed is a scalar quantity that refers to how fast an object is moving, while velocity is a vector quantity that includes both the speed and direction of the object's motion. Understanding this difference is crucial for accurately describing and calculating motion.
Why is it important to consider the initial and final velocities when calculating acceleration?
-Acceleration is the rate of change of velocity over time. Knowing the initial and final velocities allows you to determine how much the velocity has changed and in what direction, which is essential for calculating the acceleration.
How can one use the information provided in the script to solve problems involving different units of time and distance?
-The script provides methods for converting between different units of time (seconds, minutes, hours) and distance (meters, kilometers). By applying these conversions, one can solve problems involving various units and ensure that the units are consistent when using the equations for velocity and acceleration.
Outlines
🏃♂️ Understanding Velocity and Acceleration Concepts
This paragraph introduces the concepts of velocity and acceleration, and their application in solving physics problems. It covers the calculation of average speed using the rate equation (distance over time), where a student's velocity is determined after running 250 meters in 30 seconds, resulting in an average velocity of 8.33 m/second. The paragraph also delves into a more complex scenario involving acceleration, where a student's change in velocity over time is calculated after running different distances in equal time frames. The velocities at various points are determined by dividing the distance by the time taken, leading to the calculation of acceleration as the change in velocity over time. The paragraph concludes with a problem involving a plane's velocity, solved by converting units from kilometers to meters and minutes to hours, and a car's acceleration calculated from rest to a certain velocity over a short time span.
📐 Solving for Acceleration with Unit Conversion
The second paragraph focuses on solving problems related to acceleration, emphasizing the importance of unit conversion. It starts with a problem where a driver accelerates a car from rest to a velocity of 54 km/h in 5 seconds. To solve this, the velocity is first converted from km/h to m/s by considering the number of meters in a kilometer and the number of seconds in an hour. With the final velocity at 15 m/s and the initial velocity at zero (since the car was at rest), the acceleration is calculated by dividing the change in velocity by the time taken, resulting in an acceleration of 3 m/s². This paragraph highlights the methodical approach to solving physics problems by breaking down the steps and ensuring unit consistency throughout the calculations.
Mindmap
Keywords
💡Velocity
💡Acceleration
💡Speed
💡Rate Equation
💡Initial Velocity
💡Final Velocity
💡Distance
💡Time
💡Units Conversion
💡Average Speed
💡Direction
💡Scalar and Vector Quantities
Highlights
The video reviews the fundamental concepts of velocity and acceleration, and their application through equations.
Velocity and speed are essentially the same in this context, and the rate equation is distance over time.
A student's average speed during a track practice is calculated as 8.33 m/second over a distance of 250 meters in 30 seconds.
Acceleration is defined as the change in velocity over time, which requires calculating initial and final velocities first.
The runner's final velocity is determined by dividing the distance covered (300m) by the time taken (30 seconds), resulting in 10 m/s.
The initial velocity is calculated similarly, yielding 6.67 m/s for the first 200 meters covered in 30 seconds.
By using the initial and final velocities, the runner's acceleration is found to be a positive 0.11 m/s² over 30 seconds.
The velocity equation Δv = vₑ - v₀ / t can be used to solve for a plane's speed, given its distance and time.
Two methods are presented for calculating the plane's speed: one using kilometers per hour and another using kilometers per minute.
Both methods yield correct answers, demonstrating the flexibility of units in solving physics problems.
A driver's acceleration is calculated from a stationary start to a velocity of 54 km/h over 5 seconds.
Unit conversion is necessary to express the driver's velocity in meters per second (15 m/s from 54 km/h).
The acceleration is calculated by subtracting the initial velocity (zero) from the final velocity (15 m/s) and dividing by time (5 seconds).
The final answer for the driver's acceleration is 3 m/s², illustrating the application of the acceleration formula.
The video provides a comprehensive understanding of how to use velocity and acceleration equations to solve practical problems.
The importance of unit conversion in physics problems is emphasized for accurate calculations.
The video demonstrates the step-by-step process of solving for velocity and acceleration, making complex concepts more accessible.
Practical examples are used to illustrate the application of physics concepts, enhancing the viewer's ability to understand and apply these principles.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: