4.3 Calculating Work with Angles
TLDRIn this educational video, Mr. Dyson delves into the concept of work in physics, focusing on scenarios where force is applied at an angle. He starts by recapping the basic definition of work—force causing movement—and then explores the complexities introduced when the force vector and direction of movement are not aligned. Through practical examples involving a box on a floor and various other objects, Mr. Dyson illustrates how to calculate the component of the force that contributes to work using the cosine of the angle between the force and the movement direction. The video emphasizes the real-world application of these principles, enhancing understanding of how forces affect motion and work in different contexts.
Takeaways
- 📐 The definition of work in physics involves a force applied to an object in the direction of its movement, resulting in the object's displacement.
- ⚙️ When force is applied at an angle to the displacement, only the component of the force in the direction of movement contributes to the work done.
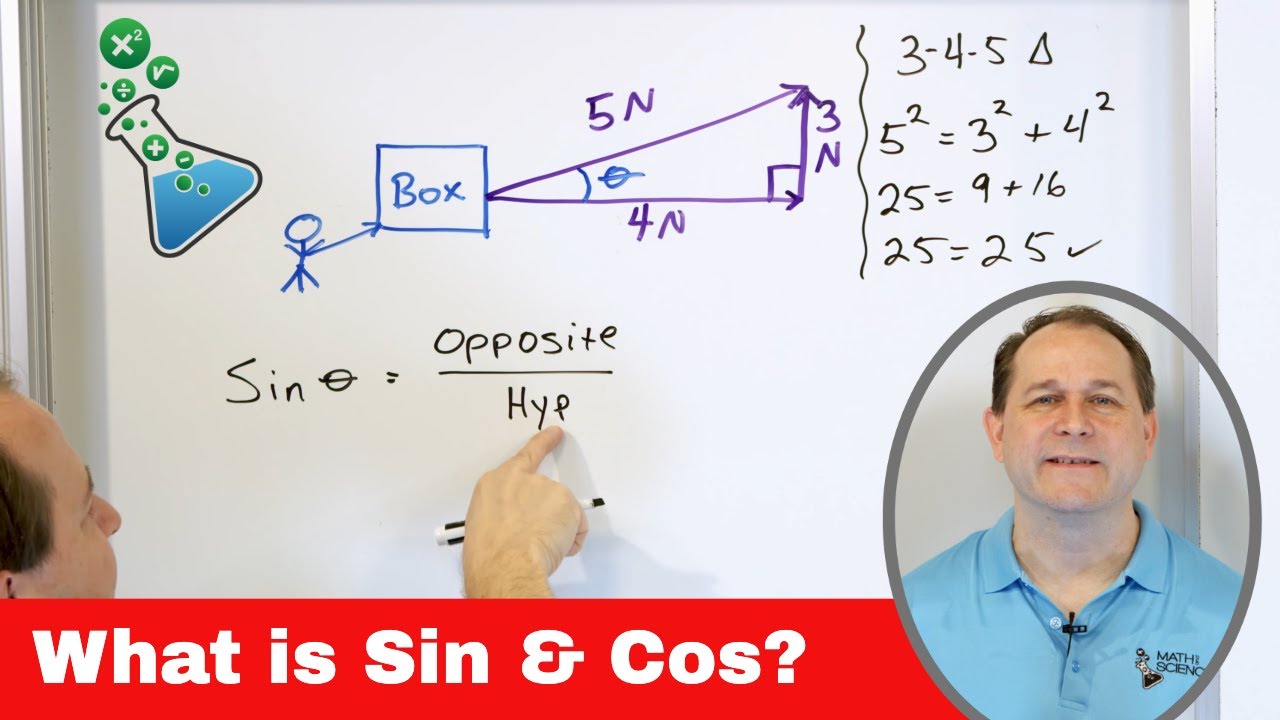
- 📈 The formula to calculate work done at an angle (θ) is Work = F * D * cos(θ), where F is the force, D is the displacement, and θ is the angle between the force and the displacement.
- 🧮 Work done by a force is considered positive if it aids in the object's movement and negative if it opposes the movement, such as friction.
- 📉 The net work done on an object is the sum of all the individual works by different forces acting on the object, considering their directions.
- 🔄 The net force acting on an object results in a change in the object's energy and velocity, indicating that work is being done.
- 🌟 An example given is a box being pulled by a rope at an angle, where the work done is calculated using the formula Work = F * D * cos(θ).
- 🚫 When an object moves at a constant velocity, such as an ice skater gliding without an applied force, the net work done is zero because there is no net force causing displacement.
- 🔢 The concept of net work is applied by summing the work done by all forces acting on an object, including those that may be opposing the motion.
- ⚖️ The net force can be calculated using the formula Net Force = F * cos(θ), and this net force is used to determine the net work done on an object.
- 🚀 In scenarios involving acceleration, such as a pickle being accelerated across a floor, the net work done is calculated using the net force (resulting from all forces, including friction) multiplied by the distance moved.
Q & A
What is the definition of work in the context of physics?
-In physics, work is defined as the product of the force applied to an object and the distance the object moves in the direction of the force.
When is work done considered positive and when is it negative?
-Work is considered positive when the force causes the object to move in the direction of the force, and negative when the force acts against the direction of motion.
How do you calculate the work done by a force that is applied at an angle to the displacement?
-To calculate the work done by a force applied at an angle, you use the formula: work = F * D * cos(theta), where F is the magnitude of the force, D is the distance moved by the object, and theta is the angle between the force and the direction of displacement.
What is the role of the normal force when a box is pushed at an angle?
-The normal force acts perpendicular to the surface and supports the weight of the object. It does not contribute to the work done on the box when the box is not moving vertically, as it counteracts gravity.
What is the net work done on an object when multiple forces act on it?
-The net work done on an object is the sum of all the individual works done by each force acting on the object. It is calculated by adding the work done by all forces in the direction of motion and subtracting the work done by forces acting in the opposite direction.
Why is the net work done on an object at rest or moving at a constant velocity zero?
-The net work done is zero when an object is at rest or moving at a constant velocity because there is no net force acting on the object (all forces are balanced), and therefore, no change in kinetic energy.
How do you calculate the work done by friction?
-The work done by friction is calculated by multiplying the frictional force by the distance over which the object moves. If the friction force is opposite to the direction of motion, the work done is negative.
What is the relationship between net force, work, and the acceleration of an object?
-The net force acting on an object is equal to the mass of the object times its acceleration (F = m * a). The net work done on the object is equal to the net force times the distance the object moves in the direction of the net force.
In the example of the ice skater, why is the net work done considered zero?
-For the ice skater moving at a constant velocity, the net work done is zero because there is no net force acting on the skater (the forward force is balanced by frictional forces), resulting in no change in kinetic energy.
How does the mass of an object affect the net work done on it?
-The mass of an object affects the net work done on it through its influence on the net force, as per Newton's second law (F = m * a). A greater mass requires a greater net force to achieve the same acceleration, and thus, to do the same amount of work over a given distance.
Can you provide an example of how to calculate the net work done on an object using the given formula?
-Certainly. Consider an object being pulled with a force of 75 N over a distance of 10 m at an angle of 20 degrees with the horizontal, and a frictional force of 30 N acting opposite to the direction of motion. The work done by the pulling force is F * D * cos(theta) = 75 N * 10 m * cos(20°) = 705 J. The work done by friction is frictional force * distance = -30 N * 10 m = -300 J. The net work done on the object is the sum of these works: 705 J - 300 J = 405 J.
Outlines
🔍 Understanding Work by Force at an Angle
This paragraph introduces the concept of calculating work done when a force is applied at an angle to the displacement of an object. It emphasizes that work is only done by the component of the force in the direction of the object's movement. The paragraph uses the example of a box being pushed at an angle to illustrate how to calculate the work done by considering the angle between the force and the direction of motion, using the formula work = force * distance * cos(theta), where theta is the angle between the force and the x-axis.
📐 Calculating Work with Examples
The second paragraph delves into examples to demonstrate the calculation of work done on objects when a force is applied at an angle. It covers three scenarios: a box of petunias being dragged by a rope at an angle, an ostrich being pulled into a living room, and a force applied to an object at an angle to find the distance moved. Each example uses the work formula, emphasizing that only the component of the force in the direction of movement contributes to the work done. The paragraph also introduces the concept of net work, which is the sum of all the work done by individual forces acting on an object.
🚫 Friction and Net Work Calculation
This paragraph discusses the calculation of net work, which is the total work done on an object when multiple forces are acting upon it, such as an applied force and friction. It explains that the net work is the sum of the work done by each force, considering their directions as positive or negative. Examples include a person pushing a box with friction present and an ice skater gliding across the ice. The paragraph clarifies that if there is no force causing movement, as in the case of the ice skater, no work is done, resulting in zero net work.
🏋️ Force and Work in Acceleration and Motion
The final paragraph explores the net work done on an object being accelerated, using the example of a 25 kg pickle being accelerated across a floor. It connects the concept of work to the principles of kinematics, using the formula for acceleration to find the net force acting on the pickle. The paragraph demonstrates how to calculate the net work done on the object by multiplying the net force by the distance over which it acts, taking into account the friction force as part of the net force.
Mindmap
Keywords
💡Work
💡Force
💡Displacement
💡Angle of Force
💡Cosine of Angle
💡Net Work
💡Friction Force
💡Normal Force
💡Tension Force
💡Newton's Laws
💡Joules
Highlights
Work is defined as force applied to an object in the direction of its movement.
When force and displacement are at an angle, only the component of the force in the direction of displacement contributes to work done.
The formula for work done when force is applied at an angle (theta) is Work = F * D * cos(theta).
The angle (theta) is between the force and the direction of motion, not necessarily the horizontal.
In the example of a box being dragged, the work done by the tension force is calculated considering the angle of the rope.
The weight of the box (55 Newtons) and normal force do not contribute to work as there is no vertical movement.
The net work done on an object is the sum of the work done by each individual force, considering their direction.
Friction always does negative work as it opposes the direction of motion.
Total work is the algebraic sum of the work done by all forces acting on an object.
When calculating net work, it's essential to consider the direction of each force and its contribution to the object's movement.
In the case of an ice skater gliding at a constant velocity, the net work done is zero because there is no net force acting on the skater.
For an object moving under the influence of multiple forces, the net work is calculated by summing the work done by the applied force and subtracting the work done by friction.
When an object is accelerating, the net force can be determined using Newton's second law (F = m * a), which is then used to calculate net work.
The friction force's contribution to work is implicitly included in the net force calculation, so it does not need to be calculated separately.
In physics problems involving work, it's crucial to identify the forces doing work and the forces not contributing to work due to their direction.
The cosine function is used to find the horizontal component of a force when calculating work in scenarios involving angles.
Understanding the concept of net work is fundamental to analyzing the total energy transfer in a system with multiple forces.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: