Calculus Complete the Square and Integrate
TLDRThe video script discusses the technique of completing the square and its application in integration, a method often encountered in calculus and AP exams. The presenter outlines situations where completing the square is beneficial, such as when u-substitution is not immediately viable or when the integral resembles an inverse trigonometric function. Three examples are provided to illustrate the process: integrating a rational function with a quadratic in the denominator, a radical with a quadratic expression, and a more complex integral resembling arctan. The presenter emphasizes a common shortcut used in AP exams and demonstrates how to transform the integral into a recognizable form, such as arcsine or arctan, before integrating. The script serves as a helpful guide for students to tackle complex integrals using completing the square as a preliminary step.
Takeaways
- 📚 Completing the square is a technique often used in calculus when u-substitution or natural log methods don't immediately work out.
- 🔍 The first step is to identify if the integral resembles an inverse trigonometric function or has a quadratic in the denominator, which are common scenarios for using this technique.
- ✅ An example given is the integral of dx over (x^2 + 6x + 10), which is almost a perfect square, and can be manipulated into a recognizable form for integration.
- 🔢 To complete the square, you may need to add and subtract the same value to create a perfect square trinomial, and then simplify the expression.
- 📐 Recognizing patterns such as (x + a)^2 can help simplify the integral and lead to a common integral form like arctan(x + a).
- 🧩 For more complex integrals, like one with a square root of a quadratic in the denominator, factoring and rearranging terms can help create a perfect square trinomial.
- ➗ Factoring out a negative or other constants can simplify the expression and make it easier to integrate, as demonstrated in the script.
- 🔁 Rearranging terms can sometimes make the integral resemble a known form, such as arcsine, which can be integrated directly.
- 💡 In cases where the integral does not perfectly match a known form, factoring out constants or making a u-substitution can lead to a recognizable integral form.
- 📉 The process of completing the square can involve breaking down the quadratic term, adding and subtracting terms to create a perfect square, and then integrating the simplified form.
- ⛓️ The technique is particularly useful for AP calculus problems and can be a shortcut for solving more complex integrals.
- ✨ Practice and familiarity with completing the square and recognizing patterns can greatly simplify the process of integrating more complex functions.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the technique of completing the square and then integrating, which is often used in calculus.
When might one consider using the completing the square technique for integration?
-One might consider using the completing the square technique when u-substitution doesn't work out immediately, the integral looks like a natural log but is a bit off, or it resembles an inverse trigonometric function.
What is an example of a problem where completing the square is used?
-An example given is the integral of dx over (x^2 + 6x + 10), where x^2 + 6x is almost a perfect square, and the technique helps simplify the integral.
How does the video demonstrate completing the square on the trinomial x^2 + 6x + 10?
-The video demonstrates it by adding and subtracting 9 (to make a perfect square) and then dividing 10 into +9 and +1 to maintain the equality, resulting in the expression 1 + (x + 3)^2.
What is the integral of dx over the square root of a quadratic expression, and how is it approached?
-The integral is approached by factoring out a negative sign and completing the square within the quadratic. The video demonstrates this by rearranging terms and using the perfect square trinomial to simplify the integral.
How does the video handle the more complicated integral with x^2 + 4x in the denominator?
-The video suggests breaking up the coefficient of x (which is 4) into two parts (+4 and +4), completing the square with x + 2, and then rewriting the expression to make it resemble an arctan function.
What substitution is made to rewrite the integral in terms of U?
-The substitution made is U = (x + 2) / 2, and then the integral is rewritten in terms of U with 2dU = dx.
What is the final form of the integral after completing the square and substitution in the more complicated example?
-The final form of the integral is (1/2) * arctan(U) + C, where U = (x + 2) / 2.
Why is the completing the square technique particularly useful for AP calculus problems?
-The completing the square technique is particularly useful for AP calculus problems because it often works as a shortcut for problems that frequently appear on the AP exam.
What is the general approach when an integral resembles an inverse trigonometric function but is not quite perfect?
-The general approach is to complete the square on the trinomial, factor out constants, and then use a substitution to rewrite the integral in a form that resembles an inverse trigonometric function.
How does the video script help in understanding the process of completing the square and integrating?
-The video script provides step-by-step examples with detailed explanations, showing how to recognize when to use the technique, how to perform the necessary algebraic manipulations, and how to simplify the integral into a recognizable form that can be easily integrated.
What is the significance of recognizing a perfect square trinomial when integrating?
-Recognizing a perfect square trinomial allows for the simplification of the integral into a form that can be easily integrated, often resulting in an inverse trigonometric function, which is a common outcome in calculus problems.
Outlines
📚 Completing the Square and Integration Techniques
This paragraph introduces the topic of completing the square and integration, which are techniques that might be necessary to solve certain calculus problems. The speaker discusses common scenarios where these methods are used, such as when u-substitution or natural log methods do not immediately work. The paragraph provides an example of integrating DX over x squared plus 6x plus 10, demonstrating how to recognize and complete the square in a trinomial expression and then integrate it, resulting in an arctan function plus a constant C.
🔍 Advanced Integration with Completing the Square
The second paragraph delves into more complex integration problems that involve completing the square. The speaker begins by addressing an integral with a quadratic in the denominator, which initially appears messy. By factoring out a negative and rearranging terms, the speaker forms a perfect square trinomial, which simplifies the integral to the form of an arcsine function. The paragraph continues with a more complicated example, where the speaker breaks down the steps to complete the square on a trinomial and then integrates it. The process involves factoring out constants and using substitution to transform the integral into a recognizable form, such as arctan, which can be integrated to find the antiderivative. The speaker emphasizes that these techniques are commonly encountered in AP calculus exams and are generally useful in solving a variety of calculus problems.
Mindmap
Keywords
💡Completing the Square
💡Integrating
💡u-Substitution
💡Natural Log
💡Inverse Trig Function
💡Quadratic
💡AP Exam
💡Arctan
💡Arcsine
💡Factoring
💡Differential
Highlights
The video discusses completing the square and integrating, a technique that might be necessary in certain calculus problems.
Completing the square is useful when u-substitution doesn't work out immediately or when the integral resembles an inverse trigonometric function.
The first example involves integrating DX over x^2 + 6x + 10, which is a case where completing the square is effective.
The trinomial x^2 + 6x is almost a perfect square, and the video demonstrates how to modify the expression to complete the square.
Completing the square involves rewriting the trinomial as (x + 3)^2 + 1, which simplifies the integration process.
The integral can be recognized as an arctan function after completing the square, leading to a solution of arctan(x + 3) + C.
The second example shows integrating over the square root of a quadratic, which initially appears messy.
By factoring out a negative and rearranging terms, the video demonstrates how to prepare the expression for completing the square.
The resulting expression after completing the square resembles an arcsine function, leading to the integral of arcsin(x + 5) + C.
The third example is more complex, involving a closer look at the structure of the trinomial before completing the square.
The video shows an alternative approach by breaking down the constant term 8 into 4 + 4, although it's not necessary for solving the problem.
Factoring out a 4 from the denominator simplifies the expression and makes it resemble an arctan function.
The integral is then transformed into terms of U, where U = (x + 2)/2, allowing for an easier integration using arctan.
The final integral solution is expressed in terms of U and then converted back to x, resulting in arctan((x + 2)/2) + C.
Completing the square is a common technique used in calculus, particularly on AP exams, and this video provides a shortcut method for solving such problems.
The video emphasizes that while there are alternative ways to approach these problems, the demonstrated technique works effectively for most AP exam problems.
The presenter provides a step-by-step guide, making the complex process of completing the square and integrating more accessible.
The video concludes by wishing viewers good luck, emphasizing the practical application of these techniques in calculus and AP exams.
Transcripts
Browse More Related Video

Integration using completing the square and the derivative of arctan(x) | Khan Academy

U-Substitution 5-sample video

Proving the Quadratic Formula - Twice (Precalculus - College Algebra 20)

Integration of Rational Functions By Completing The Square - Calculus
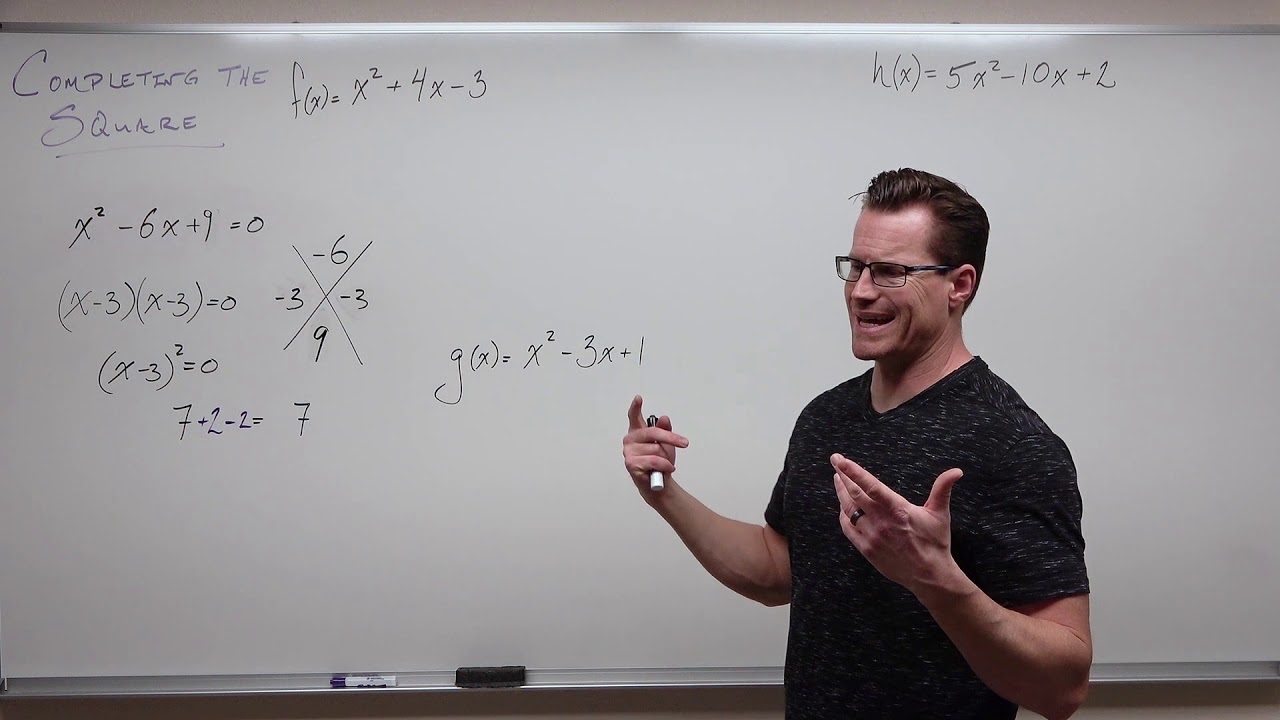
Completing the Square Made Easy (Precalculus - College Algebra 19)

_-substitution: defining _ | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: