Add, Subtract, Multiply, Divide Imaginary & Complex Numbers - [1]
TLDRThe video script offers an insightful exploration into the realm of complex numbers, a fundamental concept for students venturing into calculus. The instructor emphasizes the importance of understanding algebra as a prerequisite and addresses the common misconceptions surrounding complex numbers, often mistakenly considered as 'imaginary' or non-existent. The script delves into solving equations involving square roots of negative numbers, illustrating the solution process with examples like x^2 = -25, which leads to the introduction of the imaginary unit 'i', defined as the square root of -1. The video also covers the arithmetic of complex numbers, including addition, multiplication, and dealing with complex numbers in denominators through the use of complex conjugates. The instructor provides a step-by-step guide on simplifying complex expressions and highlights the ubiquity and utility of imaginary numbers in higher mathematics, particularly calculus. The summary concludes with solving a quadratic equation with a negative discriminant, showcasing how complex numbers provide solutions where real numbers fail, thus reinforcing their practical significance in mathematical problem-solving.
Takeaways
- 📚 The course aims to prepare students for calculus by covering the gap in knowledge between algebra and calculus, often taught in pre-calculus or trigonometry.
- 🔍 Complex numbers, despite their name, are essential for understanding higher levels of mathematics and are not as daunting as they seem.
- 🤔 The concept of imaginary numbers, denoted by 'i', is introduced as a solution to equations involving the square root of negative numbers, where i is defined as the square root of -1.
- 🧮 When taking the square root of a negative number, you take the square root of the absolute value and append 'i' to indicate the imaginary component.
- 🤓 There are two types of solutions for equations with negative square roots: positive 'ni' and negative 'ni', where 'n' is the absolute value of the number under the square root.
- 📐 The number line is expanded in complex number theory to include an imaginary axis perpendicular to the real axis, allowing for two-dimensional representation of complex numbers.
- 📈 Real numbers are a subset of complex numbers, where the imaginary part is zero, and every complex number can be expressed in the form a + bi, where 'a' is the real part and 'b' is the imaginary part.
- 🤝 Addition of complex numbers is performed by adding the real parts together and the imaginary parts together, maintaining the complex number structure.
- 💡 Multiplication of complex numbers is similar to polynomial multiplication, using the FOIL method, with the crucial understanding that i^2 = -1.
- 🛑 When a complex number is in the denominator, it is simplified by multiplying both the numerator and denominator by the complex conjugate of the denominator.
- ✅ The complex conjugate of a complex number a + bi is a - bi, and it is used to eliminate the imaginary part from the denominator when simplifying fractions.
- 🔑 Imaginary and complex numbers are not only fundamental in mathematics but also have practical applications in fields like engineering, physics, and even in financial models.
Q & A
What is the main goal of the course mentioned in the transcript?
-The main goal of the course is to teach students everything they need to know to be prepared for calculus, covering the gap in knowledge that typically occurs between algebra and calculus.
What are complex numbers?
-Complex numbers are numbers that consist of a real part and an imaginary part, often written in the form a + bi, where 'a' is the real part, 'b' is the imaginary part, and 'i' is the imaginary unit.
Why do we use the term 'imaginary numbers'?
-Imaginary numbers are used to represent the square root of a negative number, which cannot be represented by real numbers. The term 'imaginary' can be misleading as these numbers are very real and useful in mathematics, especially in calculus.
What is the significance of 'i' in mathematics?
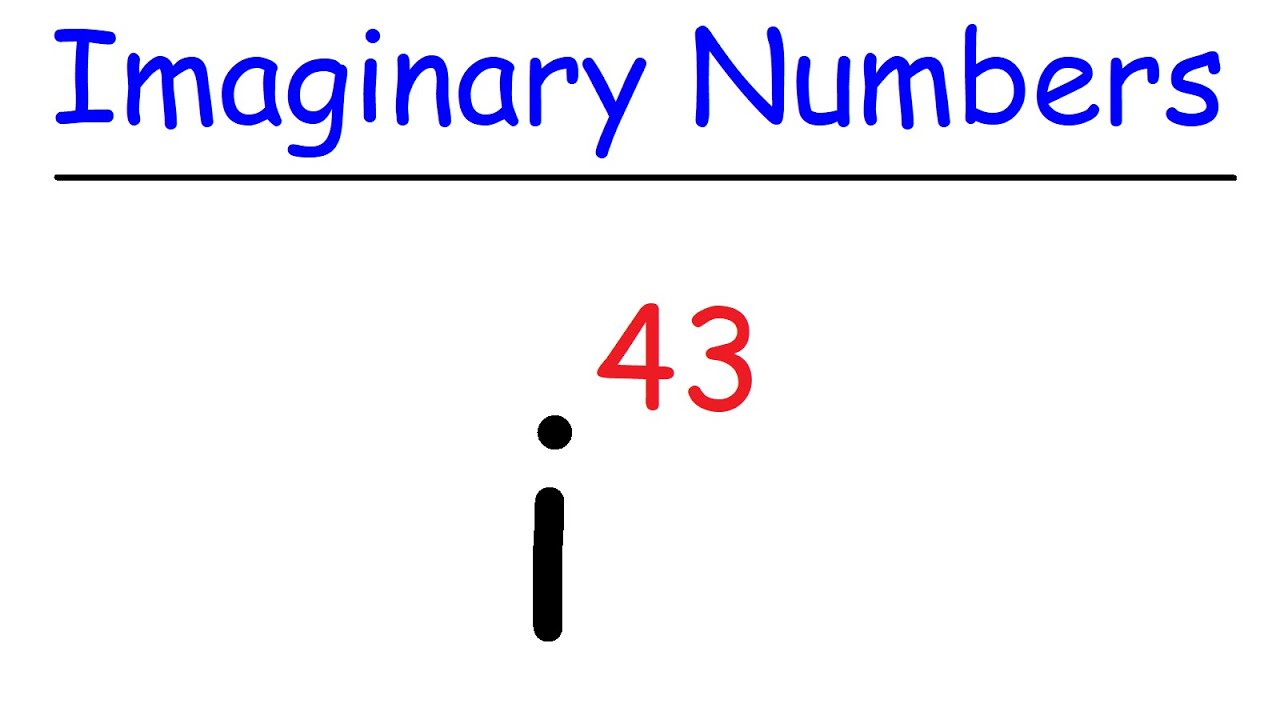
-The letter 'i' is defined as the square root of negative one (i.e., i = √(-1)). It is a fundamental concept in complex number theory and is used to solve equations that involve square roots of negative numbers.
How do you solve the equation x^2 = -25?
-The equation x^2 = -25 is solved by taking the square root of both sides, yielding x = ±√25 * i, which simplifies to x = ±5i. This means there are two solutions: 5i and -5i.
What is the general form of a complex number?
-The general form of a complex number is a + bi, where 'a' is a real number, 'b' is a real number, and 'i' is the imaginary unit.
How do you add two complex numbers?
-To add two complex numbers, you add the real parts together and the imaginary parts together. For example, if you have (3 + 2i) + (4 - 5i), you would add the real parts (3 + 4) and the imaginary parts (2i - 5i) to get (7 - 3i).
How do you multiply two complex numbers?
-To multiply two complex numbers, you use the FOIL method (First, Outer, Inner, Last), making sure to apply the rule that i^2 = -1. For example, (2 + 3i)(4 - 5i) would be calculated as follows: First 2*4 = 8, Outer 2*(-5i) = -10i, Inner 3i*4 = 12i, Last 3i*(-5i) = -15i^2 = 15, and then combine like terms to get (8 - 10i + 12i + 15) = (23 + 2i).
What is the complex conjugate of a complex number?
-The complex conjugate of a complex number a + bi is a - bi. It is used to eliminate the imaginary part when dividing complex numbers by multiplying the numerator and denominator by the conjugate.
Why are imaginary numbers indispensable in calculus?
-Imaginary numbers are indispensable in calculus because they allow for the solution of equations that have no real solutions, such as those involving the square root of a negative number. They are also fundamental in understanding and working with complex functions and in various areas of mathematics and physics.
How do you simplify a complex fraction?
-To simplify a complex fraction, you multiply the numerator and the denominator by the complex conjugate of the denominator. This process cancels out the imaginary terms in the denominator, leaving you with a fraction that has a real denominator, which can then be further simplified if necessary.
Outlines
📚 Introducing Complex Numbers and Algebra's Gap
The paragraph introduces the goal of the course, which is to prepare students for calculus by covering the gap in knowledge between algebra and calculus. It emphasizes the importance of understanding algebra before moving on to more advanced topics. The instructor also introduces the concept of complex numbers, which are often a source of confusion due to their name but are essential for a complete understanding of mathematics, especially in calculus.
🔍 Understanding Imaginary Numbers and Their Utility
This section delves into the concept of imaginary numbers, explaining their relationship with the square root of negative numbers. The instructor clarifies that the term 'imaginary' does not imply non-existence but rather represents a different type of number system. The explanation includes an example of solving an equation involving the square root of a negative number, showcasing how imaginary numbers provide solutions where real numbers fail.
🌐 The Realm of Numbers: Real, Imaginary, and Complex
The paragraph explains the broader classification of numbers, distinguishing between real numbers, imaginary numbers, and complex numbers. It uses examples to illustrate these categories and emphasizes that complex numbers, which combine real and imaginary parts, represent the most general form of numbers. The concept of the number line is expanded to include an imaginary axis, providing a visual representation of where these numbers lie.
🧮 Operations with Complex Numbers
The focus of this paragraph is on performing arithmetic operations with complex numbers, specifically addition. The process is analogous to combining like terms in algebra, with the key difference being the treatment of the imaginary unit 'i'. The instructor demonstrates how to add complex numbers by separating real and imaginary components and emphasizes that every number known until that point can be considered as a complex number with a zero imaginary part.
🤔 Multiplication and Simplification of Complex Numbers
This section covers the multiplication of complex numbers using the FOIL method, similar to polynomial multiplication. The importance of remembering that 'i' squared equals negative one is highlighted to ensure accurate results. The process is demonstrated through an example, showing how to combine like terms and handle the imaginary unit appropriately.
🎓 Simplifying Complex Fractions and Equations
The paragraph discusses the simplification of complex numbers within a fraction by multiplying the numerator and denominator by the complex conjugate. The complex conjugate is defined, and its role in eliminating imaginary numbers from the denominator is explained. The process is illustrated through an example, emphasizing the importance of careful calculation to avoid errors. The section concludes with an example of solving a quadratic equation that results in complex solutions.
🛠️ Solving Quadratic Equations with Complex Solutions
This final paragraph demonstrates how to solve a quadratic equation when the discriminant (b squared minus 4ac) is negative, resulting in complex solutions. The quadratic formula is applied, and the process of taking the square root of a negative number is shown, leading to the conclusion that the solutions involve both real and imaginary parts. The importance of being comfortable with imaginary numbers for solving such equations is stressed.
Mindmap
Keywords
💡Complex Numbers
💡Imaginary Numbers
💡Real Numbers
💡Algebra
💡Calculus
💡Square Root
💡Complex Conjugate
💡Foil Method
💡Quadratic Equation
💡Discriminant
💡Number Line
Highlights
The course aims to prepare students for calculus by covering the gap in knowledge between algebra and calculus.
Complex numbers, often misunderstood due to their name, are introduced as a fundamental concept in the course.
The concept of imaginary numbers is explained, emphasizing their practical use despite the misleading name.
The solution to equations like x^2 = -25 is demonstrated, introducing the imaginary unit 'i'.
The definition of 'i' as the square root of -1 is established as a key concept in understanding complex numbers.
The multiplication of complex numbers is taught using the FOIL method, a technique from algebra.
The importance of imaginary numbers in calculus and higher mathematics is emphasized.
The real, imaginary, and complex numbers are differentiated, with examples provided for each.
The concept of the complex plane, consisting of real and imaginary axes, is introduced.
Addition of complex numbers is demonstrated, showing how to combine like terms.
Multiplication of complex numbers results in another complex number, highlighting the algebraic manipulation involved.
The necessity of avoiding square roots in denominators when simplifying complex numbers is discussed.
The use of the complex conjugate to simplify complex fractions is explained.
The process of simplifying complex numbers in a fraction is demonstrated step by step.
The application of the quadratic formula to solve equations with complex solutions is shown.
The handling of square roots of negative numbers using imaginary units is covered.
The final complex solutions to a quadratic equation are expressed in the form of a + bi.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: