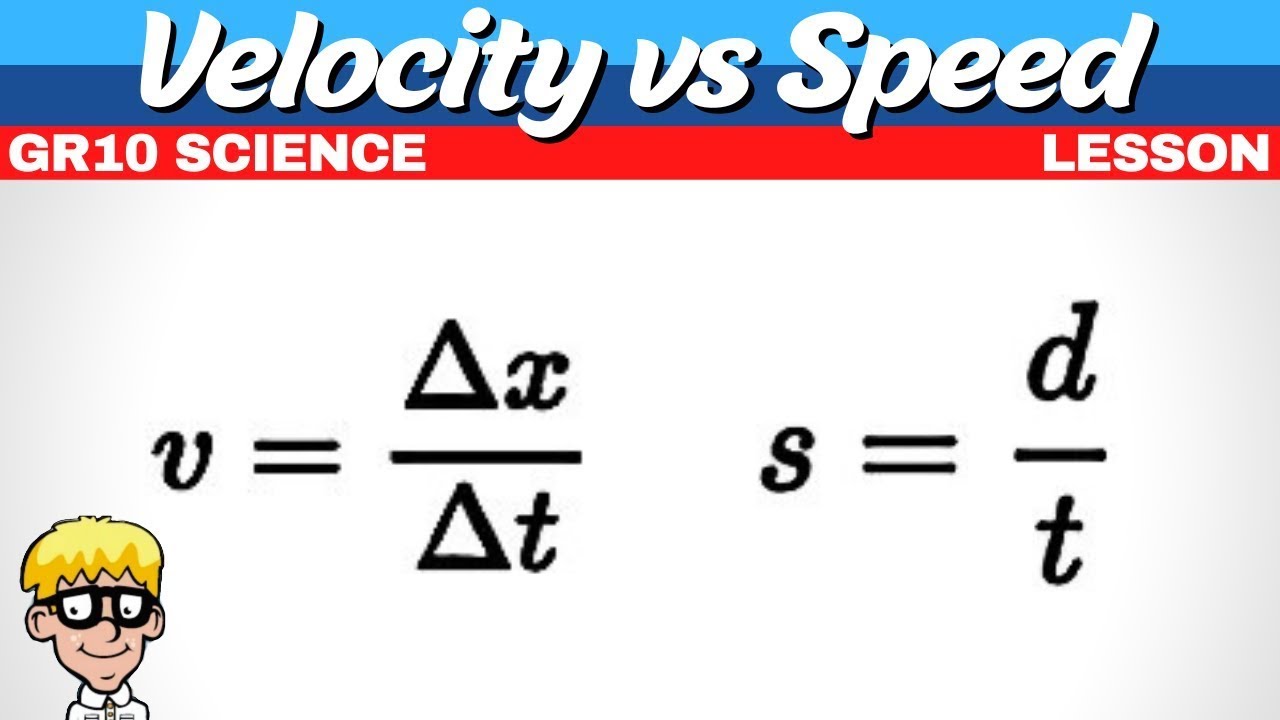GCSE Physics - The difference between Speed and Velocity & Distance and Displacement #51
TLDRThe video script provides a clear distinction between speed and velocity, two fundamental concepts in physics. Speed, a scalar quantity, is the measure of how fast an object is moving and only has magnitude, such as a person running at 4 meters per second. In contrast, velocity, a vector quantity, includes both magnitude and direction, like a train traveling east at 55 meters per second. The script uses the example of a train crossing a 550-meter bridge in 10 seconds to illustrate how to calculate both speed and velocity. It emphasizes the importance of not confusing these terms and introduces the related concepts of distance and displacement. The video also touches upon real-life applications, providing average speeds for walking, running, cycling, and various modes of transportation, and briefly mentions the variable speeds of sound waves and wind. The script concludes by reminding viewers of the significance of understanding these concepts for various applications.
Takeaways
- 📏 **Speed vs. Velocity**: Speed is a scalar quantity that only has magnitude (e.g., 4 m/s running), while velocity is a vector quantity that includes both magnitude and direction (e.g., 6 m/s east cycling).
- 🔄 **Directional Importance**: Velocity includes direction, which is crucial for understanding motion, unlike speed, which does not.
- ⏱️ **Calculating Speed**: Speed is calculated by dividing the distance traveled by the time taken, resulting in a scalar value.
- 🚂 **Train Example**: For a train crossing a 550-meter bridge in 10 seconds, the speed is 55 meters per second.
- 📍 **Displacement for Velocity**: If the train's direction is known, displacement can be used to calculate velocity, which is a vector quantity.
- 🔄 **Negative Velocity**: Velocity can be negative, indicating motion in the opposite direction, which is not possible with speed.
- 🚶♂️ **Average Speed/Velocity**: For varying speeds during a journey, the total distance or displacement is divided by the total time to find the average speed or velocity.
- 🚗 **Real-Life Speeds**: Average speeds for walking, running, cycling, and vehicles are provided, highlighting that these can vary based on individual factors.
- ✈️ **Extreme Speeds**: Speeds for cars, fast trains, and planes are given, showing the range of speeds in different modes of transportation.
- 🌬️ **Wind and Sound**: The speed of wind and sound waves are mentioned, with the latter traveling at 330 m/s in air, a figure to remember.
- 🌡️ **Factors Affecting Wind Speed**: Wind speed can be influenced by temperature, atmospheric pressure, and structures, showing the variability of natural phenomena.
Q & A
What is the difference between speed and velocity?
-Speed is a scalar quantity that only conveys magnitude, such as how fast an object is moving. Velocity, on the other hand, is a vector quantity that includes both magnitude and direction, indicating not only how fast an object is moving but also the direction of its movement.
Why is it important to not confuse speed with velocity?
-Confusing speed with velocity can lead to incorrect calculations and misunderstandings in various contexts, such as physics problems or real-world applications. Speed only provides a measure of how fast an object is moving, while velocity provides both the rate and the direction, which is crucial for accurately describing motion.
What is the formula for calculating speed?
-The formula for calculating speed is the total distance traveled divided by the total time taken. It is expressed as Speed = Distance / Time.
How is velocity calculated and what units are used to express it?
-Velocity is calculated by taking the displacement (which includes direction) and dividing it by the time taken. It is expressed in units of distance per time, such as meters per second (m/s), and includes a directional component, like 'meters per second east'.
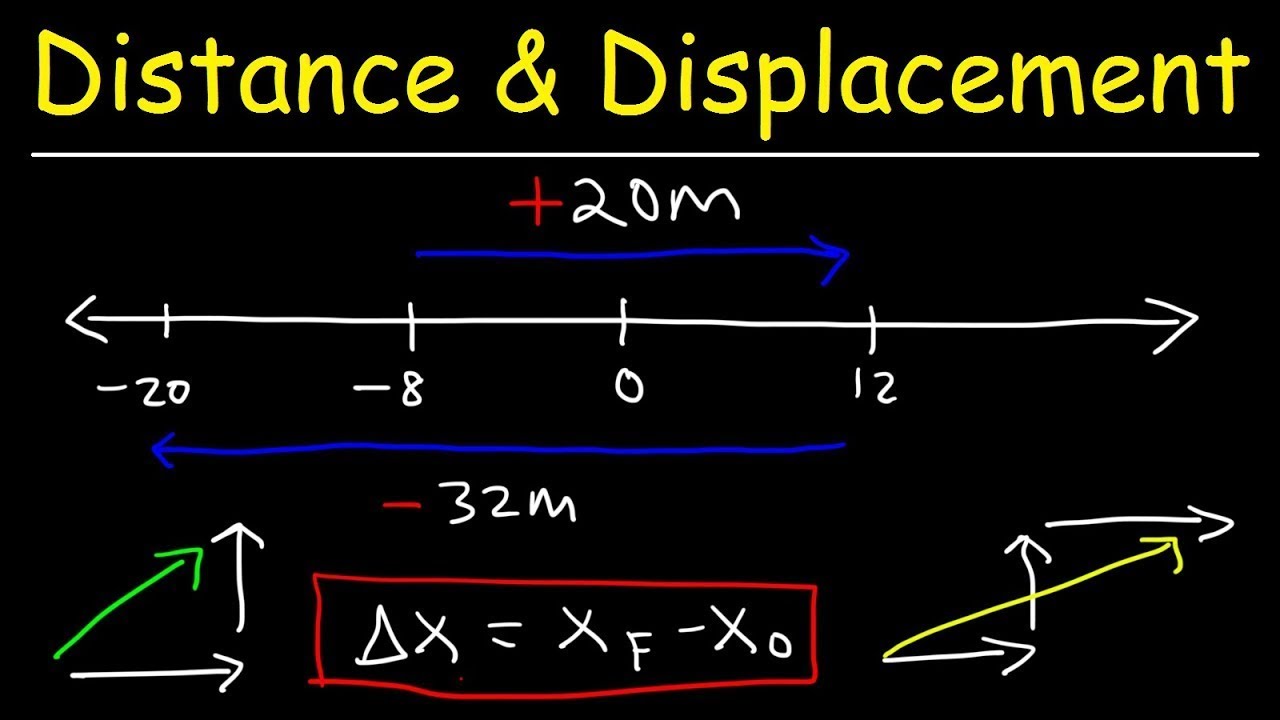
What is the difference between distance and displacement?
-Distance is a scalar quantity that only provides the magnitude of how far an object has traveled, without any regard to its direction. Displacement, however, is a vector quantity that considers both the magnitude and the direction of the object's movement.
How can we calculate the average speed or average velocity of an object?
-To calculate the average speed or average velocity, you divide the total distance or displacement traveled by the total time taken for the journey. This gives you an overall measure of the object's motion over the course of its path.
What are some real-life examples of speeds in meters per second?
-Some real-life speeds include people walking at about 1.5 m/s, running at around 3 m/s, and cycling at about 6 m/s. For vehicles, a car on the main road might travel around 25 m/s, a fast train could travel 55 m/s, and planes can exceed 250 m/s.
How does the speed of sound waves vary in different mediums?
-The speed of sound waves varies depending on the medium through which they are traveling. For example, sound waves travel at approximately 330 meters per second in air, but this speed changes when they move through different mediums like water.
What factors can affect the speed of the wind?
-The speed of the wind can be affected by various factors such as temperature, atmospheric pressure, and the structures that air flows past, like buildings or mountains.
Why might people use the velocity equation even when they do not have a direction?
-People might use the velocity equation even without a specified direction because it allows for the possibility of negative velocities, which can represent movement in the opposite direction. This can be useful in calculations where direction is not initially known or when accounting for reverse motion.
What is the significance of the units for speed and velocity?
-The units for speed and velocity (meters per second, m/s) indicate the rate of motion. For speed, it's a simple measure of how many meters are covered each second. For velocity, the units include a directional component, which specifies the direction of motion in addition to the rate.
How does the script differentiate between the symbols used for displacement and speed in formulas?
-In the formulas, the script uses 's' to represent displacement when discussing velocity, while in the speed equation, 's' stands for speed. The symbol 'd' is used to denote distance in both equations, and 't' stands for time.
Outlines
📏 Understanding Speed and Velocity
This paragraph introduces the concepts of speed and velocity, differentiating between them as scalar and vector quantities respectively. Speed is described as only having magnitude, such as a person running or a plane flying at a certain rate, while velocity includes both magnitude and direction, like cycling east or a train moving backwards. The importance of not confusing these terms for exams is emphasized. Additionally, the paragraph covers distance and displacement, with distance being a scalar and displacement being a vector. An example using a train crossing a bridge is provided to illustrate how to calculate speed and velocity. The potential for negative velocity to indicate backward movement is also mentioned.
🌬️ Varying Speeds in Nature and Transportation
The second paragraph discusses the variability of speeds in real-life scenarios, including the average speeds at which people walk, run, and cycle, as well as the speeds of vehicles like cars, trains, and planes. It also touches on the speed of sound waves in air and how it changes when traveling through different mediums, using the example of wind, which can vary significantly based on factors like temperature and atmospheric pressure. The paragraph concludes with a reminder of the speed of sound in air as an important figure to remember.
Mindmap
Keywords
💡Speed
💡Velocity
💡Scalar
💡Vector
💡Distance
💡Displacement
💡Average Speed
💡Average Velocity
💡Direction
💡Units
💡Real Life Speeds
Highlights
Speed and velocity are two distinct physical quantities; speed is a scalar with only magnitude, while velocity is a vector with both magnitude and direction.
Examples of speed include a person running at 4 meters per second and a plane flying at 250 meters per second.
Velocity examples include a person cycling east at 6 meters per second and a train moving backward at 55 meters per second.
It is common to confuse speed and velocity in exams, so it's crucial to understand the difference between them.
Distance is a scalar quantity that only provides magnitude, such as 10 meters or 40 miles.
Displacement is a vector quantity that includes direction, like running 40 meters east or a ball falling 2 meters down.
A train crossing a 550-meter long bridge in 10 seconds can be used to illustrate the calculation of speed and velocity.
Speed is calculated by dividing the distance traveled by the time taken, resulting in the scalar quantity of 55 meters per second for the train example.
Velocity calculation involves replacing distance with displacement and including direction, such as '550 meters east'.
The symbols used in velocity and speed equations can be confusing as 's' represents displacement in velocity and speed in the speed equation.
Velocity allows for negative values, indicating movement in the opposite direction.
Average speed or average velocity can be calculated by dividing total distance or displacement by total time taken for a journey.
Real-life examples of speeds include walking at about 1.5 meters per second, running at around 3 meters per second, and cycling at about 6 meters per second.
Vehicle speeds vary; for instance, a car on the main road might travel around 25 meters per second, a fast train at 55 meters per second, and planes can exceed 250 meters per second.
The speed of sound waves in air is 330 meters per second, a figure that is important to remember.
Wind speed, representing the natural movement of air, can vary from almost zero to faster than a speeding train and is influenced by factors like temperature and atmospheric pressure.
The video provides a comprehensive understanding of the concepts of speed, velocity, distance, and displacement, with practical examples and calculations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: