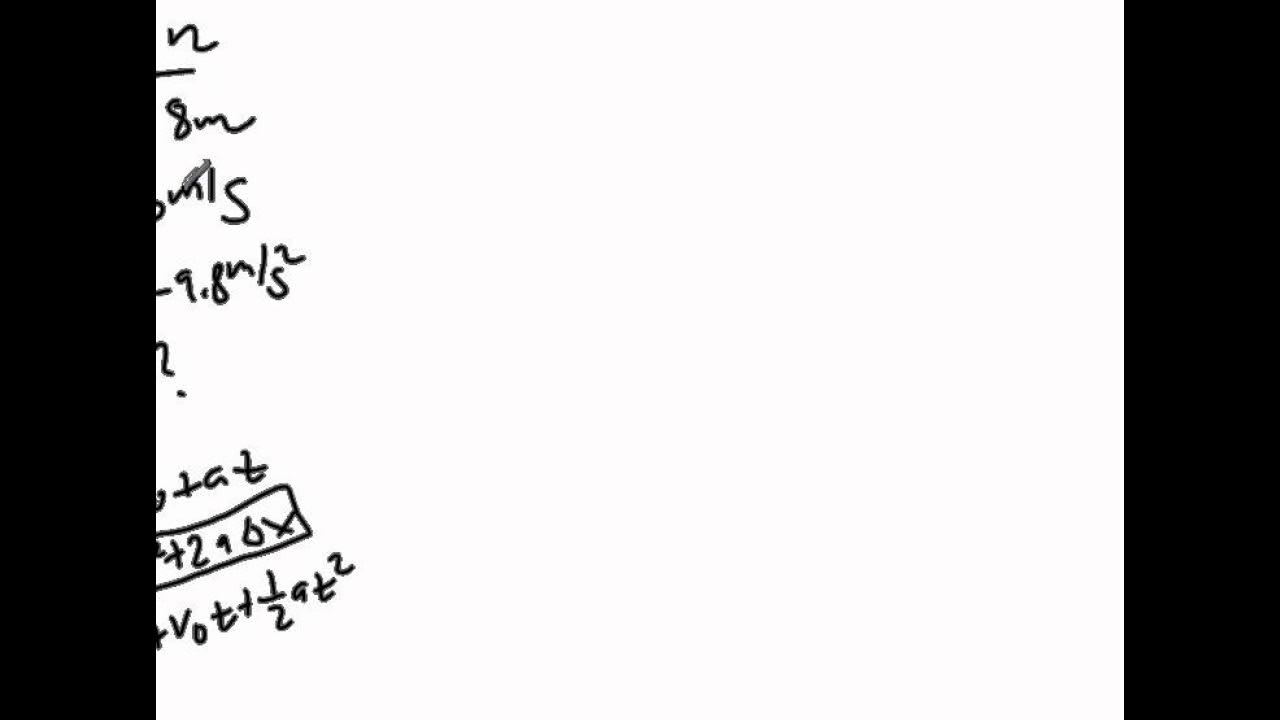DERIVE : s = ut + ½ at² | EQUATIONS OF MOTION (3)

BRAIN Academy

13 Aug 202303:28

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, the host derives the equation of motion 'S = ut + (1/2)at^2', starting with two fundamental formulas: distance 's = (u + v)/2 * t' and velocity 'v = u + at'. By substituting 'v' from the velocity formula into the distance formula, the host simplifies the equation to the classic kinematic equation, demonstrating a clear and concise method for understanding motion under constant acceleration.

Takeaways

📚 The video aims to derive an equation of motion, specifically S = UT + (1/2)aT^2.
🔍 Two fundamental formulas of motion are introduced: the formula for distance (S = (U + V)/2 * t) and the formula for final velocity (V = U + at).
🔧 The process involves manipulating these formulas to eliminate the variable V from the distance equation.
📝 The substitution of V with (U + at) from the second formula into the first formula is the key step in the derivation.
🧩 After substitution, the equation simplifies to S = U + (U + at) / 2 * t, which is then further simplified.
🔢 The simplification leads to S = 2UT + (1/2)at^2, which is then rearranged to the final form.
📉 The concept of dividing a sum by a constant (a + b)/c = a/c + b/c is used to simplify the equation.
📈 The final derived equation is S = UT + (1/2)aT^2, which relates initial velocity, acceleration, and time to the distance traveled.
👍 The video encourages viewers to like and subscribe if they find the content useful.
📚 The script is educational, providing a clear step-by-step explanation of how to derive the motion equation.

Q & A

What is the main topic of the video?
-The main topic of the video is deriving one of the equations of motion, specifically S = ut + (1/2)at^2.
What are the two formulas of motion mentioned in the video?
-The two formulas of motion mentioned are: 1) the formula for distance, which is s = (u + v) / 2 * t, and 2) the formula for final velocity, v = u + at.
Why is the final velocity (v) important in deriving the equation of motion?
-The final velocity (v) is important because it allows us to express the motion in terms of initial velocity (u) and acceleration (a), which are then used to derive the equation S = ut + (1/2)at^2.
How is the final velocity formula used to eliminate v from the distance formula?
-The final velocity formula (v = u + at) is substituted for v in the distance formula to eliminate v and express the equation solely in terms of u, a, and t.

Outlines

00:00

📚 Introduction to Deriving the Motion Equation

The video begins with a warm welcome to the channel and introduces the goal of deriving a specific motion equation, S = UT + (1/2)aT^2. The presenter mentions the necessity of understanding two fundamental motion formulas: the distance formula, S = (U + V) / 2 * t, and the relationship between initial velocity, final velocity, and acceleration, V = U + aT. The intention is to eliminate the final velocity, V, from the equation by substituting it with the expression derived from the second formula.

🔍 Substituting to Remove Final Velocity

This paragraph delves into the process of eliminating the final velocity, V, from the distance equation by substituting it with the expression from the second formula. The presenter demonstrates the algebraic manipulation by replacing V with (U + aT) and then simplifying the equation step by step. The explanation involves basic algebraic principles, such as factoring and combining like terms, to reach a simplified form of the motion equation.

📝 Simplifying to Obtain the Desired Equation

The presenter continues with the simplification process, showing how to derive the final motion equation by dividing terms and using algebraic identities. The explanation includes breaking down the equation into simpler components and then recombining them to form the desired equation, S = UT + (1/2)aT^2. The presenter emphasizes the logic behind the simplification, comparing it to basic division and addition of fractions with the same denominator.

🎉 Conclusion and Call to Action

The final paragraph wraps up the video with the successfully derived motion equation and invites viewers to like and subscribe to the channel if they found the content useful. The presenter thanks the audience for watching and provides a brief recap of the derived equation, reinforcing the educational value of the video.

Mindmap

Keywords

💡Equation of Motion

An equation of motion is a mathematical relationship that describes the motion of an object under the influence of various forces. In the context of this video, the equation derived is a specific case of motion under constant acceleration. The video's main theme revolves around deriving the equation S = UT + (1/2)at^2, which is a fundamental equation in kinematics.

💡Derive

To derive in a mathematical sense means to obtain a formula or equation from other known formulas or principles. The video demonstrates the process of deriving the equation of motion by using two known motion formulas, illustrating the concept of derivation in the context of physics.

💡Distance

Distance is a measure of the interval between two points in space, typically measured in units like meters or kilometers. In the script, the formula for distance (S = (U + V)/2 * t) is one of the starting points for deriving the motion equation, showing its relevance to the theme of motion analysis.

💡Velocity

Velocity is a vector quantity that represents the rate of change of an object's position with respect to time. The script introduces two velocities: initial velocity (U) and final velocity (V), which are essential components in the equations used to derive the motion equation.

💡Acceleration

Acceleration is the rate at which an object's velocity changes over time. In the script, the term 'a' represents acceleration, and the formula V = U + at is used to express the relationship between velocity, initial velocity, and acceleration in uniformly accelerated motion.

💡Formula

A formula in this context refers to a mathematical expression used to describe a relationship between variables. The video script mentions two formulas of motion that are prerequisites for deriving the final equation, emphasizing the importance of formulas in physics.

💡Uniformly Accelerated Motion

Uniformly accelerated motion is a type of motion where an object's acceleration is constant. The video's derived equation, S = UT + (1/2)at^2, is specifically for this type of motion, highlighting a common scenario in kinematics where the acceleration does not change.

💡Integration

Although not explicitly mentioned, the process of deriving the equation in the video involves a form of mathematical integration, where the area under the velocity-time graph (which represents displacement) is calculated using the formula for uniformly accelerated motion.

💡Algebraic Manipulation

Algebraic manipulation refers to the process of rearranging and combining mathematical expressions to simplify or transform them. The video demonstrates this by substituting and simplifying the equations to derive the final motion equation.

💡Substitution

Substitution is a method used in algebra where one expression is replaced with another to simplify a formula or equation. In the script, the final velocity (V) is substituted with the expression from the second formula to eliminate it from the first equation, leading to the derived equation.

💡Simplification

Simplification in mathematics is the process of making a complex expression or equation more straightforward. The video script shows simplification steps, such as dividing terms and combining like terms, to arrive at the simplified motion equation.

Highlights

Introduction to deriving an equation of motion

Equation to be derived: S = UT + (1/2)AT^2

Two formulas of motion required for derivation

First formula: S = (U + V) / 2 * t

Second formula: V = U + AT

Objective to eliminate V from the equation

Substitution of V with the second formula

Simplification of the equation by replacing V

Expression of S in terms of U, A, and t

Multiplication of terms with time (t)

Division and simplification of the equation

Use of algebraic properties to simplify the expression

Final derived equation: S = UT + (1/2)AT^2

Explanation of the algebraic process used

Cancellation of terms and addition for simplification

Finalization of the derived motion equation

Encouragement to like and subscribe for more content

Transcripts

Browse More Related Video

How to Derive the Equations of Motion (Derivation)

AP Physics B Kinematics Presentation #32

Equations of Motion (Physics)

AP Physics B Kinematics Presentation #03

AP Physics B Kinematics Presentation #21

AP Physics B Kinematics Presentation #31