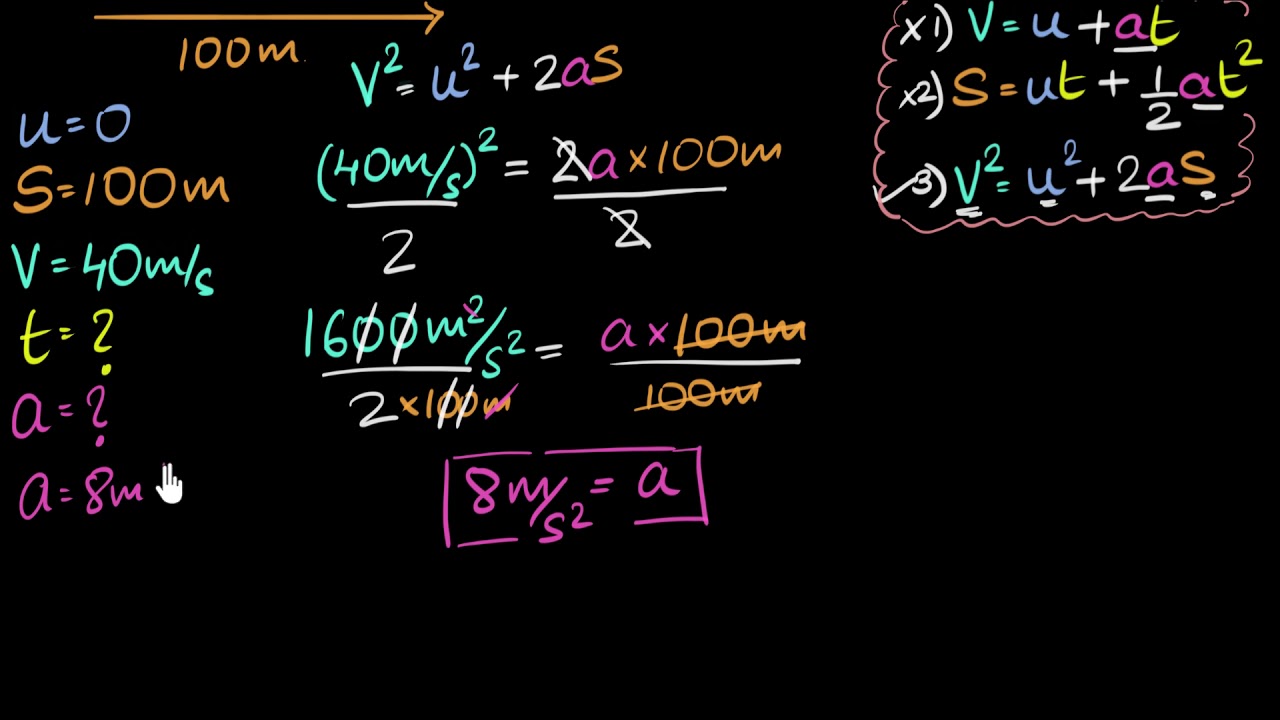AP Daily: AP Physics C: Mechanics (1.1)

Advanced Placement
3 Sept 202009:23
EducationalLearning
32 Likes 10 Comments

TLDRIn this AP Physics video, Dr. Julie Hood from MAST Academy explains kinematics in one dimension, focusing on calculating unknown variables like acceleration, velocity, and position for uniformly accelerated motion. She uses a practical problem involving two cars: one speeding at 40 m/s and another accelerating from rest at 2 m/s². Dr. Hood demonstrates solving the problem using motion diagrams, graphical analysis, and equations of motion, finding the time and distance needed for the accelerating car to catch the speeder. She encourages viewers to try a more complex problem and previews the next lesson on acceleration due to gravity.

Takeaways
  • 📚 The video is an educational resource for AP Physics, focusing on kinematics and motion in one dimension.
  • 🏎️ The scenario involves two cars: Car 1 is at a pit stop and Car 2 is moving at a constant speed of 40 meters per second.
  • 🔧 Car 1 starts from rest and accelerates at a rate of 2 meters per second squared to catch up with Car 2.
  • ⏱️ The main questions are to determine the time it takes for Car 1 to overtake Car 2 and the distance Car 2 travels before being overtaken.
  • 📈 The video introduces the use of motion diagrams and graphical analysis to visualize and solve physics problems.
  • 📘 It emphasizes the importance of being familiar with the equations of motion, particularly those for uniform acceleration.
  • 📊 The position-time graph for Car 2 is a straight line with a slope equal to its velocity, while Car 1's graph is parabolic due to acceleration.
  • 🔢 By setting the position equations for both cars equal to each other, the time and distance can be calculated when they meet.
  • 🕒 It takes 40 seconds for Car 1 to catch up with Car 2, and they have both traveled 1600 meters by that time.
  • 🛣️ The video also discusses a more realistic scenario where Car 1 can only accelerate up to a maximum speed before maintaining it to catch Car 2.
  • 🔄 The importance of double-checking work using different methods, such as graphical analysis and equations, is highlighted for accuracy.
Q & A

  • What is the main topic discussed in the video by Dr. Julie Hood?

    -The main topic discussed in the video is kinematics motion in one dimension, specifically calculating unknown variables of motion for an object undergoing uniform accelerated motion.

  • What are the different representations of motion that Dr. Hood mentions to solve physics problems?

    -Dr. Hood mentions motion diagrams, graphical analysis, and the equations of motion as the different representations to solve physics problems.

  • What is the scenario presented in the problem discussed by Dr. Hood?

    -The scenario involves Car 1 at a pit stop getting its tire pressure adjusted while Car 2 speeds by at a constant rate. Car 1 starts accelerating from rest to catch up with Car 2.

  • What is the constant rate at which Car 2 is traveling?

    -Car 2 is traveling at a constant rate of 40 meters per second.

  • What is the acceleration rate of Car 1 from rest?

    -Car 1 accelerates from rest at a rate of 2 meters per second squared.

  • What are the two equations of motion that Dr. Hood uses to solve the problem?

    -The two equations of motion used are for uniform acceleration: one for the car moving at a constant speed (distance equals rate times time) and one for the car accelerating (position equals one-half acceleration times time squared).

  • How long does it take for Car 1 to catch up with Car 2 according to the problem?

    -It takes 40 seconds for Car 1 to catch up with Car 2.

  • How far has Car 2 traveled by the time it is overtaken by Car 1?

    -By the time Car 1 catches up, Car 2 has traveled 1600 meters.

  • What is the significance of the slope on a position-time graph in the context of the video?

    -The slope on a position-time graph represents the velocity of the object. For a constant velocity, it's the slope of the line, and for an accelerating object, it's the slope of the tangent to the curve at any given time.

  • What is the maximum speed Car 1 can reach in the modified scenario mentioned by Dr. Hood?

    -In the modified scenario, Car 1 can reach a maximum speed of 60 meters per second.

  • What is the speed of Car 1 when it finally catches up with Car 2 in the modified scenario?

    -In the modified scenario, Car 1 must reach a speed of 80 meters per second to catch up with Car 2, which is twice the speed of Car 2.

  • What advice does Dr. Hood give for students preparing for the AP Physics exam?

    -Dr. Hood advises students to get very familiar with the equation sheet provided during the AP Physics exam and to double-check their work using different methods such as graphical analysis and equations of motion.

Outlines
00:00
🚗 Kinematics and Motion Calculations

In this segment, Dr. Julie Hood introduces the topic of kinematics, focusing on one-dimensional motion. The video aims to calculate variables such as acceleration, velocity, and position for an object undergoing uniform acceleration from rest. Dr. Hood emphasizes the importance of understanding different representations of motion, including motion diagrams, graphical analysis, and equations of motion. A specific problem is presented involving two cars, one accelerating from rest at a rate of 2 m/s² and the other moving at a constant speed of 40 m/s. The goal is to determine the time and distance when the accelerating car catches up to the constant speed car. The equations of motion relevant to uniform acceleration are highlighted, and a visual representation of the problem is provided, showing the parabolic nature of the accelerating car's position over time and the linear motion of the constant speed car. The video concludes with a graphical solution to the problem, indicating that it takes 40 seconds for the accelerating car to catch up and that both cars have traveled 1600 meters by that time.

05:00
📚 Solving Physics Problems with Motion Analysis

This paragraph delves deeper into solving the physics problem presented earlier using equations and graphical analysis. Dr. Hood explains the equations for both cars, with Car 2 having a constant speed of 40 m/s and Car 1 starting from rest with an acceleration of 2 m/s². The equations are set equal to each other to find the time it takes for Car 1 to catch Car 2, which is 40 seconds, and the distance covered, which is 1600 meters. The importance of double-checking work using different methods, such as substitution into the equations or graphical analysis, is stressed. The paragraph also discusses the concept of velocity represented by the slope of a position-time graph, and how the accelerating car's velocity at the moment of catching up is twice that of the constant speed car, reaching 80 m/s. Dr. Hood then introduces a more complex scenario where Car 1 can only accelerate up to a maximum speed of 60 m/s, after which it maintains that speed until catching Car 2. She encourages viewers to try this problem at home and provides a graphical analysis as a hint. The segment wraps up with an invitation to the next video, which will cover acceleration due to gravity.

Mindmap
Keywords
💡Kinematics
Kinematics is the branch of physics that deals with the motion of objects without considering the forces that cause the motion. In the video, kinematics is the central theme, as the motion of two cars is analyzed in terms of their velocity, acceleration, and position over time. The script discusses how kinematics helps in understanding the motion of the speeding car and the accelerating car.
💡Uniform Accelerated Motion
Uniform accelerated motion refers to the motion of an object whose acceleration is constant. The video script uses this concept to describe the motion of car one, which accelerates at a constant rate from rest. The concept is essential in understanding how car one catches up to car two, which is moving at a constant speed.
💡Acceleration
Acceleration is the rate of change of velocity of an object. In the script, car one has an acceleration of two meters per second squared, which means its speed increases by two meters per second every second. The concept of acceleration is crucial in determining the time it takes for car one to catch car two.
💡Velocity
Velocity is the speed of an object in a specific direction. The video script mentions that car two has a constant velocity of 40 meters per second, while car one's velocity changes due to acceleration. Understanding velocity is key to analyzing the relative motion of the two cars.
💡Position
Position refers to the location of an object in space. In the context of the video, the script uses position to describe where the cars are at any given time. The equations of motion are used to calculate the position of car one and car two at the moment they meet.
💡Equations of Motion
The equations of motion are formulas that describe the relationship between an object's displacement, velocity, acceleration, and time. The script specifically uses two of these equations to solve the problem of when and where car one catches car two. These equations are fundamental to the analysis of the cars' motion.
💡Graphical Analysis
Graphical analysis is a method of solving physics problems by using graphs to visualize and solve for variables. In the video, the script describes how the position-time graph of car one is a parabola, and car two's is a straight line, which visually helps to determine when and where they meet.
💡Motion Diagrams
Motion diagrams are visual representations that help to understand the motion of objects. The script mentions using motion diagrams to visualize constant velocity and accelerating objects, aiding in the comprehension of the cars' movements.
💡Slope
In the context of position-time graphs, slope represents velocity. The script explains that the slope of the line for car two indicates its constant velocity, while the slope of the tangent to the curve for car one gives its instantaneous velocity at any given time.
💡Parabolic Motion
Parabolic motion describes the path of an object undergoing uniformly accelerated motion from rest. The script uses this term to describe the position-time graph of car one, which is a parabola, indicating that its position changes quadratically with time.
💡Maximum Speed
Maximum speed is the highest velocity an object can reach. In the script, a variation of the problem is presented where car one can only accelerate until it reaches a maximum speed of 60 meters per second, after which it maintains that speed to catch car two. This concept is important for understanding the limitations on acceleration.
Highlights

Introduction to the topic of kinematics motion in one dimension.

Exploration of calculating unknown variables of motion for an object undergoing uniform accelerated motion.

Use of different representations of motion to solve physics problems including motion diagrams and graphical analysis.

Explanation of the equations of motion relevant to the problem presented.

Description of a scenario involving car one and car two to illustrate the concept of uniform acceleration.

Graphical representation of the motion of a speeding car and an accelerating car.

Understanding that the slope of a position-time graph represents velocity.

Demonstration of the difference between linear and parabolic motion on a position-time graph.

Solving the problem of when and where car one catches up to car two using both graphical and algebraic methods.

Emphasis on the importance of double-checking work using different methods to ensure accuracy.

Calculation of the speed of the accelerating car at the moment it catches the speeder.

Introduction of a more realistic problem involving a car that can only accelerate up to a maximum speed.

Encouragement for viewers to try the problem at home and provide a graphical analysis as a hint.

Conclusion summarizing the use of different representations to solve physics problems effectively.

Invitation to join the next video on the topic of acceleration due to gravity.

Transcripts

Browse More Related Video

3 | FRQ | Practice Sessions | AP Physics C: Mechanics

1 | MCQ | Practice Sessions | AP Physics C: Mechanics

Using equations of motion (2 steps numerical)

2 | FRQ | Practice Sessions | AP Physics C: Mechanics

Circular Motion Ferris Wheel Problem

AP Physics Workbook 1.J Vertrical Motion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
KinematicsMotionPhysicsAccelerationVelocityPositionUniform AccelerationGraphical AnalysisEquations of MotionEducationalAP Daily