Equilibrium of a Particle (2D x-y plane forces) | Mechanics Statics | (Learn to solve any question)
TLDRThe video script delves into the concept of equilibrium for a particle, focusing on coplanar forces within the x-y plane. It explains the necessity for all forces acting on an object to sum to zero for it to remain at rest. The script introduces Hooke's Law for springs, emphasizing the spring's stiffness and elongation, and highlights that cables can only support tension, not compression. Weight, as the product of mass and gravity, is consistently downward, regardless of the object's incline. The video progresses through various examples, illustrating how to calculate unknown forces in equilibrium situations, including a cylinder suspended by wires, a pipe supported by multiple cables, and a crate held by a spring and cable. It concludes with a geometric problem involving a single cable and a sack, showcasing the application of trigonometric principles. The script promises a follow-up video on solving 3D equilibrium problems, encouraging viewers to continue their educational journey.
Takeaways
- 📚 Equilibrium describes a state where an object is not moving, such as a flower pot hung on the ceiling or a picture frame on a wall.
- 📐 In coplanar force systems, equilibrium is achieved when the sum of all forces along the x-axis and y-axis equal zero.
- 🔍 To solve for unknown forces, forces must be broken down into their x and y components using trigonometric functions like cosine and sine.
- 🤔 Hooke's Law (F = Ks) is used to determine the force in a spring, where K is the spring's stiffness and s is the elongation or compression.
- 🚫 A cable can only support tension and not compression; it cannot push, only pull, and the force will always act in the direction of the cable.
- 📈 The tension in a cable running through a pulley remains constant throughout the cable's length.
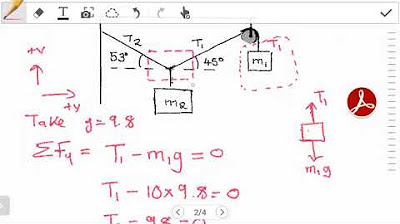
- 📉 An object's weight is calculated by multiplying its mass by the acceleration due to gravity (9.81 m/s² or 32.2 ft/s²) and acts vertically downward.
- 📈 When solving problems, it's essential to draw a free body diagram and select an appropriate point to write out equations of equilibrium.
- 🔢 In problems with multiple points, it's necessary to write equations of equilibrium for each point and express each force in terms of a single known value, like weight, for comparison.
- 🔍 To find the maximum mass that can be supported, compare the calculated tensions in different cables and solve for the mass that causes one of the tensions to reach its maximum allowable value.
- 📐 For problems involving springs, calculate the angles and use the Pythagorean theorem to find the stretched length of the spring, then apply Hooke's Law to find the stiffness.
- 🔬 In more geometrically complex problems, use the properties of triangles and trigonometry to find unknown lengths and angles, which can then be used to determine forces and tensions.
Q & A
What is the term 'equilibrium' used to describe in the context of physics?
-In physics, 'equilibrium' describes a state where an object is not moving, meaning all the forces acting on it are balanced so that the net force is zero.
What are coplanar forces?
-Coplanar forces are a system of forces that act entirely within the same plane, such as the x-y plane.
How do you determine the tension in a cable supporting an object in equilibrium?
-To determine the tension in a cable, you need to write equations of equilibrium for both the x-axis and y-axis forces, ensuring that the sum of all components in each direction equals zero.
What is Hooke's Law and how is it used?
-Hooke's Law states that the force (F) needed to compress or stretch a spring is directly proportional to the displacement (s) from its equilibrium position, expressed as F = k*s, where k is the spring's stiffness constant.
Why can a cable only support tension and not compression?
-A cable can only support tension because its structure allows it to withstand pulling forces but not pushing forces, as you cannot push on a rope.
What is the formula for calculating the weight of an object?
-The weight (W) of an object is calculated by multiplying its mass (m) by the acceleration due to gravity (g), which is approximately 9.81 m/s², so the formula is W = m*g.
How do you determine the components of a force acting at an angle?
-The components of a force acting at an angle can be determined using trigonometric functions: the x-component is found using the cosine of the angle, and the y-component is found using the sine of the angle.
What is the process for solving for unknown forces in a system with multiple points of support?
-To solve for unknown forces, you would write equations of equilibrium for each point of support, considering the forces acting on that point. Then, you would solve the system of equations to find the unknown forces.
How do you find the maximum mass that a system of cables can support?
-To find the maximum mass, you would first determine the maximum tension each cable can support, then write equations of equilibrium for the forces acting on the system. By solving these equations, you can find the mass that would cause one of the tensions to reach its maximum allowable value.
What is the significance of writing forces in terms of weight in a problem?
-Writing forces in terms of weight simplifies the comparison of forces acting on the system and allows for a straightforward determination of which cable or component will experience the greatest force.
How can you find the stiffness of a spring given the force and the amount it is stretched?
-You can find the stiffness (k) of a spring using Hooke's Law, rearranged to solve for k: k = F/s, where F is the force applied to the spring and s is the amount it is stretched or compressed.
In a problem involving geometry and equilibrium, how can you use the angles and lengths to find the unknowns?
-In a geometry problem, you can use trigonometric relationships and the Pythagorean theorem to relate the angles and lengths of the system. By setting up and solving equations based on these relationships, you can find the unknown values such as the tension in a cable or the position of a point.
Outlines
📐 Understanding Equilibrium and Coplanar Forces
This paragraph introduces the concept of equilibrium, which is a state of rest where the net force on an object is zero. It discusses coplanar forces, which are forces acting within the same plane, and how to resolve them into x and y components to maintain equilibrium. The importance of breaking down forces into components and summing them to zero for both axes is emphasized. The paragraph also touches on the behavior of springs, governed by Hooke's Law, and the characteristics of cables that can only support tension. Finally, it mentions the concept of weight as the force due to gravity acting on an object's mass.
🧮 Solving for Unknown Forces in Equilibrium
The second paragraph delves into solving equilibrium problems by setting up equations based on the forces acting on a body. It illustrates the process with an example involving a cylinder in equilibrium, highlighting the need to select a point of reference and draw a coordinate system to analyze the forces. The forces considered include the tension in wires and the weight of the object. The paragraph explains how to calculate the components of each force and set up equations for both the x-axis and y-axis forces. It also demonstrates how to solve these equations to find the unknown tensions in the cables. The discussion extends to a problem involving multiple points, where the maximum tension each cable can support is given, and the largest mass of a pipe that can be supported is to be found. The process involves writing equations for each point, isolating variables, and solving for the mass. The paragraph concludes with an example involving a spring, where the stiffness needed to hold a crate in position is calculated using Hooke's Law, and the extension of the spring is determined using the Pythagorean theorem.
Mindmap
Keywords
💡Equilibrium
💡Coplanar Forces
💡Tension
💡Hooke's Law
💡Cable Direction
💡Weight
💡Free Body Diagram
💡Components of Force
💡Vector Addition
💡Maximum Tension
💡Stiffness
💡Pythagorean Theorem
Highlights
Equilibrium describes an object that is not moving, such as a flower pot hung on the ceiling or a picture frame on a wall.
Coplanar forces are a system of forces that lie in the x-y plane, and equilibrium equations for these forces must equal zero for an object to remain at rest.
Each force acting on an object in equilibrium must be broken down into x and y components and summed to zero.
Hooke's Law (F = Ks) is used to determine the force in a spring when it is stretched or compressed, where K is the spring's stiffness and s is the elongation or compression.
Cables can only support tension and the force acts in the direction of the cable; the tension is the same throughout the cable if it passes through a pulley.
The weight of an object is calculated as the mass of the object times the acceleration due to gravity (9.81 m/s^2 or 32.2 ft/s^2) and is always directed straight down.
When solving for unknown forces in equilibrium, select a point to write out equations of equilibrium and draw a coordinate system to represent forces.
Force components in equilibrium problems can be found using trigonometric functions like cosine and sine.
In problems with multiple points, the maximum tension a cable can support can be determined by comparing forces and solving equations of equilibrium.
The force in a spring can be calculated using the Pythagorean theorem and Hooke's Law after finding the spring's stretched length.
In problems involving geometry, alternate interior angles and the total length of a cable can be used to find unknown values like the tension in a cable.
Free body diagrams are essential for visualizing and solving equilibrium problems, especially when multiple forces and angles are involved.
The maximum mass that can be supported by a system can be found by solving for the weight that causes a specific force to equal the maximum tension.
Equations of equilibrium for both x and y-axis forces are crucial for solving 2D equilibrium problems.
In the next video, 3-dimensional equilibrium problems will be discussed, expanding on the concepts learned in 2D.
The video concludes with a reminder to apply the knowledge gained to solve various types of equilibrium problems and encourages viewers in their studies.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: