Finding the Area Under the ROC Curve — Topic 91 of Machine Learning Foundations

Jon Krohn
9 Mar 202203:40
EducationalLearning
32 Likes 10 Comments

TLDRThe video script outlines a practical demonstration of calculating the area under the Receiver Operating Characteristic (ROC) curve using Python code. It emphasizes the significance of the ROC curve as a comprehensive metric for evaluating binary classification models in machine learning. The demonstration employs the trapezoidal rule through the `auc` method from the scikit-learn library, utilizing five given coordinate points to approximate the area under the curve. The result, an area of 0.75, is visually confirmed against a chart provided in the video. This exercise concludes the calculus content in the speaker's machine learning foundation series, with a promise of a summary video and recommended resources for further exploration into calculus.

Takeaways
  • 📈 The video demonstrates how to calculate the area under the Receiver Operating Characteristic (ROC) curve using Python code.
  • 🧮 The ROC curve is a powerful metric used in machine learning to evaluate the quality of a binary classification model.
  • 📊 The area under the ROC curve is calculated using integral calculus, specifically the trapezoidal rule, which is a numerical approach.
  • 📚 The scikit-learn library's `metrics` module provides an `auc` method that can be used to find the area under the curve.
  • 📍 Five specific coordinates (0,0), (0,0.5), (0.5,0.5), (0.5,1), and (1,1) are used to represent the ROC curve for the calculation.
  • 💻 The video is a part of a machine learning foundation series focusing on integration and its application in machine learning.
  • 🔗 The method uses numerical integration to approximate the area under the curve when an explicit function is not available.
  • 📝 The coordinates are input into the `auc` method as two vectors of x and y values to calculate the area.
  • 🔢 The calculated area under the curve in the example is 0.75, which can be visually confirmed by the chart provided.
  • 🔍 The video concludes with a suggestion to look at the chart to verify the calculated area and understand the concept better.
  • 🚀 The next video in the series will summarize the calculus content covered and provide resources for further learning.
Q & A

  • What is the purpose of the video?

    -The video demonstrates how to calculate the area under the Receiver Operating Characteristic (ROC) curve using Python code, which is a machine learning specific application of integral calculus.

  • What is the Receiver Operating Characteristic (ROC) curve?

    -The ROC curve is a graphical representation that allows for the assessment of the quality of a binary classification model by plotting the true positive rate against the false positive rate at various threshold settings.

  • How does the video use integral calculus to find the area under the ROC curve?

    -The video uses the numerical approach of the trapezoidal rule from the scikit-learn metrics module to calculate the area under the curve.

  • What is the numerical method used to calculate the area under the curve?

    -The trapezoidal rule is used, which is a numerical integration technique that approximates the area under a curve as a series of trapezoids.

  • How many coordinates are used in the video to calculate the area under the ROC curve?

    -Five coordinates are used to calculate the area under the ROC curve.

  • What are the five coordinates used in the video?

    -The five coordinates are (0,0), (0,0.5), (0.5,0.5), (0.5,1), and (1,1).

  • How does the video approach the problem of not having a function to calculate the area under the curve?

    -The video uses the available xy-coordinates and the auc method from the scikit-learn metrics module to numerically calculate the area under the curve.

  • What is the area under the ROC curve calculated in the video?

    -The area under the ROC curve calculated in the video is 0.75.

  • How can the calculated area under the ROC curve be visually confirmed?

    -The calculated area can be visually confirmed by looking at the chart provided in the video, where three quarters of the area under the ROC curve is filled in.

  • What is the next step after the calculus content in the machine learning foundation series?

    -The next step is a quick summary of everything covered in the series, followed by a list of the presenter's favorite resources for further study into calculus topics.

  • Why is the ROC curve considered a nuanced and powerful metric?

    -The ROC curve is considered nuanced and powerful because it provides a single summary metric that encapsulates the trade-off between the true positive rate and the false positive rate, offering a comprehensive view of a classification model's performance.

  • What is the significance of the area under the ROC curve in machine learning?

    -The area under the ROC curve is significant because it quantifies the overall ability of a classification model to distinguish between classes. An area of 1 indicates a perfect model, while an area of 0.5 suggests the model is no better than random guessing.

Outlines
00:00
📈 Calculating the Area Under the ROC Curve

This paragraph introduces the application of integral calculus to machine learning by calculating the area under the Receiver Operating Characteristic (ROC) curve. The ROC curve is a powerful metric for assessing the quality of a binary classification model. The video demonstrates a hands-on, automated approach using Python code. It guides viewers to a specific section of a Jupyter notebook where the calculation takes place. The process involves using numerical integration, specifically the trapezoidal rule, to calculate the area under the curve from given coordinates. The scikit-learn library's 'auc' method is used for this purpose. The video concludes by confirming the calculated area of 0.75 visually against a chart and mentions a forthcoming summary of calculus content in the machine learning foundation series.

Mindmap
Keywords
💡Python code
Python code refers to the programming language used in the video to demonstrate the calculation of the area under the ROC curve. It is a high-level, interpreted language known for its readability and is widely used in machine learning and data analysis. In the context of the video, Python code is used to perform a hands-on demonstration, which is a core part of the educational content.
💡Area under the curve (AUC)
The Area under the curve (AUC) is a statistical measure used to evaluate the performance of a binary classification model. It is calculated by integrating the ROC curve, which plots the true positive rate against the false positive rate at various threshold settings. In the video, the AUC is the primary metric being calculated to assess the quality of a given binary classification model.
💡Receiver Operating Characteristic (ROC)
The Receiver Operating Characteristic (ROC) is a graphical plot used in statistical analysis to illustrate the diagnostic ability of a binary classifier system. It is created by plotting the true positive rate (sensitivity) against the false positive rate (1 - specificity) at various threshold levels. In the video, the ROC curve is a central concept, as the area under this curve is being calculated to evaluate the model's performance.
💡Machine Learning
Machine Learning is a field of artificial intelligence that involves the use of data and algorithms to parse data, learn from that data, and make informed decisions based on what they've learned. The video is a machine learning specific example, meaning it applies the concepts of machine learning to understand and calculate the AUC of a classification model.
💡Integral Calculus
Integral calculus is a branch of mathematics that deals with the concept of integration, which is used to calculate areas and volumes. In the video, integral calculus is applied to calculate the area under the ROC curve, which is a key part of the demonstration. The use of calculus here shows how mathematical principles can be applied to real-world problems in machine learning.
💡Trapezoidal Rule
The trapezoidal rule is a numerical method used to approximate the definite integral of a function. It is particularly useful when dealing with a discrete set of data points, as it calculates the area under the curve by breaking it into trapezoids. In the video, the trapezoidal rule is used to calculate the AUC under the ROC curve, which is demonstrated through the Python code.
💡Scikit-learn
Scikit-learn is a popular machine learning library in Python that provides a range of tools for data analysis and model building. In the video, the scikit-learn library's metrics module is used to calculate the AUC, showcasing how this library can be leveraged for machine learning tasks.
💡Numerical Approach
A numerical approach refers to the method of finding approximate solutions to mathematical problems using numerical techniques, as opposed to symbolic or analytical methods. In the context of the video, a numerical approach is used to calculate the AUC under the ROC curve when an explicit function is not available, which is done through the trapezoidal rule.
💡Coordinates
Coordinates are pairs of numbers that define a point's position in a space. In the video, five specific coordinate points (0,0), (0,0.5), (0.5,0.5), (0.5,1), and (1,1) are used to calculate the area under the ROC curve. These coordinates represent the points on the ROC curve and are essential for the numerical integration process.
💡Vectors
In the context of the video, vectors refer to arrays or lists of elements, specifically the x-coordinates and y-coordinates of the points on the ROC curve. These vectors are used as inputs to the AUC calculation method from the scikit-learn library, demonstrating how data can be organized and processed in Python.
💡Colab Notebook
A Colab Notebook is an interactive online platform that allows users to write and execute Python code in a collaborative environment. In the video, the Colab Notebook is used to run the Python code for calculating the AUC under the ROC curve, highlighting its utility for machine learning experiments and demonstrations.
Highlights

The video demonstrates calculating the area under the Receiver Operating Characteristic (ROC) curve using Python code.

The ROC curve is a nuanced and powerful summary metric for assessing the quality of a binary classification model in machine learning.

The area under the ROC curve is calculated using integral calculus, specifically the trapezoidal rule.

The demonstration uses five specific coordinates to calculate the area under the curve.

The scikit-learn library's metrics module provides an 'auc' method for numerical integration.

The 'auc' method is applied to two vectors of x and y coordinates to find the area under the curve.

The result of the area under the curve is 0.75, which can be visually confirmed on the provided chart.

The video is part of a machine learning foundation series that covers integration in calculus.

The video provides a hands-on code demo for a quick and automated calculation of the area under the ROC curve.

The coordinates used in the demo are (0,0), (0,0.5), (0.5,0.5), (0.5,1), and (1,1).

The integration process involves creating vectors for x and y coordinates and using them in the 'auc' method.

The video concludes with a summary of the calculus content covered in the machine learning foundation series.

The next video in the series will provide a summary and resources for further study of calculus topics.

The numerical approach used in the demo is based on the trapezoidal rule, which can be explored further in the provided link.

The video assumes prior knowledge of the ROC curve from earlier segments in the series.

The integration is performed using a Jupyter notebook, which is a popular tool for data analysis and machine learning.

The video emphasizes the practical application of calculus in the context of machine learning model evaluation.

The hands-on demo shows how to run the Jupyter notebook and execute the necessary code cells.

The final section of the Jupyter notebook is dedicated to calculating the area under the ROC curve.

The video provides a clear, step-by-step guide on how to perform the calculation using Python and scikit-learn.

Transcripts

Browse More Related Video

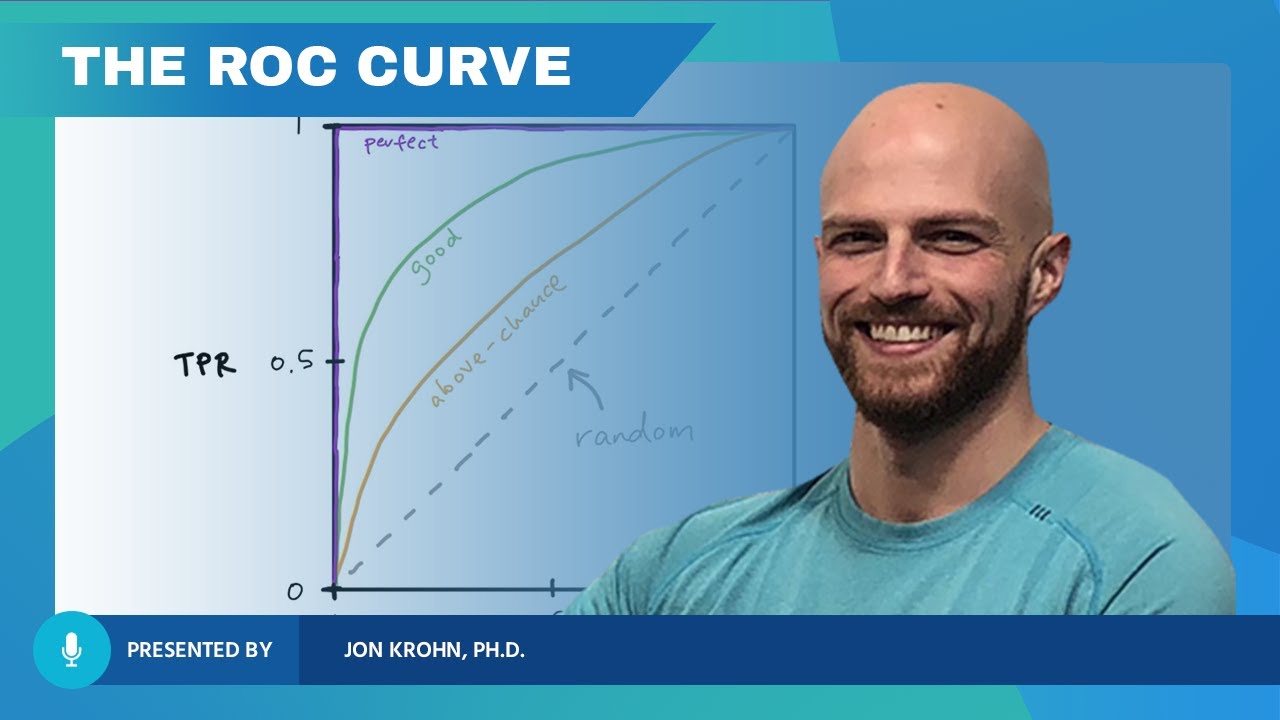
The ROC Curve (Receiver-Operating Characteristic Curve) — Topic 84 of Machine Learning Foundations

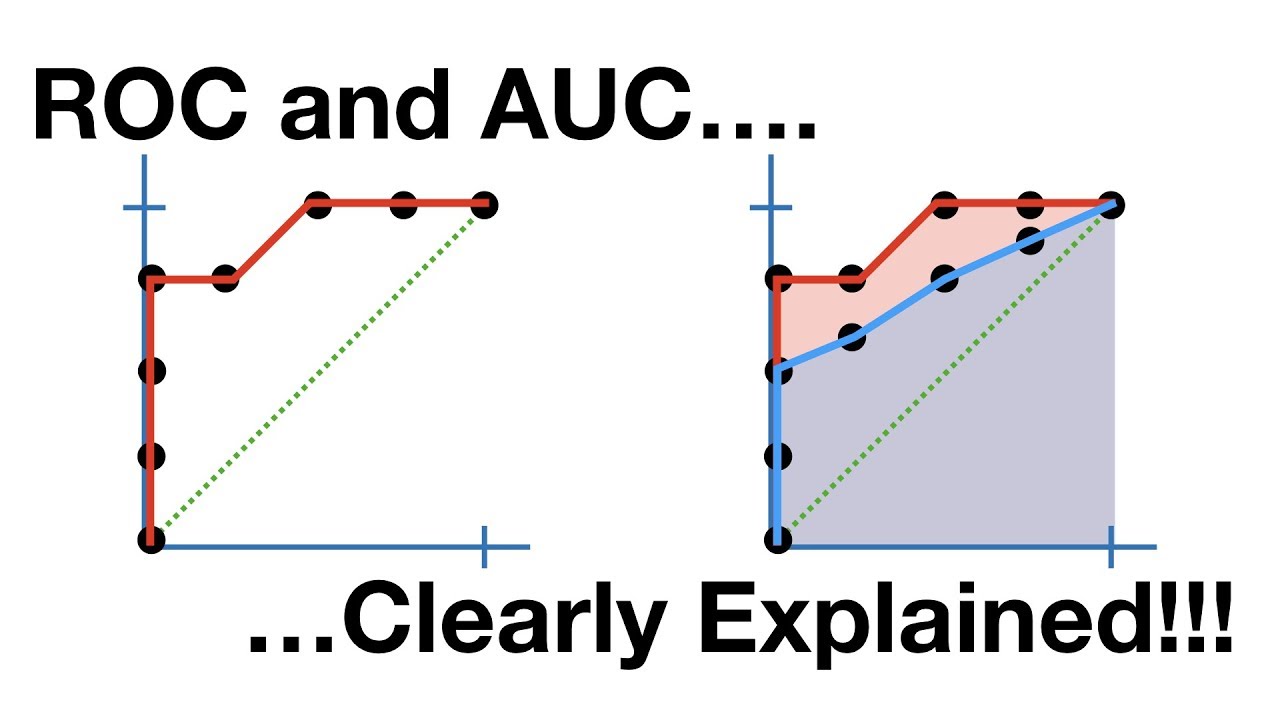
ROC and AUC, Clearly Explained!

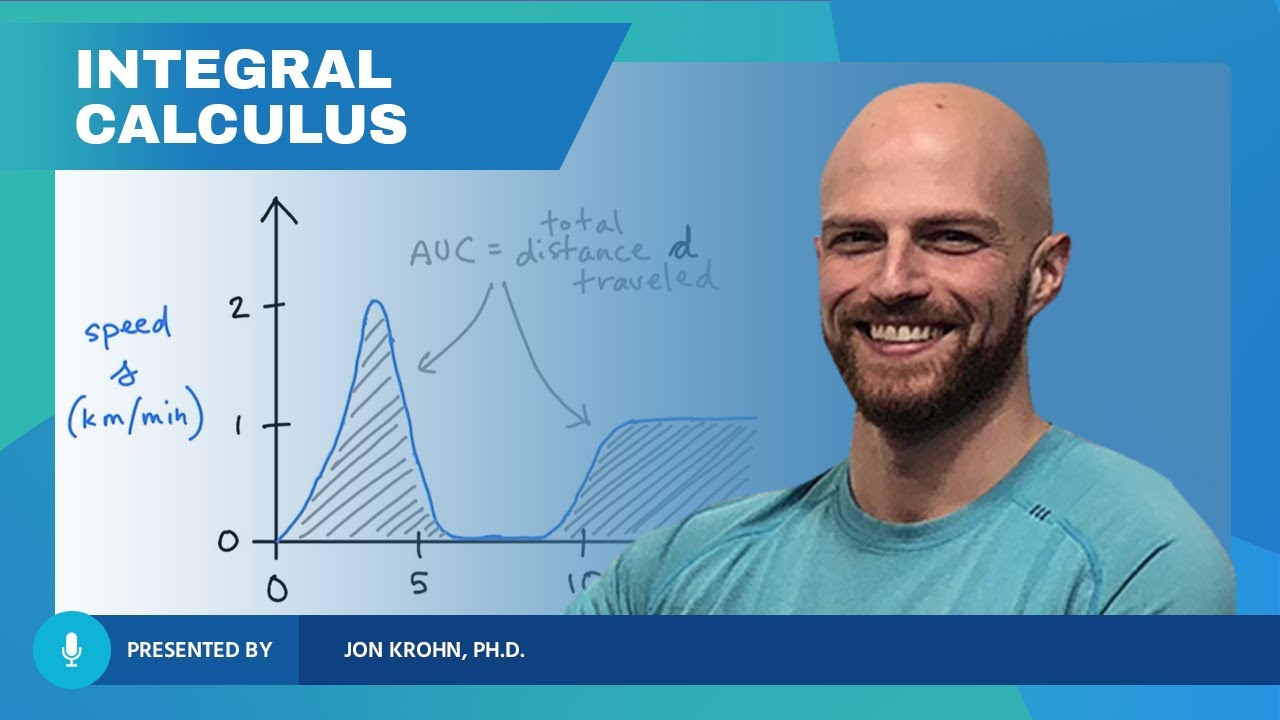
What Integral Calculus Is — Topic 85 of Machine Learning Foundations

ROC Curves

Calculus Applications – Topic 46 of Machine Learning Foundations

My Favorite Calculus Resources — Topic 92 of Machine Learning Foundations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Machine LearningIntegral CalculusPython CodingROC CurveAUC MethodTrapezoidal RuleScikit-LearnBinary ClassificationModel AssessmentNumerical ApproachData Science