Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 3)
TLDRThis video script is a comprehensive guide for students preparing for the AP Calculus BC exam, focusing on polar parametric vector multiple-choice questions. The instructor walks through various problems, emphasizing the importance of understanding the fundamental theorem of calculus and its application to find instantaneous rates of change, velocity vectors, and the area of regions bounded by polar curves. The script also covers the calculation of derivatives in parametric equations and the use of the chain rule and product rule in polar coordinates. The instructor provides step-by-step solutions, highlighting common mistakes to avoid and offering tips for solving problems efficiently. The video is designed to help students become adept at recognizing patterns and applying the right techniques, preparing them for the rigor of the AP exam.
Takeaways
- 📚 The video is a practice session for AP Calculus BC exam, focusing on polar parametric vector multiple-choice questions, which are also beneficial for general Calc 2 classes.
- 🧮 The presenter discusses the use of a calculator for solving integrals and derivatives, emphasizing the importance of understanding the fundamental theorem of calculus.
- 📈 The instantaneous rate of change of a vector function is calculated using the derivative, and the presenter shows how to rearrange the fundamental theorem to find the function's value at a different point.
- 🔄 The concept of velocity and position in vector calculus are explained, with the velocity vector being the derivative of the position vector.
- ∫ The method for finding the area of a region bounded by a polar curve involves integrating the squared radial function over the given interval.
- 📉 The process of finding the second derivative of y with respect to x for a given polar curve is demonstrated, highlighting the need to understand the relationship between dx/dθ and dy/dθ.
- 🏃 The speed of an object moving in the xy-plane, given by parametric equations, is found by taking the square root of the sum of the squares of its derivatives.
- 🤔 The importance of understanding the bounds of integration when dealing with polar graphs is stressed, as it is crucial for calculating areas and volumes.
- 📐 The video explains how to find the slope of a tangent line to a polar curve by using derivatives and the relationship between dy/dx and dx/dy.
- 🚀 The application of the fundamental theorem of calculus is shown in various contexts, including finding the position of a particle and the slope of a tangent line.
- 🔢 The presenter emphasizes the need for careful calculation and the avoidance of common mistakes, such as confusing variables or misapplying the chain rule.
- ✅ The video concludes with a reminder to practice and master all types of problems, as repetitive practice is key to readiness for the AP exam.
Q & A
What is the main topic of the video?
-The video is focused on practicing polar parametric vector multiple choice questions for the AP Calculus BC exam, which is also useful for any Calculus 2 class.
What is the significance of the vector valued function g(t) in the first problem?
-The vector valued function g(t) represents the position of an object, and its instantaneous rate of change is given by r(t). The problem involves finding the value of g at t=0 using the fundamental theorem of calculus.
How does the instructor approach finding the second derivative of y with respect to x for a polar curve?
-The instructor uses the given dx/dθ and dy/dθ to find dy/dx, and then finds the second derivative by differentiating dy/dx with respect to θ, and finally evaluates it at the given value.
What is the concept of 'speed' in the context of the parametric equations for an object moving in the xy-plane?
-The speed of the object is the magnitude of its velocity, which is calculated as the square root of the sum of the squares of dx/dt and dy/dt.
How does the instructor determine the area of the region bounded by a polar curve?
-The instructor uses the bounds provided and integrates half the square of the given polar function with respect to θ over the interval, which simplifies the integration process.
What is the importance of understanding the relationship between rectangular and polar graphs?
-Understanding the relationship between rectangular and polar graphs is crucial for solving calculus problems involving polar coordinates, as it helps in visualizing and setting up the integrals correctly.
How does the instructor approach finding the velocity vector of a particle given its parametric equations?
-The instructor finds the derivatives dx/dt and dy/dt, and then uses these to determine the velocity vector v(t) = (dx/dt, dy/dt) at the specified parameter value.
What is the key to solving the problem involving the vector-valued function f(t) and finding f at negative 1?
-The key is to rearrange the fundamental theorem of calculus to solve for the position at negative 1, by subtracting the integral of the velocity function from the known position at 1.
How does the slope of the tangent line to a polar curve relate to the derivatives dx/dθ and dy/dθ?
-The slope of the tangent line to a polar curve is found by dividing dy/dθ by dx/dθ, which gives the change in y over the change in x at a particular point on the curve.
What is the common mistake to avoid when finding dy/dx for parametric equations?
-The common mistake to avoid is confusing the parameter t with the variable x or y. It is important to differentiate with respect to t and solve for dy/dx carefully.
How does the instructor determine the equation of the tangent line to a curve described by parametric equations?
-The instructor finds the derivative dy/dx by differentiating y with respect to t and dividing by the derivative of x with respect to t. Then, using the point on the curve determined by t, the instructor uses the point-slope form to find the equation of the tangent line.
Outlines
📚 AP Calculus BC Exam Preparation
This video is part of a series aimed at practicing polar parametric vector multiple-choice questions for the AP Calculus BC exam. The content is also beneficial for any Calc 2 class. The presenter has completed problems for eight parts, with the first two already available and the rest to be completed soon. The video focuses on a calculator-based question involving the instantaneous rate of change of a vector function and utilizes the fundamental theorem of calculus to find the solution. The presenter also discusses the peculiarity of the function notation and provides a step-by-step approach to solving the problem, emphasizing the importance of rearranging the theorem to fit the question's requirements.
📏 Calculating Speed and Arc Length
The second paragraph deals with calculating the speed of an object moving in the x-y plane, given by parametric equations. The concept of speed as the magnitude of velocity is introduced, and the formula for speed is derived using the derivatives of the parametric equations. The presenter demonstrates how to use a calculator to find the speed and touches upon the concept of arc length as the integral of speed. The video then moves on to finding the area of a region bounded by a polar curve, emphasizing the importance of understanding the bounds of integration and the relationship between rectangular and polar graphs.
🔍 Derivatives and Area Calculations in Polar Coordinates
The third paragraph continues the theme of calculus with a focus on derivatives and area calculations in polar coordinates. The presenter discusses the process of finding the second derivative of y with respect to x for a given polar curve, highlighting the need to understand the relationship between dy/dx and dx/dt. The method for calculating the area of regions bounded by polar equations is also covered, with the presenter pointing out common mistakes in the provided answer choices and demonstrating the correct approach to finding the area.
🚀 Vector-Valued Functions and Tangent Line Equations
The fourth paragraph delves into vector-valued functions and the calculation of velocity vectors. The presenter explains how to find the velocity vector given a set of parametric equations and emphasizes the importance of differentiating correctly with respect to the parameter t. The video also covers finding the instantaneous rate of change of a vector function and using the fundamental theorem of calculus to solve for the function's value at a specific point. The process of finding the slope of a tangent line to a polar curve and the equation of a tangent line to a curve defined by parametric equations are also discussed, with the presenter cautioning against common mistakes such as confusing the parameter with the variable.
🧮 Implicit Differentiation and Solving for dy/dx
The final paragraph of the script addresses an unconventional problem involving implicit differentiation. The presenter is tasked with finding dy/dx for a curve defined by parametric functions where a relationship between x(t) and y(t) is given. The solution involves differentiating both sides of the given equation with respect to t and rearranging to solve for dy/dx. The video concludes with a reminder of the importance of understanding various problem types and the presenter's intention to continue the series in subsequent videos.
Mindmap
Keywords
💡Polar Parametric Vector
💡Instantaneous Rate of Change
💡Fundamental Theorem of Calculus
💡Derivative
💡Integral
💡Vector-Valued Function
💡Parametric Equations
💡Speed and Velocity
💡Area Calculation
💡Tangent Line
💡Chain Rule
Highlights
The video provides practice for AP Calculus BC exam with a focus on polar parametric vector multiple choice questions.
The video is part three of an eight-part series, covering various calculus topics.
The presenter uses the fundamental theorem of calculus to solve for the instantaneous rate of change of a vector-valued function.
A typo in the function notation is acknowledged, but the presenter rearranges the theorem to find the solution.
The x and y coordinates are calculated using integral calculus to find the value of g at zero.
The presenter emphasizes the importance of understanding the relationship between rectangular and polar graphs for calculus problems.
The area of a region bounded by a polar curve is calculated using a definite integral.
The bounds of integration are determined by analyzing the graph and the period of the polar function.
The video demonstrates how to find the speed of an object given parametric equations for its position.
The magnitude of velocity is used to calculate speed, which is a common concept in physics and calculus.
The area of a region in the first quadrant bounded by a polar curve is found using an integral that eliminates the square root.
The presenter advises on the strategy of looking at answer choices to identify common mistakes and find the likely correct answer.
The velocity vector of a particle is determined using derivatives of parametric equations.
The concept of the fundamental theorem is applied to find the position of a vector-valued function at a specific point in time.
The slope of a tangent line to a polar curve is calculated using derivatives and the unit circle.
The video covers the common mistake of confusing variables in parametric equations and emphasizes the importance of clarity.
An equation of a tangent line to a curve defined by parametric functions is derived using point-slope form and algebraic manipulation.
The video concludes with an unusual problem involving implicit differentiation to find the derivative of y with respect to x.
Transcripts
Browse More Related Video

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 2)

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 4)
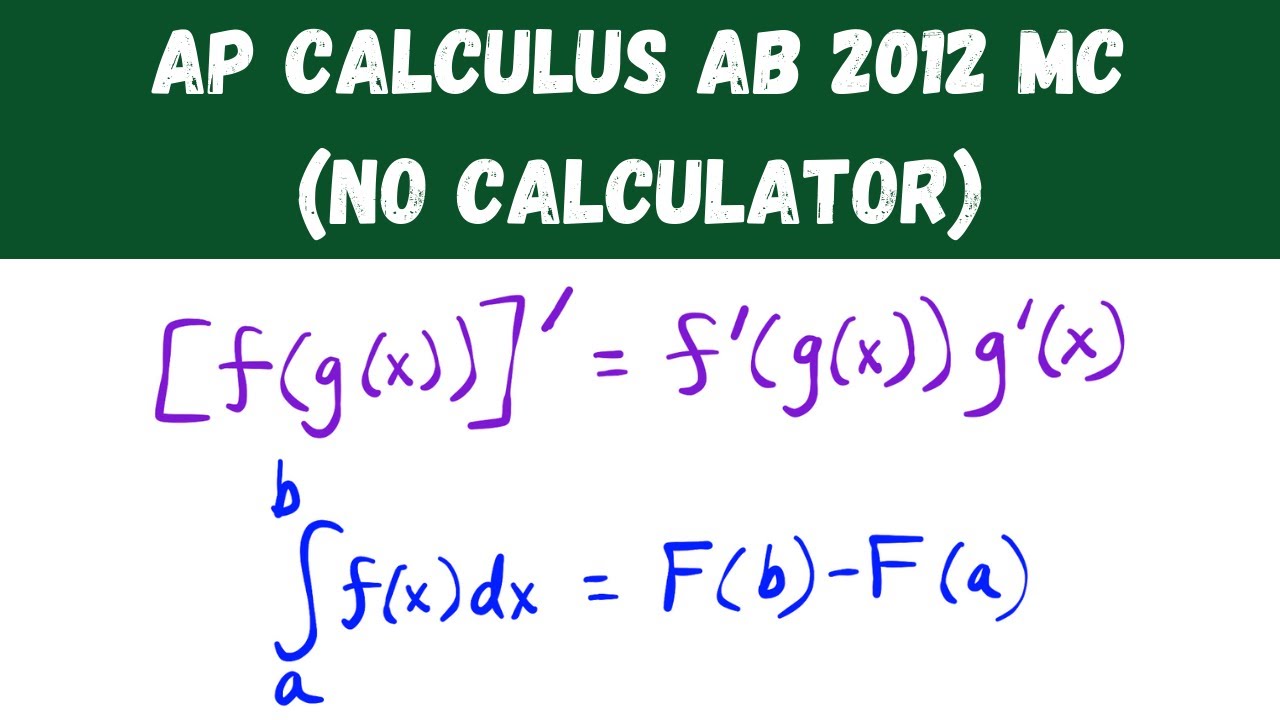
AP Calculus AB 2012 Multiple Choice (no calculator) - Questions 1-28

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 1)
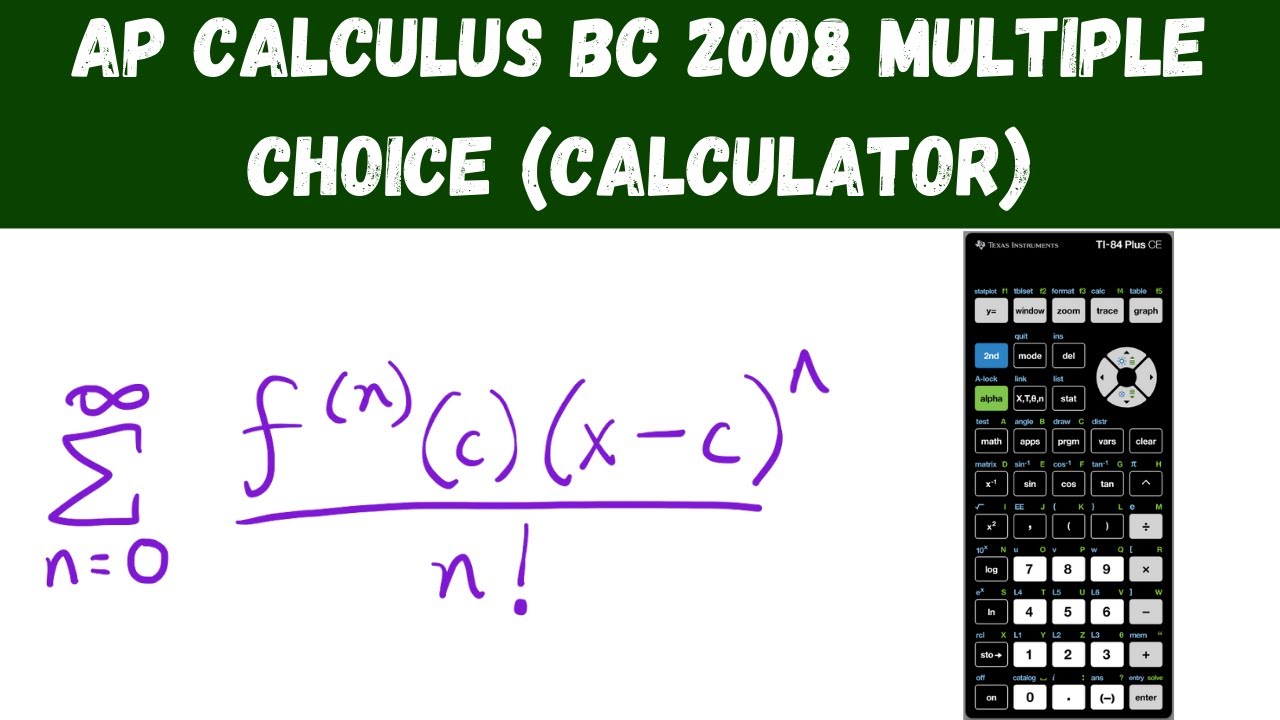
AP Calculus BC 2008 Multiple Choice (calculator) - Questions 76 - 92

Calculus of Polar Curves: Distance Between Curves
5.0 / 5 (0 votes)
Thanks for rating: