Applications of Integration - AP Calculus Unit 8 Review
TLDRThis video concludes the AP Calculus review series by delving into the applications of integration. The presenter explains the concept of the average value of a function, which is a numerical representation of the central tendency of the function's values over an interval. The formula for calculating this is provided, highlighting the use of the integral and the fundamental theorem of calculus. The video then explores finding the area between two curves by subtracting the integrals of the respective functions. The presenter also covers methods for calculating volumes using integrals, including the disk method, washer method, and cross-sectional methods for various shapes like squares, equilateral triangles, and semi-circles. Each method is contextualized with an explanation of when and how to apply it. The video is aimed at providing foundational knowledge for AP Calculus students, ensuring they are well-prepared for their exams.
Takeaways
- 😀 Average value of a function is found using the formula: 1/(b-a) * integral from a to b of f(x) dx.
- 😎 The area between two curves can be found by subtracting the integral of the bottom curve from the integral of the top curve within the given interval.
- 🤔 When dealing with functions that intersect, convert them into functions of y and subtract the right function from the left to find the area between them.
- 😲 Volume can be calculated using the disk method by integrating pi * (f(x))^2 from a to b when rotating around the x-axis.
- 😯 For rotating shapes with holes (washer method), find the volume by integrating pi * (f(x) - g(x))^2 from a to b, where f(x) is the outer curve and g(x) is the inner curve.
- 😉 When using cross sections to find volume, integrate the area function (f(x) - g(x))^2 dx from a to b, considering different shapes like squares, equilateral triangles, or semicircles.
- 🧐 Remember to adjust formulas when dealing with different shapes and dimensions, such as halving the diameter for semi-circles.
- 📏 Make sure to correctly convert functions into appropriate forms when dealing with integrals and cross sections, depending on the axis of rotation.
- 🖩 Graphing calculators can aid in solving complex problems, especially when dealing with multiple functions and intervals.
- 👋 Concluding the AP Calculus review series, understanding these concepts is crucial for success in calculus and further mathematical studies.
Q & A
What is the average value of a function in calculus?
-The average value of a function in calculus is a numerical value that represents the mean or midpoint of the function's values over a given interval. It is calculated using the formula: ∫[a, b] f(x) dx / (b - a), where 'f(x)' is the function, and 'a' and 'b' are the endpoints of the interval.
How is the average value of a function different from the average rate of change?
-The average value of a function is the mean of all the function's values over an interval, while the average rate of change is the change in the function's value divided by the change in the independent variable (x) over the interval. The average rate of change is instantaneous at a point, whereas the average value is a global measure over the entire interval.
What is the formula for finding the area between two curves?
-The formula for finding the area between two curves is ∫[a, b] (f(x) - g(x)) dx, where 'f(x)' is the function representing the top curve, 'g(x)' is the function for the bottom curve, and 'a' and 'b' are the endpoints of the interval.
How do you determine which function is the top and which is the bottom when finding the area between two curves?
-To determine the top and bottom functions, you typically plot the functions on the same graph. The top function is the one that is above the x-axis when the bottom function crosses it. If the functions cross each other, you may need to break the integral into parts or express the functions in terms of y to determine the correct order.
What is the disc method for finding the volume of a solid of revolution?
-The disc method for finding the volume of a solid of revolution involves revolving a region around an axis to create a three-dimensional shape. The volume is found by integrating the area of each circular cross-section (pi * (f(x))^2) over the interval from 'a' to 'b', where 'f(x)' is the radius function and 'a' and 'b' are the limits of integration.
How does the washer method differ from the disc method in finding the volume of a solid of revolution?
-The washer method is used when the solid of revolution has a hole in the middle, like a ring. It involves subtracting the area of the inner circle (with radius 'g(x)') from the area of the outer circle (with radius 'f(x)') at each cross-section. The volume is then found by integrating pi * (f(x)^2 - g(x)^2) over the interval from 'a' to 'b'.
What is the formula for calculating the volume using the cross-sectional method with square cross-sections?
-The formula for calculating the volume using the cross-sectional method with square cross-sections is ∫[a, b] (f(x) - g(x))^2 dx, where 'f(x)' and 'g(x)' are the lengths of the sides of the squares, and 'a' and 'b' are the limits of integration.
How do you find the volume of a solid of revolution with equilateral triangular cross-sections?
-The volume of a solid of revolution with equilateral triangular cross-sections is found by integrating the area of one triangle, which is (sqrt(3)/4) * side^2, over the interval from 'a' to 'b'. The formula is ∫[a, b] (sqrt(3)/4) * (f(x) - g(x))^2 dx, where 'f(x)' and 'g(x)' are the lengths of the sides of the triangles.
What is the formula for calculating the volume of a solid of revolution with semicircular cross-sections?
-The formula for calculating the volume of a solid of revolution with semicircular cross-sections is ∫[a, b] (pi/2) * ((f(x) - g(x))/2)^2 dx, where 'f(x)' and 'g(x)' are the diameters of the semicircles, and 'a' and 'b' are the limits of integration.
Why is it important to graph functions when finding the area between two curves or the volume of a solid of revolution?
-Graphing functions is important because it helps visualize the shape of the region of interest and clarify which function is above or below at any given point. It also helps in determining the correct limits of integration and the order of functions for subtraction when calculating areas or volumes.
How does the choice of axis for rotation affect the formula used in the disc or washer method?
-The choice of axis for rotation affects whether you use 'x' or 'y' as the variable in the formula. If the region is revolved around the x-axis, the radius is a function of 'x', and if revolved around the y-axis, the radius is a function of 'y'. This requires converting the function from 'f(x)' to 'f(y)' when necessary.
Outlines
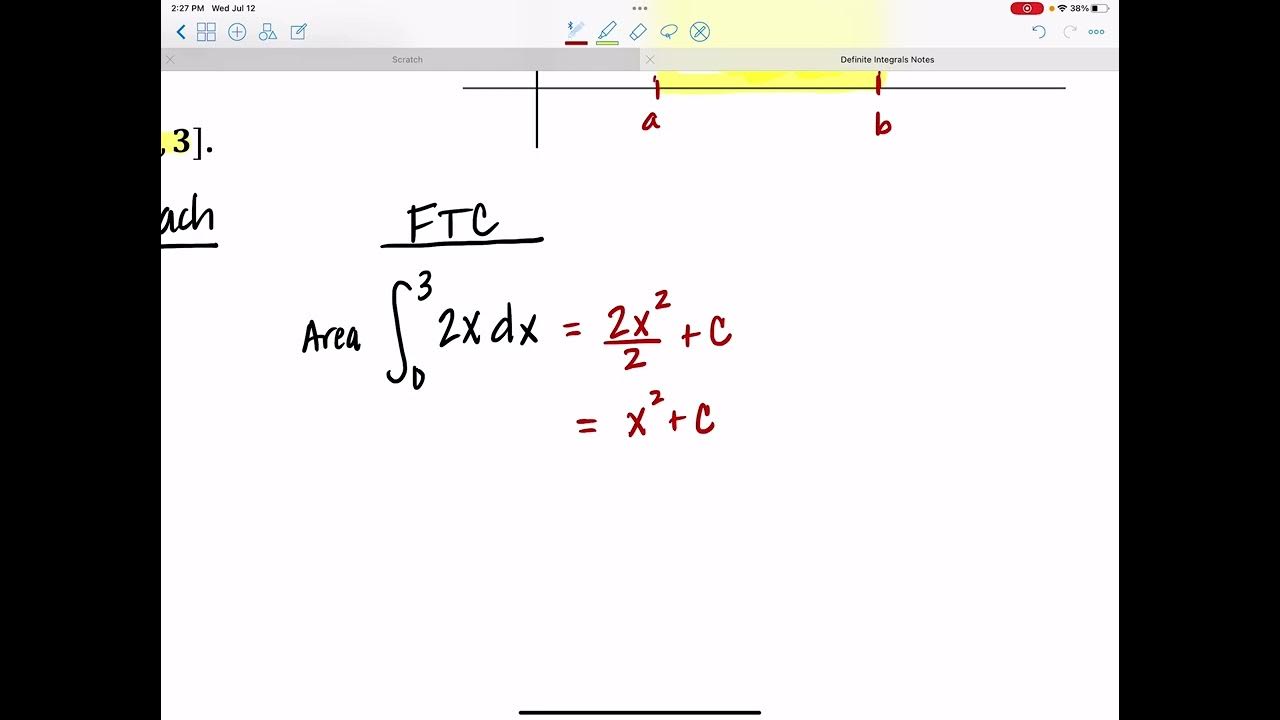
📊 Understanding Average Value of a Function
The first paragraph introduces the concept of the average value of a function, which is a key topic in AP Calculus Unit 8. It distinguishes between average rate of change and average value, with the latter being the focus. The average value is calculated by summing all the y-values of a function over an interval and dividing by the length of the interval. The formula provided is \( \bar{f} = \frac{1}{b-a} \int_{a}^{b} f(x) \, dx \), which can be simplified using the Fundamental Theorem of Calculus to \( \frac{F(b) - F(a)}{b-a} \), where \( F(x) \) is the antiderivative of \( f(x) \). The explanation includes the idea of averaging the values of a function over an interval to find a single representative value, which is akin to the average rate of change but over an infinite number of points.
📈 Area Between Two Curves
The second paragraph explains how to calculate the area between two curves, which is a common application of integration. The method involves finding the integral from a to b of the difference between the two functions, \( f(x) \) and \( g(x) \), where \( f(x) \) is the function representing the top curve and \( g(x) \) the bottom curve. The formula for this calculation is \( \int_{a}^{b} (f(x) - g(x)) \, dx \). The paragraph also discusses the importance of graphing the functions to visualize the area and the potential need to convert functions into the appropriate form, such as functions of y, depending on the orientation of the curves with respect to the axes.
🔄 Disk and Washer Methods for Volume
The third paragraph delves into the disk and washer methods for finding the volume of solid objects generated by revolving a region around an axis. The disk method is used when the cross-sectional area is a circle, with the formula \( \pi \int_{a}^{b} [f(x)]^2 \, dx \), where \( f(x) \) is the radius as a function of x. If the object has a hole in the middle, the washer method is more appropriate, which involves subtracting the area of the smaller circle from the larger one, resulting in the formula \( \pi \int_{a}^{b} [f(x) - g(x)]^2 \, dx \). The paragraph emphasizes the need to adjust the method based on whether the rotation is around the x-axis or y-axis and to ensure that all calculations are done with the correct variable.
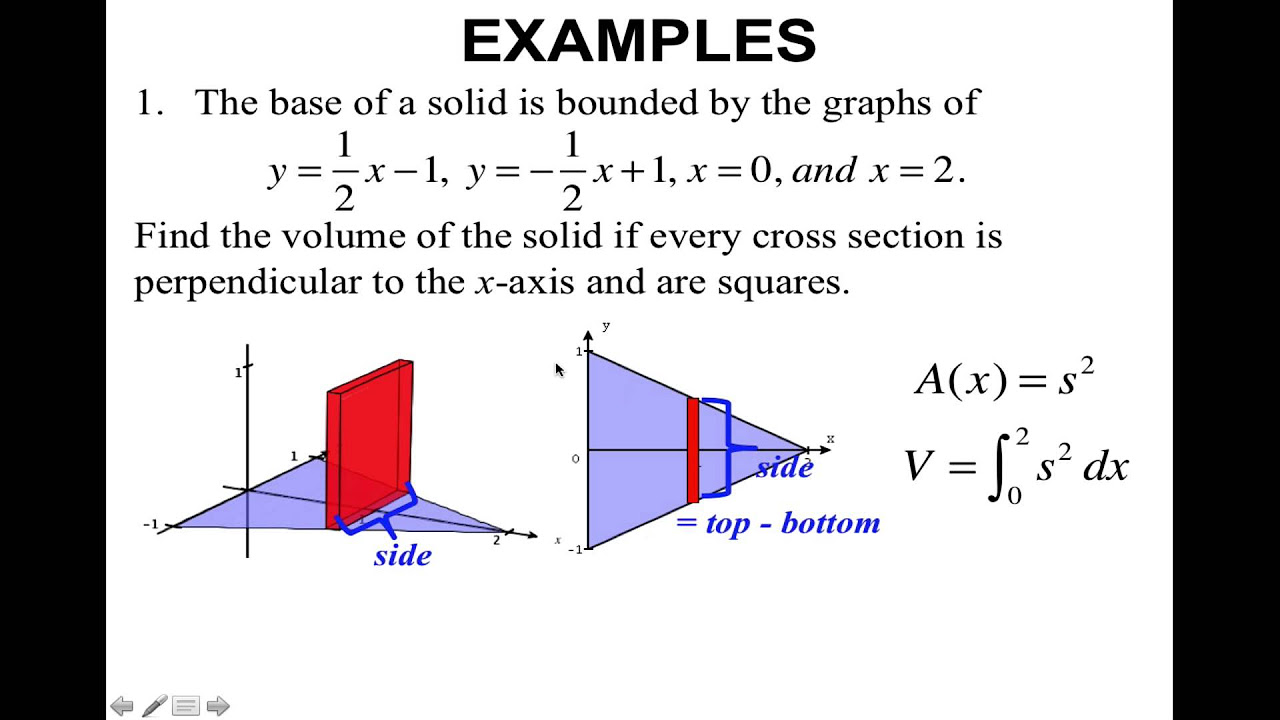
🏗 Cross-Sections and Volume Calculations
The fourth paragraph continues the discussion on calculating volumes with integration, focusing on cross-sections that are not circular. It introduces the concept of integrating the area of various geometric shapes to find the volume. The method involves finding the area of a single cross-section and then integrating over the interval to find the total volume. Examples given include squares, equilateral triangles, and semi-circles, each with their specific area formulas. The paragraph emphasizes the importance of correctly identifying the length of the cross-section, which is the difference between the two function values, and then squaring this value to find the area of the cross-section.
🎓 Conclusion of AP Calculus Review Series
The final paragraph concludes the AP Calculus review series, summarizing the methods for finding volumes using integration, including the disk, washer, and cross-section methods. It encourages the use of graphing calculators to assist with complex problems and expresses gratitude to the viewers for their engagement throughout the series. The presenter also hints at making a future video to explain the derivation of the area formula for an equilateral triangle.
Mindmap
Keywords
💡Average Value of a Function
💡Integral
💡Fundamental Theorem of Calculus
💡Area Between Two Curves
💡Disk Method
💡Washer Method
💡Cross-Sections
💡Volume
💡Equilateral Triangle
💡Semi-Circle
💡Graphing Calculator
Highlights
The video discusses the average value of a function, a concept distinct from the average rate of change.
The average value is calculated by integrating the function over an interval and dividing by the length of the interval.
The formula for average value is given as the integral from 'a' to 'b' of f(x) dx, divided by (b - a).
The concept of the area between two curves is introduced, which involves subtracting the integral of one function from another over a common interval.
The method for finding the area between curves can be visualized by graphing and is essential for understanding volume calculations.
When dealing with multiple curves, it's important to identify which function represents the top and bottom curves for the area calculation.
The disc method for finding volume involves rotating a region around the x-axis and calculating the volume of the resulting solid.
The volume of a solid of revolution obtained using the disc method is given by π times the integral from 'a' to 'b' of [f(x)]^2 dx.
The washer method is used when there's a hole in the middle of the region being revolved around an axis.
The volume calculation for a washer is the integral from 'a' to 'b' of π times [f(x) - g(x)]^2 dx, where f(x) is the outer radius and g(x) is the inner radius.
Cross-sections that are not circular, such as squares or equilateral triangles, require different area formulas to calculate volume.
For a cross-section in the shape of a square, the volume is found by integrating the length of the sides squared, (f(x) - g(x))^2, over the interval.
An equilateral triangle cross-section requires the area formula (root 3/4) times side^2, leading to an integral of (root 3/4) times [f(x) - g(x)]^2 dx for volume.
For a semicircular cross-section, the volume is calculated by integrating pi/2 times [(f(x) - g(x))/2]^2 dx over the interval.
The video emphasizes the importance of correctly identifying the limits of integration (a and b) and ensuring that all expressions are in terms of the correct variable, x or y.
The video concludes the AP Calculus review series, summarizing key concepts and methods for finding volumes and areas in calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: