AP Calc AB & BC Practice MC Review Problems #2

turksvids

11 Jan 202024:22

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers a comprehensive review of multiple-choice calculus problems, presumably for the AP exam. The presenter begins by addressing the first question, which involves calculating integrals and recognizing potential pitfalls in the problem's phrasing. The discussion then transitions into tackling a variety of calculus problems, including evaluating limits, applying implicit differentiation, and interpreting the graph of a function's second derivative. The script emphasizes the importance of understanding and correctly applying fundamental calculus concepts such as u-substitution, the limit definition of the derivative, and the properties of logarithms. Each problem is methodically solved, highlighting the step-by-step process and the mathematical reasoning behind it. The video concludes with a problem involving a piecewise function and its corresponding integral, reinforcing the application of the Fundamental Theorem of Calculus. Throughout the script, the presenter encourages viewers to practice and verify their understanding of the material, ensuring they are well-prepared for the rigors of the AP exam.

Takeaways

📚 The video is a review session covering multiple-choice calculus problems based on previous AP exams.
🔍 The presenter emphasizes the importance of trying out the problems before watching the video to check solutions.
✅ The first problem involves calculating integrals and using the properties of integrals to find the value of an integral over a different interval.
📈 The second problem is about finding the equation of the tangent line to a function at a specific point using point-slope form.
🤔 The third problem deals with setting up compound inequalities based on the areas under a curve represented by integrals.
👉 The fourth problem is a u-substitution technique application to evaluate a definite integral.
🚀 The fifth problem involves implicit differentiation to find the derivative of a relationship between x and y at a given point.
📉 The sixth problem is about integrating acceleration to find velocity and then position of a particle over time.
🔢 The seventh problem requires determining which graph could represent a function based on the graph of its second derivative.
🎓 The eighth problem is a limit definition of the derivative calculation, which involves properties of logarithms.
🔧 The ninth problem involves finding the fourth derivative of a given function and evaluating it at a specific point.
🧩 The final problem is an application of the fundamental theorem of calculus to find the integral of a piecewise function over an interval.

Q & A

What is the integral from 5 to negative 3 of f(x) dx, according to the video?
-The integral from 5 to negative 3 of f(x) dx is -6, as the bounds should be switched to reflect the negative value.
How does the video suggest to approach solving the integral from 5 to 8 of F(t) dt?
-The video suggests creating a bar graph to visualize the bounds and known integral values, then using these to deduce the unknown integral by subtracting the known integrals from one another.
What is the correct approach when dealing with an integral of the form F(2x) dx?
-The video demonstrates using a u-substitution where u = 2x, which leads to 1/2 du = dx, and then solving the integral in terms of u before substituting back.
How does the video find the equation of the tangent line to the graph of f at the point (e^2, 2ln3)?
-The video substitutes the point into the function f(x) to find the y-coordinate, then calculates the derivative f'(x) and evaluates it at the given x-coordinate. The point-slope form of the equation is then used with the found slope and point.
What is the strategy for ordering the given integrals from least to greatest?
-The video suggests estimating the areas under the curve for each integral's interval and then ordering these areas to determine the order of the integrals.
How does the video solve the integral from 1 to 2 of (2 times the quantity 3x to the 4th plus 1 to the 1/2 times x cubed) dx?
-The video uses u-substitution with u being the expression in parentheses, and then evaluates the new integral with the new bounds and solves it using basic integration techniques.
What is the method used in the video to find dy/dx if 2x^2 - 3xy + 4y^2 = 9 at the point (-1, 1)?
-The video uses implicit differentiation to find dy/dx, taking the derivative of both sides of the equation with respect to x, and then solving for dy/dx.
How does the video find the position of a particle at time T, given its acceleration and initial conditions?
-The video first integrates the acceleration function to find the velocity function, then integrates the velocity function to find the position function, and finally uses the initial conditions to find the constant of integration.
What does the video suggest when trying to determine the graph of f(x) from the graph of f''(x)?
-The video suggests recognizing that f''(x) being quadratic implies that f(x) is quartic. It then eliminates options that do not match the concavity and degree of the function.
How does the video calculate the limit as h approaches zero of (e^(3(x+h)) - e^(3x))/h when x equals the natural log of 5?
-The video identifies this as a limit definition of the derivative and substitutes x with the natural log of 5, then applies properties of exponents and logarithms to simplify and solve the limit.
What is the final answer for the integral from negative 2 to 2 of the piecewise function f(x) dx?
-The video breaks the integral into three parts, one for each segment of the piecewise function, calculates each integral separately, and then sums the results to find the final answer of negative 4.

Outlines

00:00

🔢 Calculus Multiple-Choice Review Problems

The video starts with an introduction to multiple-choice calculus review problems based on AP exams. The presenter emphasizes the lack of answer choices and encourages viewers to attempt the problems before watching the solutions. The first problem involves calculating an integral, which requires switching bounds and using a bar graph approach to find the solution. The presenter also discusses a potential mistake with the integral of F of 2X, suggesting a u-substitution is needed. The problem is solved step by step, leading to the final answer of 24.

05:01

📈 Tangent Line Equation and Function Graph Analysis

The second paragraph covers finding the equation of a tangent line to a function at a specific point, using point-slope form. The presenter demonstrates the process of substituting given values into the function and its derivative to find the slope of the tangent line. The video also addresses a compound inequality problem, where the presenter uses a visual approach to estimate areas under the curve and solve the inequality. The problem-solving strategy involves creating a rough sketch and ordering the given integrals from least to greatest.

10:01

🏃 Particle Motion and Derivative Applications

In the third paragraph, the video tackles problems related to particle motion and implicit differentiation. The presenter starts with finding the velocity function from a given acceleration function using integration. Then, using the initial conditions, the position function is derived. The next problem involves implicit differentiation to find the derivative dy/dx for a given equation at a specific point. The presenter emphasizes the importance of remembering that the derivative of a constant is zero.

15:03

📌 Second Derivative and Function Concavity

The fourth paragraph focuses on using the second derivative to determine the concavity of a function and to identify its graph. The presenter explains how to interpret the second derivative graph to find points of inflection and intervals where the function is concave up or down. By recognizing that the second derivative is a quadratic function, the presenter deduces that the original function must be a quartic. The process of elimination helps in selecting the correct graph that matches the concavity conditions.

20:05

🧮 Limit Definition of Derivative and Logarithmic Properties

The video continues with a problem that involves the limit definition of the derivative, specifically finding the derivative of a function at a point where x equals the natural log of 5. The presenter uses logarithmic properties to simplify the expression and find the derivative. The video also briefly touches on the importance of reviewing the unit circle and the graphs of sine and cosine functions for the AP exam.

🧬 Higher-Order Derivatives and Piecewise Function Integration

The final paragraph deals with finding higher-order derivatives and integrating a piecewise function. The presenter calculates the fourth derivative of a given function and evaluates it at x equals negative two. Then, the video moves on to integrating a piecewise function over an interval from negative two to two. The interval is broken down into three parts to account for the different sections of the piecewise function, and the integral is computed for each part separately before summing them up for the final answer.

Mindmap

Keywords

💡Integral

An integral is a concept in calculus that represents the area under a curve defined by a function. In the video, integrals are used to solve various problems, such as finding the area under a curve between two points (negative 3 to 5) and to find the position of a particle at a given time.

💡Multiple-choice questions

Multiple-choice questions are a type of question that provides a set of possible answers from which the correct one is chosen. The video script discusses the use of multiple-choice questions in the context of AP exams, where the presenter reviews problems without answer choices, allowing viewers to solve them first.

💡Derivative

The derivative in calculus is a measure of how a function changes as its input changes. In the video, the presenter finds derivatives to determine the slope of a tangent line to a graph and to solve differential equations, such as finding the velocity and position of a particle.

💡U-substitution

U-substitution is a method used in calculus to simplify the process of integrating complicated expressions. The video demonstrates the use of U-substitution in solving an integral involving a term with X cubed, which is transformed into an integral in terms of U for easier computation.

💡Point-slope form

Point-slope form is a way of writing the equation of a line that passes through a given point and has a specific slope. The video uses point-slope form to find the equation of the line tangent to a function at a particular point, which is a common problem type in calculus.

💡Second derivative

The second derivative is the derivative of the first derivative of a function, which can indicate the concavity of a function's graph. In the video, the presenter uses the second derivative to determine the concavity and points of inflection of a function, which is crucial for understanding the function's behavior.

💡Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus connects differentiation and integration, stating that the definite integral of a function can be found by finding the antiderivative of the function and evaluating it at the limits of integration. The video uses this theorem to solve various integral problems throughout the script.

💡Concavity

Concavity refers to the curvature of a function's graph—whether it curves upward (concave up) or downward (concave down). The video discusses concavity in relation to the second derivative and uses it to determine the shape of a function's graph from its second derivative plot.

💡Chain rule

The chain rule is a method in calculus for finding the derivative of a composite function. It is used in the video when differentiating a function like e to the 3x and when finding the derivative of an implicit function, such as 2x squared minus 3xy plus 4y squared equals 9.

💡Piecewise function

A piecewise function is a function that is defined by multiple sub-functions, each applicable to a different interval or region. The video script includes a problem where the integral of a piecewise function is calculated by breaking it down into separate integrals for each sub-function.

💡Limit definition

The limit definition is a fundamental concept in calculus that describes the behavior of a function as its input approaches a certain value. The video script addresses the limit definition when finding the derivative of a function at a specific point, such as the derivative of e to the 3x at the natural log of 5.

Highlights

The video presents multiple-choice review problems based on previous AP exams, focusing on integral calculus.

The first problem involves calculating the integral from 5 to 8 of F of T DT, using given integral values.

A u-substitution technique is used to solve an integral involving 2 times the quantity 3x to the 4th plus 1 to the 1/2 times X cubed.

The video demonstrates the process of implicit differentiation to find dy/dx for a given equation at a specific point.

Integration of acceleration over time is shown to find the position of a particle at time T, given initial velocity and position.

The use of the second derivative to determine the concavity and inflection points of a function is explained.

A limit definition of the derivative is used to find the derivative of e to the 3x at the natural log of 5.

The video covers the process of finding the fourth derivative of a given function and evaluating it at x equals negative two.

A piecewise function is integrated over the interval from negative 2 to 2 by breaking it into separate integrals for each piece.

The importance of understanding the fundamental theorem of calculus for solving integrals is emphasized.

The video provides a comprehensive review of integral calculus concepts applicable to AP exams.

The use of bar graphs to visualize and solve integral calculus problems is demonstrated.

The video explains how to rewrite an integral with a u-substitution to make it easier to solve.

The process of finding the equation of the tangent line to a graph at a given point is shown using point-slope form.

The video illustrates how to determine the area under a curve by approximating regions and summing their values.

The concept of integrating a function to find velocity and then integrating velocity to find position is covered.

The video discusses how to identify the graph of a function based on the graph of its second derivative and the function's degree.

The application of properties of logarithms is shown in finding the derivative of a function at a specific point.

The final problem involves integrating a piecewise function over a specified interval, demonstrating the handling of discontinuities.

Transcripts

Browse More Related Video

AP Calculus BC 2008 Multiple Choice (no calculator) - questions 1 - 28

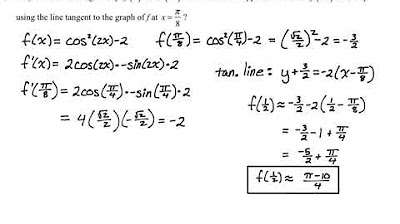
AP Calc AB & BC Practice MC Review Problems #4

AP Calculus AB 2003 Multiple Choice (no calculator) - Questions 1-28

AP Calculus AB 2008 Multiple Choice (Calculator) - Questions 76-92

AP Calculus Multiple Choice Practice Test (2020 AP CED Problems)

AP Calculus AB 2012 Multiple Choice (calculator) - Questions 76 - 92

Related Tags

AP Calculus Multiple-Choice Integral Calculus Derivatives U-Substitution Point-Slope Form Concavity Piecewise Functions Logarithmic Differentiation Fundamental Theorem Educational Content