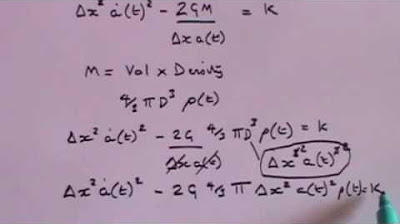Cosmology Lecture 5
TLDRThe provided script is a detailed lecture on the concepts of cosmology, focusing on the equation of state and its implications for the evolution of the universe. The lecturer discusses the importance of understanding the time history of the scale factor in the universe, which is central to answering the fundamental question of the universe's history. The matter dominated and radiation dominated models are reviewed, highlighting how they represent different evolutionary conditions characterized by specific equations of state. The lecturer further explores the relationship between pressure, energy density, and the scale factor, particularly emphasizing the role of the equation of state in cosmology. The script delves into the derivation of the equation of state for radiation, where pressure is proportional to the energy density, and introduces the concept of vacuum energy, or the cosmological constant, which has a constant energy density that does not change with the expansion of the universe. The lecture concludes with a discussion on the implications of vacuum energy for the expansion of the universe, including the potential for exponential growth in the case of a positive cosmological constant and the possibility of a 'big crunch' in the case of a negative cosmological constant. The lecturer also touches on the mystery of the cosmological constant's small value and its significance in the context of quantum field theory.
Takeaways
- 📚 The fundamental question in cosmology is understanding the history of the universe, which can be described by the time history of the scale factor.
- 🔍 In a homogeneous and isotropic universe, the scale factor's evolution is crucial for understanding the universe's history and can be tested and observed through various means.
- 🌌 Two primary models studied are the matter-dominated model, where the scale factor expands like t^(2/3), and the radiation-dominated model, expanding like t^(1/2).
- 🚀 The importance of the equation of state lies in its ability to describe how the energy density changes with the scale factor, which is vital for understanding the universe's evolution.
- 🔑 The equation of state is characterized by 'w', a number that relates the pressure to the energy density (pressure = w * energy density) and is key to distinguishing different types of cosmological fluids.
- ✨ For non-relativistic matter, the pressure is approximately zero compared to the energy density, which corresponds to w = 0, indicating a matter-dominated universe.
- 🌟 In a radiation-dominated universe, w equals 1/3, leading to the energy density scaling with the scale factor to the power of 4, as derived from the equation of state for radiation.
- ⚖️ The concept of vacuum energy, or dark energy, is introduced as a form of energy density inherent in empty space, with a constant energy density that does not change with the expansion of the universe.
- ⏱️ The vacuum energy density has an equation of state where w = -1, meaning that the pressure and energy density have opposite signs, leading to accelerated expansion of the universe.
- 🧵 The cosmological constant (Λ) is related to the vacuum energy density and is used in the Friedmann equations to describe the expansion rate of the universe.
- ⛔️ Negative pressure can occur and is associated with tension; an example given is a spring connecting two ends of a box, which pulls the walls in, representing negative pressure.
Q & A
What is the fundamental question in cosmology?
-The fundamental question in cosmology is understanding the history of the universe, particularly the time history of the scale factor, which provides a significant understanding of the universe's evolution.
What are the two models of universe expansion discussed in the script?
-The two models discussed are the matter dominated model, where the scale factor (a of t) expands like t to the two thirds, and the radiation dominated model, where it expands like t to the one half.
What is the equation of state in cosmology?
-In cosmology, the equation of state is a relationship that characterizes how the energy density changes with changes in the scale factor. It is often simplified to pressure being some number, denoted as 'w', times the energy density (rho).
How does the energy density scale with the scale factor in a matter dominated universe?
-In a matter dominated universe, the energy density (rho) is proportional to one over the scale factor cubed (a^-3), which means rho = rho_nought / a^3.
What is the equation of state for radiation?
-For radiation, the equation of state is given by w equals one third, which means pressure is equal to one third times the energy density (rho).
What is the significance of the cosmological constant (Lambda) in the context of vacuum energy?
-The cosmological constant (Lambda) represents the energy density of empty space, or vacuum energy. It is a constant value that does not change with the expansion of the universe and is associated with a negative pressure that can lead to an accelerated expansion of the universe.
What is the relationship between pressure and energy density for vacuum energy?
-For vacuum energy, the pressure is equal to the negative of the energy density. This means that if the energy density is positive, the pressure is negative, and vice versa, which is represented by w = -1.
What is the Sitter space?
-The Sitter space is a solution of Einstein's equations with a positive cosmological constant, where the universe exponentially expands. It is named after the Dutch physicist and astronomer Willem de Sitter.
What are the implications of a positive vacuum energy density in the universe?
-A positive vacuum energy density can lead to an exponential expansion of the universe, which is observed as an accelerated expansion. This is a key component of the current understanding of the universe's expansion history.
What is the role of the cosmological constant in the Friedmann equations?
-The cosmological constant (Lambda) appears in the Friedmann equations as a term that contributes to the expansion dynamics of the universe. It is particularly important in describing the late-time acceleration of the universe's expansion.
What is the current observational evidence regarding the value of w (the equation of state parameter for vacuum energy)?
-Current observational evidence suggests that w is close to -1, indicating that the energy density of the universe behaves like vacuum energy. The precision measurements are narrowing down the value of w, which is consistent with the idea of dark energy driving the accelerated expansion of the universe.
Outlines
🌌 Cosmology and the Equation of State
The paragraph introduces the topic of cosmology, focusing on the equation of state and its importance in understanding the universe's history. It emphasizes the scale factor's time history and how different宇宙学 models, like the matter dominated and radiation dominated models, contribute to our knowledge of the cosmos. The discussion also touches on the role of the equation of state in characterizing the energy density's change with the scale factor.
📐 The Equation of State and Its Simplifying Assumptions
This section delves into the equation of state, assuming a simplified relationship between pressure and energy density. It uses the parameter 'w' to characterize different types of matter or energy in the universe, such as non-relativistic matter (w=0) and radiation (w=1/3). The paragraph also explains how the energy density depends on the scale factor through the equation of state.
🔄 Work-Energy Principle in a Cosmological Context
The paragraph explores the work-energy principle within the context of cosmology. It discusses how the energy inside a hypothetical box changes as the box expands, relating this to the work done by the gas inside the box. The summary includes the derivation of the relationship between energy density and the scale factor, leading to a famous equation in cosmology.
📉 Energy Density and the Scale Factor
This part of the script focuses on the relationship between energy density and the scale factor. It derives the famous equation that energy density is proportional to the inverse of the volume to the power of (1+w). The summary explains how this formula is applied to both matter dominated and radiation dominated scenarios, leading to different evolutions of the universe.
💡 Derivation of the Equation of State for Radiation
The paragraph provides a detailed derivation of the equation of state for radiation, considering a box filled with photons. It discusses the characteristics of photons, such as their energy and momentum, and how these properties lead to the equation of state for radiation, where w equals one third.
🚀 Momentum and the Number Density of Photons
This section calculates the pressure exerted by photons in a box, considering their number density and the momentum of individual photons. The summary explains the process of calculating the force on the box's walls due to photons and how this leads to the understanding of radiation pressure.
🤔 The Cosmological Constant and Vacuum Energy
The paragraph introduces the concept of vacuum energy and the cosmological constant. It discusses how vacuum energy is a form of energy density that exists in empty space and is characterized by a constant value. The summary also touches on the implications of vacuum energy in the context of the Friedmann equations and the expansion of the universe.
🌟 The Role of Vacuum Energy in the Universe's Expansion
This part discusses the role of vacuum energy in the universe's expansion, highlighting that vacuum energy density corresponds to a cosmological constant, lambda. The summary explains the different cases of vacuum energy density and their effects on the scale factor and the universe's geometry.
📐 Mathematical Analysis of the Friedmann Equations
The paragraph performs a mathematical analysis of the Friedmann equations with different values of the cosmological constant (lambda) and spatial curvature (k). The summary explores the solutions to these equations, leading to various cosmological scenarios, including exponential expansion and bouncing universes.
🔍 Measuring the Cosmological Constant and Dark Energy
This section discusses the efforts to measure the cosmological constant and its implications for our understanding of dark energy. The summary highlights the precision with which the cosmological constant is known and the mystery surrounding its small value.
🤔 The Discrepancy in Vacuum Energy Density
The paragraph addresses the discrepancy between the calculated zero-point energy and the measured expansion rate of the universe. The summary reflects on the fundamental constants of nature and the challenge of understanding why the vacuum energy density is so much smaller than expected.
🌐 Exploring the Implications of a Negative Cosmological Constant
This part explores what happens when the cosmological constant is negative. The summary explains that a negative cosmological constant leads to a universe that expands and then collapses in a big crunch, even in an open, infinite geometry.
🔬 Conclusion and Further Exploration
The final paragraph encourages further exploration of the topic and provides a link to Stanford's website for more information. The summary emphasizes the complexity and ongoing nature of research in cosmology and the importance of continued study.
Mindmap
Keywords
💡Equation of State
💡Scale Factor
💡Cosmological Constant
💡Vacuum Energy
💡Friedmann Equations
💡Hubble Constant
💡Dark Energy
💡Curvature of Space
💡Big Bang
💡Exponential Expansion
💡Sitter Space
Highlights
The importance of understanding the equation of state in cosmology, which describes how the energy density changes with the scale factor.
The concept that the history of the universe can be understood through the time history of the scale factor, a fundamental question in cosmology.
Different models of universe expansion, such as matter dominated and radiation dominated models, and their respective scaling behaviors with time.
The derivation of the relationship between pressure and energy density for different types of universes, including matter and radiation dominated cases.
The role of the speed of light in determining the energy density of non-relativistic particles and its significance in cosmological models.
Explanation of how the energy density scales with the scale factor in both matter and radiation dominated scenarios.
The equation of state for radiation, where pressure is a third of the energy density, and its derivation using a box model filled with photons.
The assumption of isotropy in the velocity distribution of particles in a cosmological context and its implications for the pressure calculation.
The concept of vacuum energy and its equation of state, where the pressure is equal to minus one times the energy density.
The cosmological constant, denoted by lambda, and its relation to vacuum energy, which is a key component of the Friedmann equations.
The behavior of the universe under different values of the cosmological constant (positive, negative, or zero) and their corresponding curvature (k) of space.
The de Sitter space, a solution of Einstein's equations where the universe undergoes exponential expansion due to a positive cosmological constant.
The possibility of a universe with a contracting phase followed by an expansion phase, known as a 'bounce', in the context of a positive cosmological constant and positively curved space.
The implications of a negative cosmological constant on the dynamics of an open (negative k) universe, leading to a big crunch scenario.
The mysterious nature of vacuum energy, its extremely small value, and the discrepancy between calculated zero-point energy and observed cosmological effects.
The impact of vacuum energy on the expansion rate of the universe and the concept of dark energy, highlighting the current understanding and challenges in measuring the equation of state parameter, w.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: