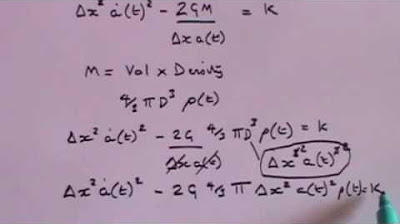Cosmology Lecture 6
TLDRThe video script is an in-depth exploration of cosmological equations and observational facts, focusing on the evolution of our understanding of the universe's structure and expansion. It delves into the Freedman equation, Hubble's constant, and the critical role of the scale factor 'a' in describing the universe's geometry. The lecturer discusses the importance of measuring the Hubble constant, the energy density contributions from radiation, matter, and vacuum energy, as well as the impact of dark matter on these measurements. The script also highlights the historical context of these discoveries, the methods used to determine distances in cosmology, and the significance of the cosmic microwave background. It concludes with observations that have led to the current model of the universe, where dark energy (lambda) dominates, and the universe appears to be spatially flat with a matter density that includes both luminous and dark matter.
Takeaways
- 📐 The basic equation for a homogeneous universe is the Freedman equation, also known as the Hubble function, which describes the expansion rate of the universe.
- ⚖️ The critical density of the universe is determined by the contributions of radiation, matter, vacuum energy (cosmological constant), and curvature.
- 🌌 The scale factor 'a' is essential in the metric of the universe and is related to the energy density and curvature terms in the Friedmann equations.
- 🔍 Astronomers measure the Hubble constant 'H' by observing the relationship between the distance and redshift of celestial objects, which is a fundamental parameter in cosmology.
- 🌟 The energy density in the universe comes from various sources, primarily radiation, ordinary matter (baryonic matter), and vacuum energy (dark energy).
- 🕸️ The concept of dark matter emerged from observations that the mass of galaxies and clusters of galaxies did not behave as expected based on visible matter alone.
- 🌀 Galaxy rotation curves indicated that the mass within a galaxy increases linearly with radius, suggesting a significant amount of unseen, non-luminous matter.
- 🌙 The universe's large-scale structure is believed to have formed first through the gravitational pull of dark matter, which then led to the formation of luminous matter and galaxies.
- ⏳ The age of the universe can be estimated from the Hubble constant, with the current understanding being that the universe is approximately 10 billion years old.
- 🔬 Observations of the Cosmic Microwave Background (CMB) provide further evidence for the role of dark matter and the overall geometry of the universe.
- 📉 The density of dark matter is thought to be higher near the centers of galaxies, which is a key area for searching for potential signals of dark matter interactions or annihilation.
Q & A
What is the basic equation for a homogeneous universe?
-The basic equation for a homogeneous universe is the Freedman equation, which can also be referred to as the Hubble constant squared or the Hubble function. It is represented as (a dot over a) squared.
What are the three main contributions to the energy density in the current universe?
-The three main contributions to the energy density in the current universe are radiation, matter (including both luminous and dark matter), and vacuum energy (or dark energy) associated with the cosmological constant lambda.
How is the curvature term in the Hubble function related to the geometry of the universe?
-The curvature term in the Hubble function has a 'K' in front of it, where 'K' can be either +1, -1, or 0. Positive 'K' corresponds to a spherical geometry, negative 'K' to a hyperbolic geometry, and zero 'K' to a flat geometry.
What is the role of the scale factor 'a' in the metric of the universe?
-The scale factor 'a' is used in the metric to describe the geometry of the universe over time. The metric is given by S squared equals minus DT squared plus the radius at Time Square t squared, and 'a' is involved in determining the spatial part of the metric.
How did Hubble measure the Hubble constant?
-Hubble measured the Hubble constant by observing the relationship between the velocities of galaxies (as determined from redshifts) and their distances. He plotted redshift versus luminosity to establish this relationship.
What are the units of the Hubble constant?
-The Hubble constant is a measure of the inverse time, and its units are typically given in kilometers per second per megaparsec. However, from a theoretical standpoint, the Hubble constant can be considered as simply one over the age of the universe.
What is the significance of the term 'Omega' in cosmology?
-In cosmology, 'Omega' refers to the density parameters, which are the ratios of the various contributions to the energy density of the universe (radiation, matter, vacuum energy, and curvature) to the critical density, divided by the Hubble constant squared. They represent the fraction of the Hubble constant squared today contained in each term.
What is the role of dark matter in the formation of galaxies?
-Dark matter plays a crucial role in the formation of galaxies. It is believed that dark matter first collected into large halos, and then baryonic matter (protons, neutrons, electrons) fell into these dark matter halos, leading to the formation of stars and galaxies.
How does the presence of dark matter affect the rotation curves of galaxies?
-The presence of dark matter affects the rotation curves of galaxies by causing the outer parts of galaxies to have a nearly constant tangential velocity, rather than decreasing with distance from the galactic center as would be expected if only luminous matter were present.
What is the current understanding of the composition of the universe in terms of dark matter, luminous matter, and the cosmological constant?
-The current understanding, based on observations, is that the universe is composed of approximately 30% matter (both luminous and dark matter), 70% vacuum energy or dark energy (lambda), and nearly zero contribution from curvature on large scales.
How can the curvature of the universe be tested or determined?
-The curvature of the universe can be tested by observing the number of galaxies as a function of distance or redshift and the luminosity as a function of redshift. Different curvatures (positive, negative, or zero) would result in different observed relationships between these quantities.
Outlines
🌌 Introduction to Cosmological Equations
The paragraph introduces the Freedman equation, also known as the Hubble constant squared, which is fundamental to understanding the expansion of the universe. It discusses the importance of context in interpreting observational facts and how these facts relate to the equation. The Hubble function, the energy density, and the curvature term are also defined, with the curvature term represented by 'K', which can have values of +1, -1, or 0, corresponding to different spatial geometries. The metric, or the mathematical relationship between space and time, is also mentioned.
🚀 Energy Density Contributions to the Universe
This paragraph delves into the various sources of energy density in the universe, which include radiation, matter, and vacuum energy. It explains how radiation energy density scales with the inverse fourth power of the scale factor 'a', while matter density scales with the inverse cube of 'a'. The cosmological constant 'lambda' represents vacuum energy, which does not dilute with an increase in the scale factor. The curvature term's role in the energy density equation is also discussed.
🌟 Measuring Cosmological Quantities
The focus here is on how astronomers measure the Hubble constant and other cosmological quantities. It discusses the cosmic distance ladder, a method for measuring the distances to celestial objects, and how it relies on standard candles like Cepheid variables and supernovae. The paragraph also covers the measurement of radiation through the Cosmic Microwave Background and the estimation of matter density by observing the luminous matter in galaxies.
📏 The Role of Curvature in Cosmological Models
This paragraph discusses the historical perspective on the role of curvature in the universe's geometry. It talks about how the ratios of radiation, matter, and the cosmological constant, represented as Omega values, have changed over time. The importance of these ratios adding up to 1 is emphasized, which is a result of their definitions in terms of the Hubble constant squared. The paragraph also touches on the misconceptions about the universe's curvature and size based on older cosmological models.
🕰️ Time Variation of the Hubble Constant
The paragraph explains how the Hubble constant varies with time in a matter-dominated universe. It describes the relationship between the Hubble constant and the age of the universe, stating that the Hubble constant is essentially one over the age of the universe. The historical context of Hubble's measurements and the implications of these measurements on the perceived age of the universe are also discussed.
🌑 Dark Matter and its Effects on Cosmology
This paragraph introduces the concept of dark matter and its significance in cosmology. It explains how dark matter does not radiate or interact strongly with electromagnetic forces, making it difficult to detect. The paragraph also discusses the historical discovery of dark matter through the anomalous behavior of galaxies and galaxy clusters, which could not be explained by the presence of luminous matter alone.
🌀 Galaxy Rotation Curves and Dark Matter Distribution
The discussion here centers on the rotation curves of galaxies and how they provide evidence for dark matter. It explains that the observed flat rotation curves, indicating a constant velocity of stars at different radii from the galactic center, suggest a distribution of mass that increases linearly with the radius. This is in contrast to the expectation from luminous matter alone, which would predict a decrease in velocity with distance from the center.
🌌 Dark Matter Halos and Galaxy Formation
This paragraph explores the idea that dark matter forms halos around galaxies and that these halos influence the formation of galaxies. It discusses the hypothesis that dark matter collected first into these halos, which then attracted baryonic matter, leading to the formation of stars and galaxies. The paragraph also touches on the controversy surrounding the nature of dark matter and the possibility of it being made up of particles that are weakly interacting or not electrically charged.
🔍 Detecting Dark Matter and its Aggregated State
The focus of this paragraph is on the methods for detecting dark matter and understanding its aggregated state. It discusses the possibility of dark matter being made up of particles that are so weakly interacting that they may not form dust or gas but exist as individual particles. The paragraph also explores the idea that dark matter could be detected through its gravitational effects or potentially through future particle collisions.
📉 Testing Cosmological Models Through Observation
This paragraph outlines how cosmological models can be tested through observations of the universe. It discusses the importance of measuring the number of galaxies as a function of distance or redshift and how this can provide insights into the curvature of space. The paragraph also explains how luminosity as a function of redshift can be used to test cosmological models and determine the nature of the universe's expansion.
🧮 The Friedmann Equations and Model Fitting
The paragraph details the use of the Friedmann equations to calculate observable quantities such as the number of galaxies per unit redshift and the relationship between redshift and luminosity. It emphasizes the process of creating a model with specific parameters, calculating the observable signatures, and comparing these with actual observations to find the best fit. The importance of the cosmological constant and its role in the current model of the universe is highlighted.
🔄 The Evolution of Omega Values in the Universe
This paragraph discusses the evolution of the Omega values, which represent the ratios of different components' densities in the universe. It explains how these values change over time, with radiation dominating in the past, matter being significant in the recent past, and the cosmological constant (lambda) expected to dominate in the future. The paragraph also touches on the implications of these changes for the universe's geometry and ultimate fate.
🔬 Precision Cosmology and Systematic Deviations
The final paragraph emphasizes the precision achieved in cosmology, noting that the current model fits observational data to within about one percent. It mentions ongoing efforts to measure cosmic parameters with even greater accuracy, such as through the study of the cosmic microwave background. The paragraph also acknowledges the possibility of systematic deviations that could indicate new physics or a refinement of the current model.
Mindmap
Keywords
💡Hubble Constant
💡Scale Factor (a)
💡Cosmological Constant (Lambda)
💡Dark Matter
💡Curvature (K)
💡Redshift
💡Friedmann Equation
💡Cosmic Microwave Background (CMB)
💡Luminous Matter
💡Omega (Ω) Parameters
💡Standard Candles
Highlights
The Freedman equation, also known as the Hubble function, is fundamental to understanding the expansion of the universe.
The Hubble constant is not truly constant; it varies over time and is related to the age of the universe.
The energy density of the universe has three main contributions: radiation, matter, and vacuum energy.
The curvature term in the cosmological equations is represented by K and determines the geometry of the universe.
The scale factor 'a' is crucial for understanding the metric and the expansion of the universe over time.
Observational quantities such as the Hubble constant, radiation density, and matter density can be measured and related to cosmological models.
The Cosmic Microwave Background provides evidence for the radiation energy density in the universe.
Matter in the universe, both luminous and dark, contributes to the energy density and is crucial for understanding galaxy formation.
The concept of dark matter was introduced to explain the discrepancies in galaxy rotation curves and the mass of galaxy clusters.
Dark matter is believed to be non-luminous and does not interact strongly with electromagnetic forces.
The density of dark matter is higher near the centers of galaxies, suggesting a spherical distribution rather than a spiral arm configuration.
The Lambda-CDM model, which includes a cosmological constant, is used to explain the observed luminosity and galaxy distribution.
The Hubble constant can be measured by observing the relationship between redshift and distance or luminosity.
The age of the universe can be estimated using the Hubble constant and is consistent with a matter-dominated universe.
Observations of supernovae and the cosmic microwave background are used to determine the parameters of the universe's expansion.
The universe's geometry, determined by K, affects the observed number of galaxies and their luminosity as a function of redshift.
Current cosmological observations suggest a flat universe with a significant contribution from dark energy (Lambda).
The isotropic and homogeneous distribution of galaxies is a key assumption in modern cosmology, supported by observations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: