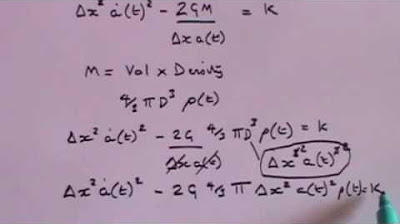Cosmology Lecture 2
TLDRThe video script is a detailed lecture on the dynamics of an expanding universe, touching upon the fundamental equations of an expanding universe as derived from Newton's laws and generalizing to include the effects of different forms of energy, such as radiation and dark energy. The lecturer explains the concept of the scale factor 'a' and its relation to the Hubble constant, and how it describes the expansion of the universe over time. The transition from radiation-dominated to matter-dominated expansion is discussed, highlighting the different expansion rates characterized by t^(1/2) and t^(2/3), respectively. The script also explores the implications of the universe's energy content, including the potential for negative energy and its impact on the geometry of space. The lecturer further delves into the behavior of photons in an expanding universe, describing how the energy of photons decreases with the expansion, a phenomenon rooted in the adiabatic invariant principle. The lecture concludes with a teaser for future discussions on dark energy and its role in the accelerated expansion of the universe.
Takeaways
- 📚 The universe's expansion can be described by Newton's equations for most practical purposes, especially on a local scale where galaxies are moving at non-relativistic speeds.
- 🌌 Einstein's equations, which involve curved space-time, become more relevant when considering the universe's large-scale structure and the potential curvature of space itself.
- 📐 At very large distances, the universe appears to be flat, which allows for the use of Newtonian physics to study the motion of galaxies, despite the universe's overall possible curvature.
- 💡 Photons, which move at the speed of light, require a modification to the equations because their rapid movement means they contribute significantly to the energy density of the universe.
- ✨ Neutrinos and cosmic microwave background radiation are examples of fast-moving particles and radiation that must be considered in the cosmic equations, especially in the early universe when radiation dominated.
- 🌟 The scale factor 'a' is used to describe the universe's expansion, with its rate of change being important for understanding the universe's dynamics.
- ⏱️ Time as a function of the scale factor can be used to derive the expansion history of the universe, with different behaviors based on the total energy of the system.
- 🔢 The Friedmann equations, derived from general relativity, provide a more comprehensive model for the universe's expansion, including the effects of different types of energy densities.
- ⚙️ The energy density of radiation decreases more rapidly than that of matter as the universe expands, leading to a transition from a radiation-dominated to a matter-dominated universe over time.
- 🌞 The behavior of the universe in the past was heavily influenced by radiation, while the present and future are more influenced by matter and, potentially, dark energy.
- 🔑 The geometry of the universe (flat, positively curved, or negatively curved) plays a crucial role in its expansion history and is connected to the constant 'k' in the Friedmann equations.
Q & A
What is the significance of Newton's equations in understanding the expanding universe?
-Newton's equations are significant for the most part in understanding the expanding universe, especially on a local scale where galaxies are moving with non-relativistic velocities. They provide a basis for studying the motion and mutual interaction of galaxies without needing to account for relativistic effects.
How does the concept of a curved space-time relate to the universe's expansion?
-Einstein's equations, which deal with curved space-time, become relevant when considering the universe's expansion on a larger scale. While the universe may appear flat on small scales, it could be curved on larger scales, which would affect the overall understanding of its expansion.
What is the role of the scale factor 'a' in cosmological equations?
-The scale factor 'a' represents the ratio of the current size of the universe to its size at a specific reference time. It is crucial in cosmological equations as it accounts for the expansion or contraction of the universe over time. Ratios of 'a' at different times are particularly meaningful as they record the history of the universe's expansion.
Why is the Hubble constant (a dot over a) an important quantity in cosmology?
-The Hubble constant is important because it quantifies the rate of expansion of the universe. It is derived from the time derivative of the scale factor 'a' and provides insight into the dynamics of the cosmic expansion.
How does the energy density of the universe change with the scale factor 'a'?
-The energy density of the universe, denoted by rho (ρ), is related to the mass within a grid cell (nu) and the scale factor 'a'. As the universe expands, the energy density decreases because the same mass is distributed over an increasing volume. Specifically, rho is proportional to nu divided by a cubed.
What is the Friedman equation and how does it relate to the expansion of the universe?
-The Friedman equation is a set of equations derived from Einstein's field equations of general relativity that describe the expansion of the universe. It relates the scale factor 'a', its time derivative (representing the expansion rate), the energy density, and the curvature of space to the dynamics of the universe's expansion.
What is the difference between the behavior of the universe with positive, negative, and zero total energy?
-A universe with positive total energy will continue to expand indefinitely, while a universe with negative total energy will eventually stop expanding and contract, leading to a collapse. A universe with zero total energy is at the 'edge' of these two scenarios, where the expansion velocity is at the escape velocity, and it neither accelerates nor decelerates significantly.
How does the presence of radiation in the universe affect its expansion?
-The presence of radiation affects the expansion of the universe by contributing to the energy density. As the universe expands, the energy density of radiation decreases more rapidly than that of matter, since it scales with the inverse fourth power of the scale factor 'a'. This leads to a different expansion rate, which can be derived by considering the energy density of radiation in the Friedman equation.
What is the adiabatic invariant in the context of an expanding universe?
-The adiabatic invariant is a property of a system that remains constant during a slow, adiabatic change. In the context of an expanding universe, it refers to the number of nodes or the number of times a wave (like a photon) passes through zero. As the universe expands, the wavelength of a photon increases to maintain this invariant, which results in a decrease in the photon's energy.
How does the energy of a photon change as the universe expands?
-As the universe expands, the energy of a photon decreases. This is because the wavelength of the photon stretches in proportion to the expansion of the universe, leading to a decrease in the photon's energy. This phenomenon is consistent with the adiabatic invariant principle, where the number of nodes (or zeros) of the photon wave remains constant.
What is the role of dark energy in the expansion of the universe?
-Dark energy is a form of energy that permeates all of space and tends to accelerate the expansion of the universe. It is a relatively recent discovery and is thought to be responsible for the observed accelerated expansion rate of the universe, which cannot be explained by the energy contributions from matter and radiation alone.
Outlines
📚 Generalizing the Universe's Expansion
The paragraph discusses the validity of Newton's equations in describing an expanding universe and introduces the concept of curved space-time as described by Einstein's equations. It explores the idea that while the universe appears flat on a small scale, it may be curved on a larger scale, potentially taking the shape of a sphere. The lecturer also touches on the behavior of galaxies moving apart and the potential need to modify equations if particles are found to move at a significant fraction of the speed of light.
🌌 Homogeneous Space and the Grid Model
This section delves into the assumptions of a homogeneous universe filled with galaxies, using a grid model to represent space. It explains the concept of density (rho) and how it is measured in kilograms per cubic meter. The importance of the grid spacing (a) and its ratios rather than its absolute value are discussed, highlighting the Hubble constant's significance as a ratio of these spacings over time.
🔍 Deriving the Universe's Expansion Equations
The paragraph reviews the derivation of the equations governing the universe's expansion. It discusses the assumptions made, such as the universe being filled with galaxies and the use of Newton's theorem to simplify the calculations. The lecturer explains how the conservation of energy principle led to the derivation of the equation relating the scale factor's rate of change to the density of matter and a constant involving the gravitational constant and the mass within a sphere.
🌟 Expansion with Zero Total Energy
The discussion focuses on the scenario where the universe's total energy is zero, which corresponds to galaxies moving at the escape velocity. The lecturer derives the Friedman equation by considering the kinetic and potential energy of a galaxy and relates the density of matter to the mass within a grid cell. The numerical value of the constant in the equation is shown to be arbitrary due to grid definition flexibility.
🔧 Solving the Scale Factor Differential Equation
The paragraph demonstrates the solution to the differential equation for the scale factor of the universe. It starts with the equation derived from energy conservation and manipulates it to express time as a function of the scale factor. The solution reveals that the scale factor is proportional to the two-thirds power of time, indicating a decelerating universe that never comes to rest.
🌱 Early Universe Dominated by Radiation
The focus shifts to the early universe, where radiation, not mass, was the most dominant form of energy. The lecturer discusses the importance of understanding the behavior of a universe filled with photons and how the energy density of radiation changes with the expansion of the universe. It contrasts radiation with matter and introduces the concept that the energy density of radiation decreases with the square of the scale factor.
🌌 The Friedman Equation and Cosmic Expansion
This section derives the Friedman equation for non-zero energy, which accounts for the total energy of the universe and its impact on cosmic expansion. The lecturer explains how the sign of the total energy (positive, negative, or zero) influences the fate of the universe, with positive energy leading to endless expansion, negative energy to a collapse, and zero energy to a critical point with implications yet to be explored.
🔬 The Interplay of Geometry and Energy in the Universe
The paragraph connects the Friedman equation with general relativity, highlighting the role of geometry on the left side and energy-momentum on the right. It discusses the transition from Newtonian to relativistic mechanics and the importance of considering all forms of energy density, including rest mass energy and radiation energy, in the context of an expanding universe.
🌉 Cosmic Expansion and Energy Conservation
The discussion addresses the concept of energy conservation in an expanding universe. It explores how the energy associated with the expansion rate appears as a negative term in the energy conservation equation, implying that as the universe expands, the energy in the form of matter and radiation decreases. The lecturer also touches on the subtleties of energy conservation in the context of general relativity.
🌐 Geometries of the Universe and Cosmic Fate
The paragraph examines the implications of different geometries (flat, positively curved, and negatively curved) on the fate of the universe. It relates the curvature of space to the term involving the scale factor in the Friedman equation and suggests that the universe's geometry and the sign of the total energy determine whether the universe will expand indefinitely, collapse, or reach a stable size.
🌞 The Universe's Expansion and the Speed of Light
The lecturer addresses questions about the apparent speed of objects in an expanding universe and how it relates to the speed of light. It clarifies that while objects can recede from each other faster than the speed of light due to the expansion of space, this does not violate the principle that information cannot travel faster than light. The concept of an event horizon is introduced, where objects may eventually disappear from view due to the accelerated expansion of the universe.
🎓 Adiabatic Expansion and Photon Energy
The final paragraph discusses the adiabatic invariant principle in the context of an expanding universe. It explains that as the universe expands, the wavelength of a photon increases, and its energy decreases. This is analogous to the behavior of a violin string or a gas in a box, where the energy of the system decreases if the expansion is done slowly (adiabatically), leading to a cooling effect.
Mindmap
Keywords
💡Newton's equations
💡Einstein's equations
💡Expanding Universe
💡Scale Factor (a)
💡Hubble Constant
💡Curvature of Space
💡Friedman Equations
💡Energy Density
💡Cosmic Microwave Background (CMB)
💡Dark Energy
💡Adiabatic Invariant
Highlights
The equations of an expanding universe were discussed, highlighting Newton's equations' adequacy for most cases.
Einstein's equations, which deal with curved space-time, were contrasted with Newton's equations for understanding the universe's structure.
The possibility of space being curved was explored, with the current appearance of flatness but potential for a curved average on a larger scale.
The concept of 'very neighboring galaxies' was introduced to describe galaxies close enough to appear flat despite the universe's possible curvature.
Newton's equations were deemed suitable for studying the local behavior of galaxies moving apart, under the assumption of non-relativistic velocities.
The special case where galaxies move past each other at a significant fraction of the speed of light was discussed, noting the need for equation modification in such instances.
Neutrinos and photons were identified as particles that move close to the speed of light, affecting the need to modify equations to account for relativistic effects.
The assumption of a homogeneous and isotropic universe filled with galaxies was reviewed, leading to the introduction of the density parameter rho.
The concept of a grid laid on the universe was used to define the scale factor 'a' and its relation to the physical distance between galaxies.
The Hubble constant was derived from the time derivative of the scale factor 'a', providing insight into the expansion rate of the universe.
The mass within a single cubic cell of the grid, denoted by 'nu', was discussed in relation to the density 'rho' and how it changes with the grid size.
The Friedman equation was derived from the conservation of energy, relating the scale factor, mass density, and a constant related to the total energy.
Three different behaviors of the universe were predicted based on the sign of the total energy: positive (expanding forever), negative (eventually collapses), and zero (escape velocity).
The transition from a radiation-dominated to a matter-dominated universe was explained, showing how the expansion rate changes over time.
The impact of dark energy on the universe's accelerated expansion was alluded to, promising a deeper exploration in subsequent discussions.
The concept of an adiabatic expansion was introduced, explaining why the energy of a photon decreases as the universe expands.
The conservation of energy in an expanding universe was discussed, addressing the subtleties of energy transfer between different components.
The geometry of space was connected to the constant 'c' in the Friedman equation, foreshadowing a discussion on the spatial curvature of the universe.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: