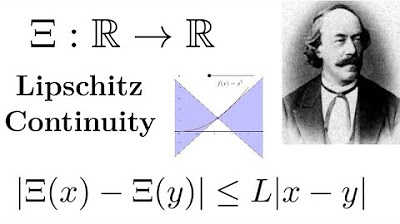Lipschitz functions
TLDRThis video script delves into the concept of Lipschitz functions, which are mathematical functions that have a bounded rate of change. The presenter explains that a function is considered Lipschitz if there exists a real number K such that the absolute difference in outputs (f(X) - f(Y)) is always less than or equal to K times the absolute difference in inputs (|X - Y|) for any two points X and Y within the function's domain. The script illustrates the idea with examples, contrasting a Lipschitz function with a non-Lipschitz function by examining the slopes of lines connecting points on their graphs. It further discusses the relationship between Lipschitz functions and uniform continuity, proving that if a function is Lipschitz, it is also uniformly continuous. However, the converse is not always true, as demonstrated by the example of the square root function on the domain [0, 2], which is uniformly continuous but not Lipschitz. The summary concludes by emphasizing the stronger property of Lipschitz functions compared to uniformly continuous ones.
Takeaways
- 📐 **Lipschitz Functions Defined**: A function is Lipschitz if there exists a positive real number K such that for any two points X and Y in the domain, the absolute difference in the function's outputs is less than or equal to K times the absolute difference in the inputs.
- 🔍 **Bounding the Slope**: For a function to be Lipschitz, the slope of the line between any two points on the graph of the function must be bounded above by K.
- 📈 **Lipschitz vs. Non-Lipschitz**: A function with a graph that has lines between points with consistently bounded slopes (by K) is Lipschitz, whereas if the slopes become arbitrarily steep as points get closer, it is not.
- 🧵 **Uniform Continuity from Lipschitz**: If a function is Lipschitz, it is also uniformly continuous. This is because a uniform bound on the rate of change (the Lipschitz constant) implies uniform continuity.
- 🔗 **Proof Sketch**: To show a Lipschitz function is uniformly continuous, one can choose a delta value (Δ) as epsilon over K, where epsilon is any positive number and K is the Lipschitz constant.
- ➿ **Hierarchy of Functions**: There is a hierarchy among functions: all Lipschitz functions are uniformly continuous, but not all uniformly continuous functions are Lipschitz.
- 🚫 **Non-Lipschitz Example**: The function f(x) = √x on the domain [0, 2] is uniformly continuous (due to being defined on a closed bounded interval) but not Lipschitz, as for any K, there exists an X such that the slope between X and 0 exceeds K.
- 🔢 **Domain Restriction**: The property of being Lipschitz or uniformly continuous can be dependent on the domain of the function; a function may be Lipschitz on one domain and not on another.
- 🔄 **Slope Comparison**: A key method to determine if a function is Lipschitz is to compare the slope of the secant lines between points on the graph to the constant K.
- 📉 **Unbounded Growth**: A function whose secant lines' slopes increase without bound as points approach each other is not Lipschitz, indicating the lack of a global upper bound on the rate of change.
- 🤔 **Understanding Lipschitz**: Grasping the concept of Lipschitz functions involves understanding the relationship between the rate of change of a function and the constant K that bounds this rate across the domain.
Q & A
What is a Lipschitz function?
-A Lipschitz function is a function whose rate of change has a bounded slope. Specifically, for a function to be Lipschitz on a domain, there must exist a positive real number K such that the absolute difference in the function's outputs (f(X) - f(Y)) is always less than or equal to K times the absolute difference in the inputs (|X - Y|) for every pair of points X and Y within the domain.
What is the relationship between the Lipschitz condition and the slope of the line connecting two points on the graph of the function?
-The Lipschitz condition implies that the slope of the line connecting any two points on the graph of the function is always bounded above by the constant K. This means that no matter which two points you choose from the domain, the slope of the line segment connecting these points on the graph will never exceed K.
Why is the Lipschitz condition important in the context of uniform continuity?
-The Lipschitz condition is important because if a function is Lipschitz on a domain, it is also uniformly continuous on that domain. This is significant because uniform continuity guarantees that for any given positive number (epsilon), there exists a positive number (delta) such that for any two points in the domain that are less than delta apart, their function values are less than epsilon apart.
How does one prove that a Lipschitz function is uniformly continuous?
-To prove that a Lipschitz function is uniformly continuous, one starts by assuming that the function is Lipschitz with a constant K. Given epsilon greater than zero, choose delta to be epsilon over K. Then, for any two points X and Y in the domain that are less than delta apart, the absolute difference in their function values is less than K times the absolute difference in their inputs, which is less than K times delta, and hence less than epsilon, proving uniform continuity.
What is the hierarchy of functions in terms of continuity, uniform continuity, and Lipschitz functions?
-The hierarchy of functions from least to most restrictive is as follows: all functions, continuous functions, uniformly continuous functions, and Lipschitz functions. Every Lipschitz function is uniformly continuous, and every uniformly continuous function on a closed and bounded interval is continuous. However, the reverse implications do not hold; there are functions that are continuous but not uniformly continuous, and functions that are uniformly continuous but not Lipschitz.
Can you provide an example of a function that is uniformly continuous but not Lipschitz?
-Yes, the function f(x) = sqrt(x) on the domain [0, 2] is an example of a function that is uniformly continuous but not Lipschitz. While it is uniformly continuous because it is continuous on a closed bounded interval, it is not Lipschitz since for any positive number K, one can find an X in the interval (0, 1/K^2) such that the slope of the line connecting (X, f(X)) and (0, f(0)) exceeds K.
How does the example of the function f(x) = sqrt(x) on [0, 2] demonstrate that a uniformly continuous function is not necessarily Lipschitz?
-The function f(x) = sqrt(x) demonstrates this by showing that for any positive constant K, it is possible to find two points X and Y (with Y chosen as 0 for simplicity) such that the slope of the line connecting these points on the graph of f(x) is greater than K. This unbounded slope indicates that there is no single constant K that can bound the rate of change for all points in the domain, hence f(x) is not Lipschitz.
What does it mean if a function is not Lipschitz on a certain domain?
-If a function is not Lipschitz on a certain domain, it means that there is no single real number K that can bound the absolute difference in the function's outputs by K times the absolute difference in the inputs for all points within that domain. In other words, the function's rate of change (or slope) can become arbitrarily steep as you compare points closer together within the domain.
How does the concept of Lipschitz functions relate to real-world applications?
-Lipschitz functions have applications in various fields such as optimization, control theory, and machine learning. They are useful because they provide a bound on the rate of change, which can be important for ensuring stability in systems, convergence in algorithms, and robustness in models.
What is the significance of the constant K in the context of a Lipschitz function?
-The constant K in the context of a Lipschitz function is the Lipschitz constant. It is the maximum rate at which the function's output can change with respect to changes in its input. A smaller Lipschitz constant indicates a more stable function with a more predictable rate of change.
Can a function be Lipschitz without being differentiable everywhere on its domain?
-Yes, a function can be Lipschitz without being differentiable everywhere on its domain. The Lipschitz condition only requires the existence of a bound on the rate of change (the slope of the function), not necessarily the existence of a derivative at every point. There are functions that are Lipschitz but have points of non-differentiability.
What is the difference between a Lipschitz function and a function with a bounded derivative?
-A function with a bounded derivative has a bounded rate of change at every point in its domain, meaning the derivative (slope) is always within a certain range. A Lipschitz function, on the other hand, does not require the derivative to be bounded at every point, but rather that there exists a constant K that bounds the ratio of the change in output to the change in input for any two points in the domain.
Outlines
📐 Introduction to Lipschitz Functions
This paragraph introduces the concept of Lipschitz functions, which are real-valued functions on a subset of the real line with a property that the absolute difference in their outputs is bounded by a constant K times the absolute difference in their inputs for any two points in the domain. The paragraph explains that if such a constant K exists, the function is Lipschitz. It also illustrates the idea by rearranging the inequality to resemble a slope, indicating that the slope of the line between any two points on the graph of a Lipschitz function is always less than or equal to K. The yellow graph in the example is a Lipschitz function, while the other graph is not, as it does not have a bounded slope between any two points.
🔗 Lipschitz Functions and Uniform Continuity
The second paragraph discusses the relationship between Lipschitz functions and uniform continuity. It states that if a function is Lipschitz on a domain, it is also uniformly continuous on that domain. The proof is outlined by showing that for any given epsilon greater than zero, a delta can be found that depends only on epsilon, such that for any two points within delta of each other, the outputs are within epsilon of each other. This is achieved by using the Lipschitz constant K to relate the difference in outputs to the difference in inputs, and then choosing delta to be epsilon over K. The paragraph also presents a hierarchy of functions, where all Lipschitz functions are uniformly continuous, but not all uniformly continuous functions are Lipschitz.
🚫 Counterexample: Uniform Continuity Without Lipschitz
The final paragraph provides a counterexample to show that uniform continuity does not imply Lipschitz continuity. It uses the function f(x) = √x on the domain [0, 2], which is uniformly continuous due to the continuity of the function on a closed bounded interval. However, it is shown that this function is not Lipschitz by demonstrating that for any positive number K, there exists an x in the interval (0, 1/K^2) such that the slope of the line between x and 0 on the graph of the function is greater than K. This indicates that the slope between points on the graph is not bounded, and thus the function does not satisfy the Lipschitz condition.
Mindmap
Keywords
💡Lipschitz function
💡Domain
💡Uniform continuity
💡Slope
💡Real line
💡Bounding above
💡Continuous function
💡Closed bounded interval
💡Epsilon and Delta
💡Hierarchical relationship
💡Square root function
Highlights
A function is considered Lipschitz if there exists a positive real number K such that the absolute difference in outputs is always less than or equal to K times the absolute difference in inputs for any two points in the domain.
The concept of Lipschitz functions is easier to understand by considering the slope of the line between any two points on the graph of the function, which should never exceed K.
Lipschitz functions have the property that their rate of change (slope) is bounded, which is a strong condition that not all functions can satisfy.
If a function is Lipschitz, it is also uniformly continuous on its domain, which is a significant property in the analysis of functions.
The proof of Lipschitz functions being uniformly continuous involves showing that for any given epsilon, there exists a delta that works for all pairs of points in the domain.
The relationship between the difference in outputs and inputs is used to establish the uniform continuity of Lipschitz functions.
There is a hierarchy of functions, with Lipschitz functions being a subset of uniformly continuous functions, which in turn are a subset of all continuous functions.
Not all uniformly continuous functions are Lipschitz, indicating that being Lipschitz is a stronger condition.
An example is provided to illustrate a function that is uniformly continuous but not Lipschitz, specifically the square root function on the domain from 0 to 2.
The square root function on the interval [0, 2] is shown to not be Lipschitz by demonstrating that for any positive K, a suitable X can be found where the slope between X and a point exceeds K.
The slope of the line connecting any two points on the graph of a Lipschitz function must be bounded above by K, which is not the case for the square root function as X approaches 0.
The concept of Lipschitz continuity is important in various fields of mathematics, including analysis and optimization.
Understanding the difference between Lipschitz and uniformly continuous functions is crucial for the study of real analysis and the behavior of functions on different domains.
The video provides a clear visual representation of Lipschitz functions using graphs, aiding in the comprehension of abstract mathematical concepts.
The transcript emphasizes the importance of the constant K in defining the Lipschitz property and its role in bounding the rate of change of a function.
The mathematical proof provided in the transcript demonstrates the logical process of proving that Lipschitz functions are uniformly continuous.
The transcript concludes with a reminder of the relationship between different types of functions, reinforcing the concept that Lipschitz functions are a special case within the broader category of continuous functions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: