What is a Lipschitz condition?
TLDRIn this presentation, Chris Tisdale, a mathematician from the University of New South Wales, delves into the concept of the Lipschitz condition in the context of ordinary differential equations (ODEs) and initial value problems. He explains that Lipschitz conditions are vital for understanding the qualitative properties of equations and are linked to contractive maps, which help establish the uniqueness of solutions and their approximation methods. Tisdale provides a fundamental inequality that defines the Lipschitz condition and discusses its importance in the theory of ODEs. He also presents a lemma that offers sufficient conditions to verify the Lipschitz condition, which involves checking the continuity and boundedness of the partial derivative of the function under consideration. Through several examples, he illustrates how to apply the lemma and the direct definition of the Lipschitz condition to determine if a function satisfies it within a given set. The presentation concludes with the classic Picard-Lindelöf theorem, which guarantees the local existence and uniqueness of solutions to initial value problems under Lipschitz conditions, and a corollary that simplifies the application of the theorem by focusing on the existence and continuity of the partial derivative within a rectangle. Tisdale's presentation is accessible to anyone with a basic understanding of calculus and provides a clear insight into the significance of Lipschitz conditions in mathematical analysis.
Takeaways
- 📚 Chris Tisdale, a mathematician at the University of New South Wales, discusses the concept of the Lipschitz condition in the context of ordinary differential equations (ODEs) and initial value problems.
- 🔍 The Lipschitz condition is fundamental for studying the qualitative properties of equations and is connected with contractive maps, which can be used to show the uniqueness of solutions and how to approximate them.
- 📉 A function F satisfies the Lipschitz condition on a set D if there exists a non-negative constant L such that the inequality |F(x1, y1) - F(x2, y2)| ≤ L * |(x1, y1) - (x2, y2)| holds for all points in D.
- 🧩 The analysis of whether a Lipschitz condition holds depends on the structure of the function F and the set D, and it can sometimes be easily verified.
- 📏 A lemma is presented that provides sufficient conditions for F to satisfy the Lipschitz condition if the partial derivative of F with respect to its second variable exists, is continuous on D, and is bounded by a constant K.
- 📐 The proof of the lemma is based on the fundamental theorem of calculus, which allows for the transformation of the difference between function values into an integral involving the derivative.
- 🤔 The examples provided illustrate how to apply the lemma to determine if a function satisfies the Lipschitz condition on a given set, with one example showing satisfaction on a rectangle and another not on an infinite strip.
- 📈 The importance of the Lipschitz condition is highlighted by the Picard-Lindelöf theorem, which states that if F satisfies the Lipschitz condition on a rectangle, then the initial value problem has a unique solution in some interval containing the initial point.
- 📝 A corollary to the Picard-Lindelöf theorem is presented, which states that if the partial derivative of F exists and is continuous on a rectangle R and is bounded, then F satisfies the Lipschitz condition on R, ensuring a unique local solution.
- 📊 The concept of convex sets is introduced as a generalization of rectangles and infinite strips, where a set is convex if the line segment between any two points in the set lies entirely within the set.
- 🔗 The presentation concludes with references to further reading on the topic, emphasizing the importance of the Lipschitz condition in the study of ODEs.
Q & A
What is the main topic of Chris Tisdale's presentation?
-The main topic of the presentation is the concept of a Lipschitz condition within the context of ordinary differential equations and initial value problems.
What is a Lipschitz condition?
-A Lipschitz condition is a fundamental inequality that a function of two variables must satisfy on a set D, if there exists a non-negative constant L such that the inequality holds for all pairs of points in D.
Why are Lipschitz conditions important in the study of ordinary differential equations?
-Lipschitz conditions are important because they are connected with contractive maps and can be used to show when solutions to differential equations have a unique solution and to approximate the solutions once their existence and uniqueness are known.
What is the basic form of the inequality that defines a Lipschitz condition?
-The basic form of the inequality is that for a function F and a constant L, for all pairs of points (x, y) and (x', y') in the set D, the absolute value of the difference F(x, y) - F(x', y') is less than or equal to L times the absolute value of the difference (x - x', y - y').
What is the significance of the lemma presented by Chris Tisdale?
-The lemma provides sufficient conditions that guarantee a Lipschitz condition will be satisfied, which is useful for determining when a function F satisfies the Lipschitz condition without having to directly verify the inequality for all pairs of points in the set D.
What are the conditions under which the lemma guarantees a Lipschitz condition is satisfied?
-The conditions are that the function F is defined on a set D, which is either a rectangle or an infinite strip, the partial derivative of F with respect to its second variable exists and is continuous on D, and there is a non-negative constant K such that the derivative is bounded by K on the set D.
Why is the partial derivative of F with respect to its second variable important in the lemma?
-The partial derivative of F with respect to its second variable is important because it needs to be continuous on the set D and bounded by a constant K for the lemma to guarantee that F satisfies the Lipschitz condition.
What is the fundamental theorem of calculus used for in the proof of the lemma?
-The fundamental theorem of calculus is used to express the difference between the function values at two points as the integral of the derivative, which allows for the establishment of the inequality that characterizes the Lipschitz condition.
What is the Picard-Lindelöf theorem, and how is it related to Lipschitz conditions?
-The Picard-Lindelöf theorem is a classic result in the theory of ordinary differential equations that states if a function F satisfies a Lipschitz condition on a rectangle, then the initial value problem has a unique solution on some interval containing the initial point. It is related to Lipschitz conditions because these conditions are a key requirement for the theorem to apply.
What does it mean for a set to be convex?
-A set is convex if for any two points within the set, the entire line segment that connects them lies entirely within the set.
How can the concept of convex sets be applied in the context of Lipschitz conditions?
-Convex sets can be used to extend the application of lemma one to more general sets beyond rectangles or infinite strips. If a function satisfies the Lipschitz condition on a convex set, it can provide a simpler way to ensure the existence and uniqueness of solutions to initial value problems.
Outlines
📘 Introduction to Lipschitz Conditions in ODEs
Chris Tisdale, a mathematician from the University of New South Wales, introduces the concept of Lipschitz conditions within the context of ordinary differential equations (ODEs), particularly focusing on initial value problems. He explains that Lipschitz conditions are crucial for studying the qualitative properties of equations and are linked to contractive maps. These conditions help in establishing the uniqueness of solutions and methods for approximating them. The general first-order initial value problem for ODEs is discussed, emphasizing the importance of Lipschitz conditions for understanding the existence, uniqueness, and approximation of solutions.
📔 Verifying Lipschitz Conditions and Sufficient Conditions
The presentation delves into how to verify if a function F satisfies the Lipschitz condition on a set D. A function meets the criteria if there exists a non-negative constant L that ensures a specific inequality holds for all points in D. A lemma is introduced, providing sufficient conditions under which the Lipschitz condition is guaranteed. These conditions relate to the continuity and boundedness of the partial derivative of F with respect to its second variable on the set D. The proof of the lemma is outlined using the fundamental theorem of calculus, and examples are provided to illustrate the application of the lemma in verifying the Lipschitz condition for different functions and sets.
📒 Examples of Applying Lemma 1 to Verify Lipschitz Conditions
Chris presents two examples to demonstrate the application of Lemma 1. In the first example, the function F is 'cosine T plus y cubed', and the set D is a rectangle. By calculating the partial derivative and showing it is bounded within the rectangle, it is confirmed that F satisfies the Lipschitz condition with a Lipschitz constant K equal to 3. The second example modifies the set D to an infinite strip. Here, the partial derivative is continuous and well-defined, but there is no bounding constant K for the derivative on the unbounded strip. Thus, Lemma 1 cannot be applied, and it is concluded that F does not satisfy the Lipschitz condition on this set. A third example with the function F as 't plus Tan inverse y' is also discussed, showing that this function does satisfy the Lipschitz condition everywhere due to the bounded nature of its derivative.
📕 Lipschitz Conditions in the Context of Initial Value Problems
The video concludes with the application of Lipschitz conditions to initial value problems in ODEs. The Picard-Lindelöf theorem is highlighted, which states that if a function F is continuous, maps a rectangle into real numbers, and satisfies a Lipschitz condition on that rectangle, then the initial value problem has a unique solution on an interval containing a given point. A corollary to the theorem is also presented, which removes the explicit Lipschitz condition and instead uses the conditions derived from Lemma 1, such as the existence and continuity of the partial derivative and its boundedness, to ensure the same conclusion of a unique local solution. The presentation wraps up with references to further reading on the subject.
Mindmap
Keywords
💡Lipschitz condition
💡Ordinary Differential Equations (ODEs)
💡Initial Value Problem
💡Contractive Maps
💡
💡Partial Derivative
💡Fundamental Theorem of Calculus
💡Picard-Lindelöf Theorem
💡Convex Set
💡Unique Solution
💡Approximation of Solutions
Highlights
Chris Tisdale, a mathematician at the University of New South Wales, discusses the concept of a Lipschitz condition in the context of ordinary differential equations and initial value problems.
Lipschitz conditions are crucial for studying the qualitative properties of equations and are linked with contractive maps, aiding in demonstrating the uniqueness of solutions and their approximation.
A general first-order initial value problem in ordinary differential equations relies heavily on a Lipschitz condition for its qualitative theory.
A function F satisfies the Lipschitz condition on a set D if there exists a non-negative constant L such that a specific inequality holds for all pairs of points in D.
The inequality associated with the Lipschitz condition dates back to Rudolf Lipschitz's 1876 paper and is fundamental to the study of functions involving one variable.
Verifying the Lipschitz condition can be straightforward in some cases, such as when the function and set D have a simple structure.
A lemma is presented that provides sufficient conditions under which a function F satisfies the Lipschitz condition, involving the continuity and boundedness of the partial derivative of F.
The proof of the lemma is based on the fundamental theorem of calculus, demonstrating the integral of the derivative of F.
Examples are given to illustrate the application of the lemma, including functions that do and do not satisfy the Lipschitz condition on specific sets.
The concept of convex sets is introduced as a generalization of rectangles and infinite strips, which are sets where the line segment between any two points remains within the set.
The Picard-Lindelöf theorem is mentioned, which guarantees the existence and uniqueness of a solution to an initial value problem if F satisfies a Lipschitz condition on a rectangle.
A corollary to the Picard-Lindelöf theorem is presented, which relates the existence and continuity of the partial derivative of F to the satisfaction of the Lipschitz condition.
The importance of checking the simpler conditions of the corollary for practical applications in ordinary differential equations is emphasized.
The presentation concludes with references to further reading on the topic of Lipschitz conditions and their role in the study of ordinary differential equations.
The use of Lipschitz conditions in proving the existence and uniqueness of solutions to initial value problems is a cornerstone in the theory of ordinary differential equations.
The presentation provides a clear understanding of how to verify whether a given function satisfies the Lipschitz condition and its implications for the study of differential equations.
The application of the fundamental theorem of calculus in proving the lemma related to the Lipschitz condition showcases the interconnection between different areas of mathematics.
The presentation highlights the practicality of the lemma by showing how easily one can compute the derivative of F and check for the satisfaction of the Lipschitz condition on a set of interest.
Transcripts
Browse More Related Video

Ordinary Differential Equations 9 | Lipschitz Continuity [dark version]

Ordinary Differential Equations 9 | Lipschitz Continuity

Ordinary Differential Equations 10 | Uniqueness for Solutions
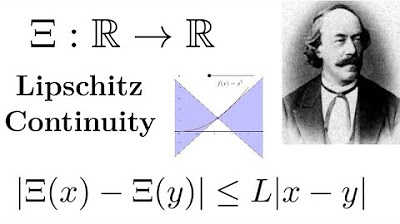
Intro to Lipschitz Continuity + Examples

Lipschitz functions

Lec 1 | MIT 18.03 Differential Equations, Spring 2006
5.0 / 5 (0 votes)
Thanks for rating: