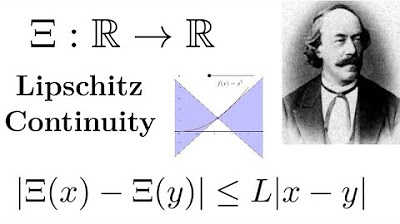Ordinary Differential Equations 9 | Lipschitz Continuity [dark version]
TLDRThis video from the Ordinary Differential Equations series delves into the concept of Lipschitz continuity, a crucial property for ensuring unique solutions to initial value problems in differential equations. The host begins by distinguishing Lipschitz continuity as a middle ground between continuity and differentiability, defining it for locally Lipschitz continuous functions. The formal definition is presented, emphasizing that it involves a local condition at each point within a domain, typically an epsilon ball in RN space. The video explains that Lipschitz continuity provides an estimate for the difference between two function values, with a constant L that bounds the rate of change within the local neighborhood. The host proves that a locally Lipschitz continuous function is also continuous and discusses its connection to differentiability, particularly for C1 functions. The mean value theorem is used to establish that the slopes of a differentiable function are bounded, which is a key property of Lipschitz continuity. The video concludes with the promise of applying these concepts to prove the uniqueness of solutions for initial value problems in the next installment.
Takeaways
- 📚 The video discusses the uniqueness of solutions for ordinary differential equations (ODEs), focusing on the concept of Lipschitz continuity.
- 🔍 Lipschitz continuity is a property that sits between continuity and differentiability, providing a middle ground necessary for solving ODEs uniquely.
- 🌟 A function is considered locally Lipschitz continuous if there exists a constant L such that the difference in the function's values is bounded by L times the difference in the input values within a local neighborhood.
- 📈 If a function is locally Lipschitz continuous, it is also continuous, as the convergence of input sequences implies the convergence of their function values.
- 🚫 Lipschitz continuity ensures that the slopes of a function within a neighborhood do not go to infinity, providing a bound on the rate of change.
- ➗ The mean value theorem can be applied to differentiable functions to show that the secant slope is less than or equal to a constant L, indicating Lipschitz continuity.
- 📉 For a continuously differentiable function (C1 function), the derivative provides an upper bound for the Lipschitz constant, making such functions locally Lipschitz continuous.
- 🧮 The concept of Lipschitz continuity is applicable in higher dimensions as well, which is significant for multidimensional ODEs.
- 📘 The video script outlines a proof that a C1 function is locally Lipschitz continuous, which is crucial for the study of ODEs.
- 🔑 The existence of a Lipschitz constant is key to ensuring the uniqueness of solutions to initial value problems in the context of ODEs.
- ➡️ The next video will apply these concepts to prove the uniqueness of solutions for initial value problems where the function is locally Lipschitz continuous.
Q & A
What is the main topic discussed in this video?
-The main topic discussed in this video is the uniqueness of solutions for ordinary differential equations, with a focus on the concept of Lipschitz continuity.
What does Lipschitz continuity represent in the context of functions?
-Lipschitz continuity represents a property of a function that is more than just continuity but less than being continuously differentiable. It ensures there is a bound on the rate of change of the function.
What is a locally Lipschitz continuous function?
-A function is locally Lipschitz continuous if, for every point in its domain, there exists a neighborhood where the function satisfies the Lipschitz condition with a constant L that is the same for all points within that neighborhood.
Why is Lipschitz continuity important for solving ordinary differential equations?
-Lipschitz continuity is important because it ensures the existence and uniqueness of solutions to ordinary differential equations, which is crucial for their analysis and application.
How does Lipschitz continuity relate to the differentiability of a function?
-If a function is locally Lipschitz continuous, it implies that the function's slopes are bounded, which in turn implies that the function is differentiable within the neighborhood where the Lipschitz condition holds.
What is the significance of the Lipschitz constant L in the context of Lipschitz continuity?
-The Lipschitz constant L provides an upper bound on the rate of change of the function within a given neighborhood. It is a crucial component in the definition of Lipschitz continuity and ensures that the function does not change too rapidly.
What does it mean for a function to be continuously differentiable?
-A function is continuously differentiable if it is differentiable at every point in its domain and its derivative is also a continuous function.
How does the mean value theorem apply to differentiable functions in the context of Lipschitz continuity?
-The mean value theorem states that for a differentiable function, the average rate of change (secant slope) over an interval is equal to the instantaneous rate of change (tangent slope) at some point within that interval. This helps establish that the slopes of the function are bounded, which is a requirement for Lipschitz continuity.
What is the implication of a function being C1?
-A function being C1 means it is continuously differentiable, which implies that it has a derivative that is itself a continuous function. This property often leads to the function also being locally Lipschitz continuous.
How does the concept of an epsilon neighborhood play a role in defining Lipschitz continuity?
-An epsilon neighborhood is used to define the local condition for Lipschitz continuity. It ensures that the Lipschitz condition holds for all points within a small neighborhood around a given point in the function's domain.
What is the role of the standard norm in measuring the difference between two values of a function in the context of Lipschitz continuity?
-The standard norm is used to measure the distance between the outputs of the function (V of Y and V of Z) and the distance between the inputs (Y and Z). This measurement is crucial for establishing the Lipschitz condition, which relates the rate of change of the function to the distance between its inputs.
Why is the uniqueness of solutions important for initial value problems in ordinary differential equations?
-The uniqueness of solutions is important because it guarantees that, given a specific initial condition, there is only one solution path that the system can follow. This is essential for making accurate predictions and for the practical application of the model.
Outlines
📘 Introduction to Lipschitz Continuity
The first paragraph introduces the concept of Lipschitz continuity, positioning it between the notions of continuity and differentiability. It explains that Lipschitz continuity is a property that a function possesses when there exists a constant that bounds the rate of change of the function's output with respect to changes in its input. The paragraph also establishes the importance of this property for solving ordinary differential equations (ODEs) uniquely. The formal definition of a locally Lipschitz continuous function is provided, emphasizing the local condition that must be met at each point within a neighborhood of the domain.
📙 Properties and Implications of Lipschitz Continuity
The second paragraph delves into the implications of a function being locally Lipschitz continuous. It proves that such a function is also ordinary continuous, using the convergence of a sequence of inputs to demonstrate the continuity of the function's images. The paragraph also explores the connection between Lipschitz continuity and differentiability, showing that the slopes of the function within a neighborhood are bounded by a constant. This property is crucial for the application to ODEs. The mean value theorem is used to establish that a continuously differentiable (C1) function is also locally Lipschitz continuous, providing a method to estimate the Lipschitz constant.
📗 Conclusion and Application to ODEs
The third paragraph concludes the discussion on Lipschitz continuity by stating that many examples of locally Lipschitz continuous functions can be found among differentiable functions. It highlights the significance of this property for the study of ODEs. The paragraph also hints at the application of these concepts in the next video, where it will be shown that for initial value problems with locally Lipschitz continuous functions, the solutions are unique. The video ends with a teaser for the upcoming content and a farewell note.
Mindmap
Keywords
💡Ordinary Differential Equations (ODEs)
💡Initial Value Problem
💡Lipschitz Continuity
💡Locally Lipschitz Continuous Functions
💡Continuity
💡Differentiability
💡Mean Value Theorem
💡Secant Slope
💡Tangent Slope
💡Lipschitz Constant
💡Uniqueness of Solutions
Highlights
The video discusses the uniqueness of solutions for ordinary differential equations (ODEs) with initial value problems.
Lipschitz continuity is identified as a key concept for ensuring unique solutions to ODEs.
Lipschitz continuity is positioned between the concepts of continuity and differentiability.
A function is defined as locally Lipschitz continuous if it satisfies a local condition at each point in its domain.
The definition of Lipschitz continuity involves a constant L that bounds the rate of change of the function's output with respect to changes in its input.
Local Lipschitz continuity implies ordinary continuity, ensuring that the function's output converges if the input does.
The slopes of the function's graph are bounded within a local neighborhood, a property derived from Lipschitz continuity.
Differentiable functions, particularly continuously differentiable (C1) functions, are shown to be locally Lipschitz continuous.
The Mean Value Theorem is used to establish the connection between differentiability and Lipschitz continuity.
For C1 functions, the derivative's supremum within an epsilon neighborhood can serve as the Lipschitz constant.
The video provides a proof that C1 functions are locally Lipschitz continuous, which is applicable to higher dimensions as well.
The concept of Lipschitz continuity is essential for the upcoming discussion on ordinary differential equations.
The video concludes with a teaser for the next video, which will cover the uniqueness of solutions for initial value problems with locally Lipschitz continuous functions.
The importance of the Lipschitz constant being well-defined and non-negative for the function's local behavior is emphasized.
The video acknowledges the support of patrons which enables the creation of mathematical content.
The concept of an epsilon ball is introduced as a tool to define the local nature of Lipschitz continuity.
The video explains that Lipschitz continuity is a stronger condition than simple continuity but less restrictive than continuous differentiability.
The video concludes with a reminder of the significance of Lipschitz continuity in the study of ODEs and its practical applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: