Examples identifying Type I and Type II errors | AP Statistics | Khan Academy
TLDRThe video script discusses the concept of Type I and Type II errors in statistical hypothesis testing. Using two scenarios, the first involves a mayor testing the unemployment rate in her town against a national average of 9%. The script explains that a Type I error occurs when the null hypothesis (unemployment rate equals 9%) is rejected despite being true. The second scenario involves a university considering building a new cafeteria based on student interest in a meal plan. A Type II error in this context would mean not building the cafeteria when there is actually a high demand (more than 40%), leading to insufficient space. The video emphasizes the importance of understanding these errors to avoid incorrect conclusions that contradict reality.
Takeaways
- 📊 A nationwide poll revealed a 9% unemployment rate in the U.S., prompting a local mayor to investigate if her town's rate is significantly different.
- 🎯 The mayor's null hypothesis (H0) is that the town's unemployment rate is the same as the national average (9%), while her alternative hypothesis (H1) is that it is different.
- 🚫 A Type I error occurs when the null hypothesis is incorrectly rejected even though it is true. In this context, it means concluding the town's rate is not 9% when it actually is.
- 🤔 To identify a Type I error, consider if the conclusion rejects a true null hypothesis; if so, it's a Type I error.
- 🏛️ In the mayor's case, a Type I error would mean she concludes the town's unemployment rate is not 9% when it is, leading to incorrect policy or decision-making.
- 🏢 A university is considering building a new cafeteria based on whether more than 40% of students are interested in a meal plan.
- 🍽️ The null hypothesis (H0) for the university is that 40% or fewer students are interested in a meal plan, while the alternative (H1) is that more than 40% are interested.
- 🛠️ A Type II error in this context would mean failing to reject the null hypothesis when it is false, leading to not building a new cafeteria when there is actually high demand.
- 🤷♂️ A correct decision would be not considering a new cafeteria when the proportion of interested students is indeed 40% or less, which is a true null hypothesis.
- 🏗️ A Type I error in the university scenario would be considering building a new cafeteria when the null hypothesis is true (i.e., when 40% or fewer students are interested).
- 📉 The consequences of a Type II error are missing out on opportunities, such as not building a new cafeteria when it's needed due to high student interest.
- 📈 Understanding the implications of Type I and Type II errors is crucial for making informed decisions in statistical analysis and hypothesis testing.
Q & A
What is the main concern of the mayor regarding the unemployment rate in her town?
-The mayor is concerned that the national unemployment rate of 9% might not be reflective of her town's actual unemployment rate and is considering a sample survey to determine if there's a significant difference.
What does the null hypothesis represent in the context of the mayor's survey?
-The null hypothesis represents the assumption that the unemployment rate in the mayor's town is the same as the national rate, which is 9%.
What is the alternative hypothesis in the mayor's survey?
-The alternative hypothesis is that the unemployment rate in the town is not the same as the national rate of 9%.
What is a Type I error in the context of statistical hypothesis testing?
-A Type I error occurs when the null hypothesis is rejected even though it is actually true. In the mayor's case, it would mean concluding that the town's unemployment rate is not 9% when it actually is.
What is a Type II error in the context of statistical hypothesis testing?
-A Type II error occurs when the null hypothesis is not rejected even though it is false. In the mayor's case, it would mean concluding that the town's unemployment rate is 9% when it is actually different.
What is the consequence of a Type I error in the mayor's survey?
-The consequence of a Type I error would be that the mayor might take unnecessary actions or make incorrect decisions based on the belief that the unemployment rate is different from the national average, when it is not.
What is the consequence of a Type II error in the mayor's survey?
-The consequence of a Type II error would be that the mayor might miss out on addressing a real issue, such as a higher unemployment rate in the town that requires attention and intervention.
Why is the university considering building another cafeteria?
-The university is considering building another cafeteria because they want to determine if there is strong evidence that the proportion of students interested in a meal plan is higher than 40%.
What is the null hypothesis for the university's survey about the meal plan?
-The null hypothesis for the university's survey is that 40% or fewer students are interested in a meal plan.
What is the alternative hypothesis for the university's survey about the meal plan?
-The alternative hypothesis is that more than 40% of the students are interested in a meal plan.
What is the consequence of a Type II error in the context of the university's cafeteria survey?
-The consequence of a Type II error would be that the university does not consider building a new cafeteria when they should, potentially leading to insufficient cafeteria space for the students who are interested in a meal plan.
What is the consequence of a Type I error in the context of the university's cafeteria survey?
-The consequence of a Type I error would be that the university considers building a new cafeteria when it is not necessary, as the actual interest in a meal plan may be 40% or less.
Outlines
📊 Understanding Type I Error in Unemployment Rate Analysis
The first paragraph discusses the concept of a Type I error in the context of a nationwide poll showing a 9% unemployment rate in the United States. A local mayor is interested in whether this rate applies to her town and plans to conduct a sample survey. The null hypothesis (P) is that the town's unemployment rate is the same as the national average (9%), while the alternative hypothesis suggests it is different. A Type I error would occur if the mayor concludes that the town's unemployment rate is not 9% when it actually is. The paragraph explains that rejecting a true null hypothesis is a Type I error and contrasts it with a Type II error, which is failing to reject a false null hypothesis. The correct answer to the mayor's scenario is identified, and additional examples are provided to solidify the concept.
🏢 Implications of a Type II Error in University Cafeteria Planning
The second paragraph explores the consequences of a Type II error using the example of a university considering the construction of an additional cafeteria based on student interest in a meal plan. The null hypothesis is that 40% or fewer students are interested in a meal plan, while the alternative hypothesis is that more than 40% are interested. A Type II error in this scenario would mean that the university fails to recognize that more than 40% of students are interested in a meal plan and, therefore, does not build a new cafeteria when they should. The paragraph outlines the potential outcomes of both Type I and Type II errors in this context, emphasizing the importance of correctly interpreting statistical results to make informed decisions.
Mindmap
Keywords
💡Unemployment Rate
💡Nationwide Poll
💡Sample
💡Hypotheses
💡Type I Error
💡Type II Error
💡Null Hypothesis
💡Alternative Hypothesis
💡Statistical Significance
💡Proportion
💡Meal Plan
💡Error Types
Highlights
A large nationwide poll shows an unemployment rate of 9% in the United States.
The mayor of a local town plans to sample her residents to see if the unemployment rate in her town differs from the national average.
Let P represent the unemployment rate in the town, with null hypothesis that it is the same as the national rate, and alternative hypothesis that it is different.
A Type I error occurs when the null hypothesis is rejected even though it is true.
The mayor would commit a Type I error if she concludes the town's unemployment rate is not 9% when it actually is.
Rejecting the null hypothesis when it is true is considered doing something that contradicts reality.
The mayor's decision to reject or not reject the null hypothesis is based on whether the unemployment rate is actually 9% or not.
A Type II error is when the null hypothesis is not rejected even though it is false.
A large university is considering building another cafeteria based on student interest in a meal plan.
The null hypothesis is that 40% or fewer students are interested in a meal plan, with the alternative being more than 40%.
A Type II error in this context would mean not considering building a new cafeteria when they should.
Failing to reject a false null hypothesis leads to incorrect conclusions about the proportion of students interested in a meal plan.
The consequence of a Type II error could result in insufficient cafeteria space for the student population.
Correct conclusions are made when the null hypothesis is not rejected when it is true (Type II error) or when it is rejected when it is false (Type I error).
Considering building a new cafeteria when the null hypothesis is true would be a Type I error.
The decision to build a new cafeteria should be based on accurate statistical analysis to avoid Type I and Type II errors.
Understanding the implications of Type I and Type II errors is crucial for making informed decisions in statistical hypothesis testing.
Transcripts
Browse More Related Video

Introduction to Type I and Type II errors | AP Statistics | Khan Academy

Type I error vs Type II error

Errors and Power in Hypothesis Testing | Statistics Tutorial #16 | MarinStatsLectures

How To Identify Type I and Type II Errors In Statistics

Type 1 errors | Inferential statistics | Probability and Statistics | Khan Academy
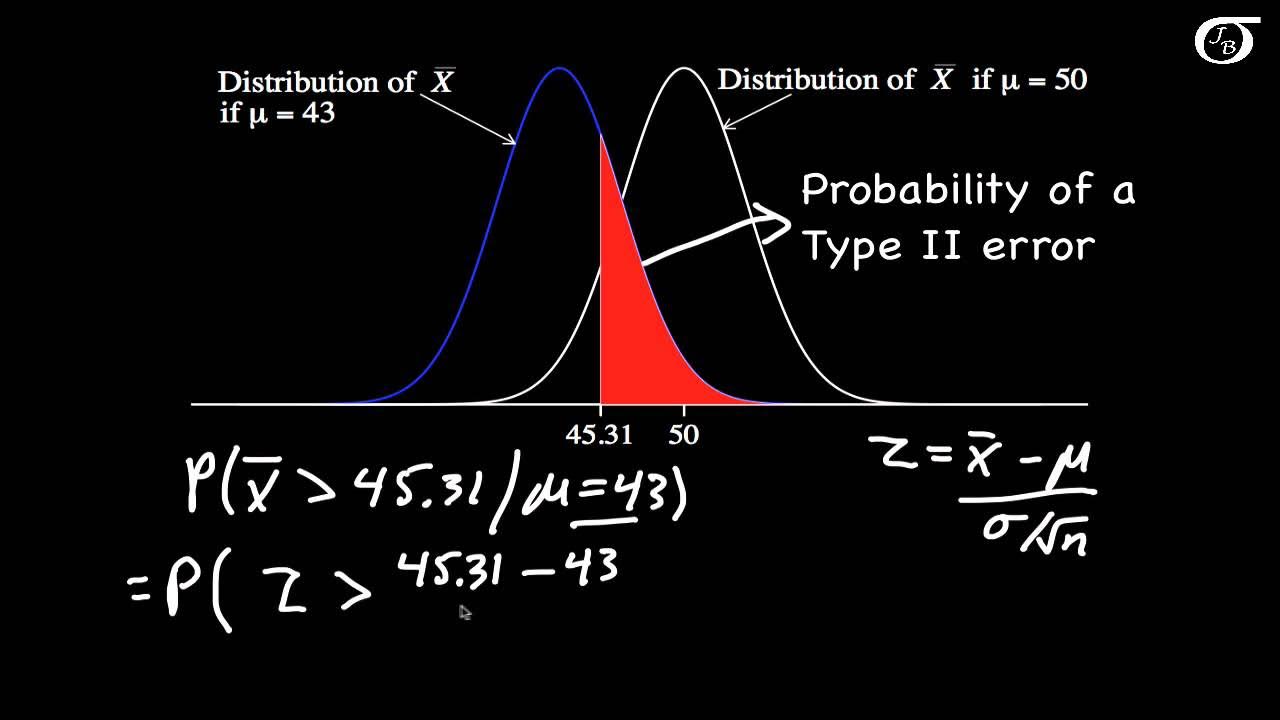
Calculating Power and the Probability of a Type II Error (A One-Tailed Example)
5.0 / 5 (0 votes)
Thanks for rating: