p-hacking: What it is and how to avoid it!
TLDRIn this engaging StatQuest video, host Josh explains the concept of P-hacking, a practice where statistical analysis is misused, leading to false positives. He illustrates this through an example of testing drugs for virus recovery, emphasizing the importance of not cherry-picking data. Josh introduces the multiple testing problem and suggests using the false discovery rate to adjust p-values and reduce false positives. He also warns against adding more data to a test just to achieve statistical significance, which is another form of P-hacking. To prevent this, he recommends conducting a power analysis before an experiment to determine the appropriate sample size. The video concludes with a call to action for viewers to subscribe and support the channel.
Takeaways
- 📉 **P-Hacking Definition**: P-hacking refers to the misuse and abuse of statistical analysis techniques which can lead to false positives.
- 🔍 **Understanding P-Values**: The video assumes familiarity with p-values, which are used to determine if results are statistically significant.
- ☠️ **Risk of False Positives**: Using a significance threshold of 0.05 means about 5% of tests will yield false positives when data comes from the same distribution.
- 📈 **Multiple Testing Problem**: Performing many tests increases the likelihood of encountering false positives, which is known as the multiple testing problem.
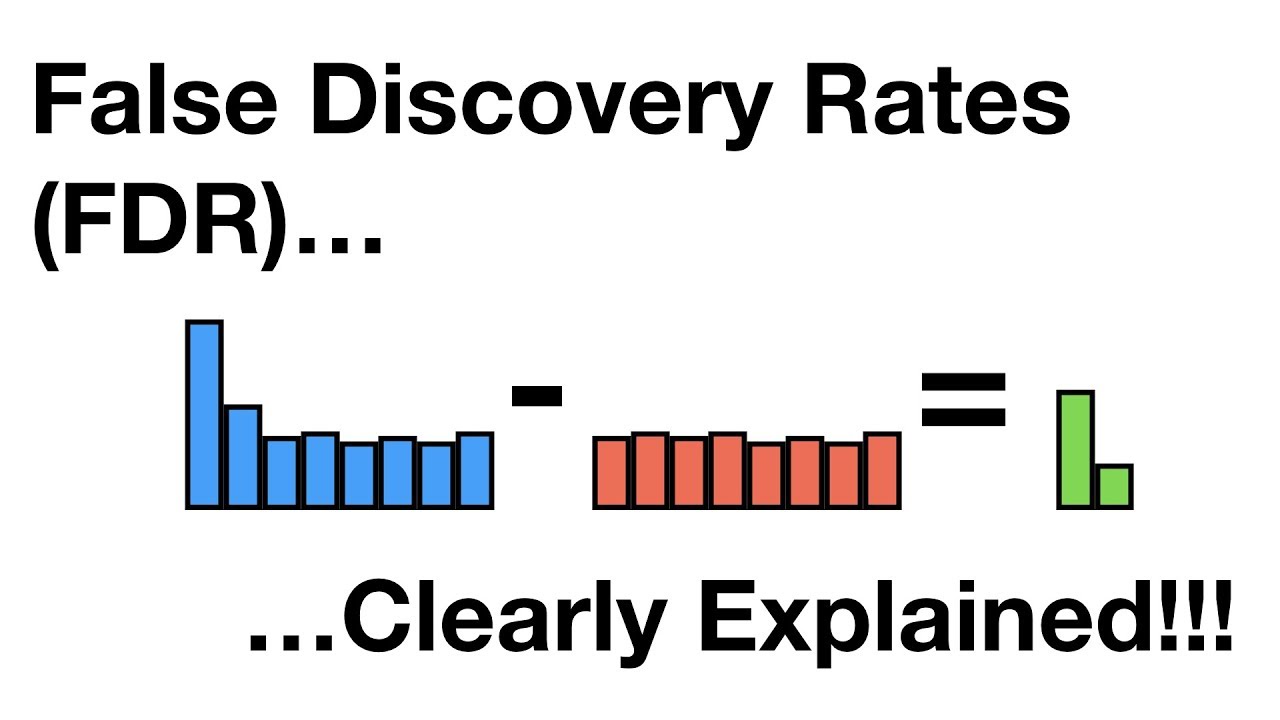
- 🛠️ **False Discovery Rate (FDR)**: A method to adjust p-values to account for multiple comparisons, which can help reduce the number of false positives.
- 🚫 **Avoid Cherry-Picking**: Do not select only favorable results for testing; include all p-values to avoid biased outcomes.
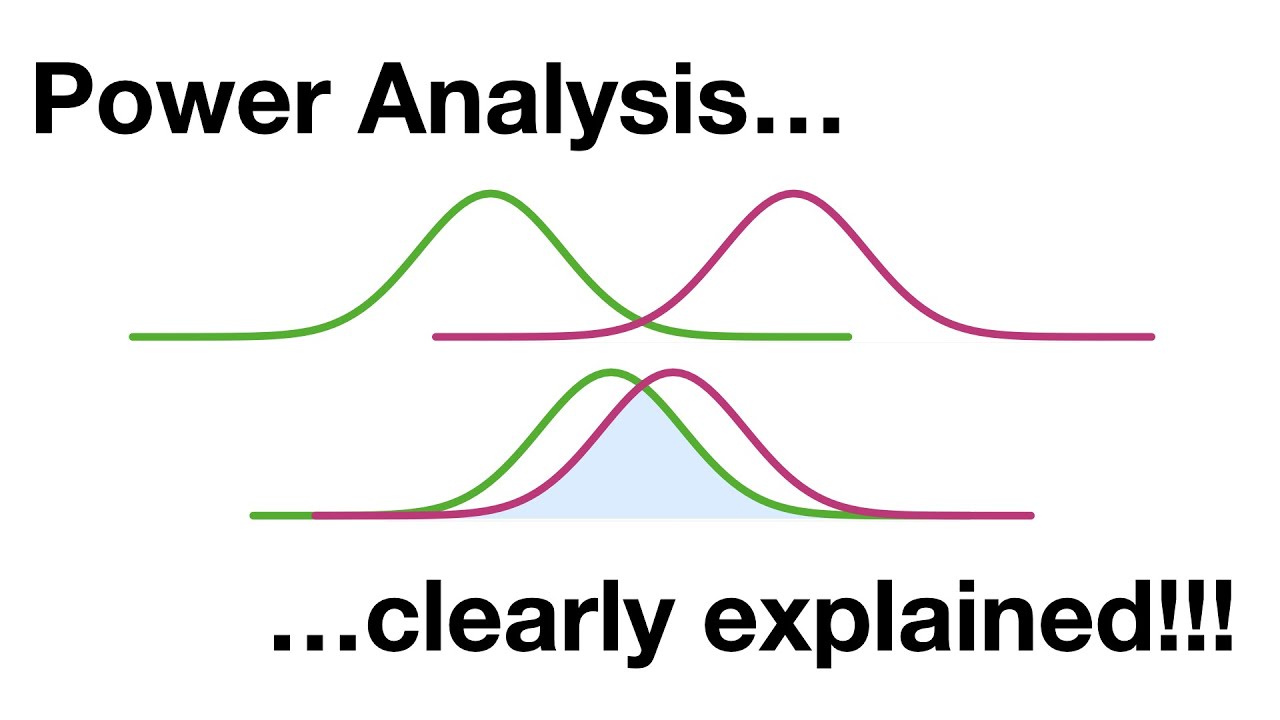
- 🔮 **Power Analysis**: Conducted before an experiment to determine the necessary sample size to have a high probability of correctly rejecting the null hypothesis.
- 📊 **Sample Size Importance**: Knowing the correct sample size is crucial to avoid false positives and ensure the reliability of experimental results.
- 🔄 **Adding Data Caution**: Adding more data to a test with a p-value close to 0.05 increases the risk of obtaining a false positive result.
- 🧐 **Awareness of Distribution**: In experiments, it's often unknown if data comes from the same or different distributions, which should be considered when analyzing results.
- ✅ **Proper Experimental Design**: To avoid p-hacking, use proper experimental design that includes determining the correct sample size and adjusting for multiple testing.
- 📚 **Further Learning**: The speaker encourages viewers to seek more information on power analysis and other statistical methods to improve experimental outcomes.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is P-hacking, which is the misuse and abuse of statistical analysis techniques that can lead to false positives in research.
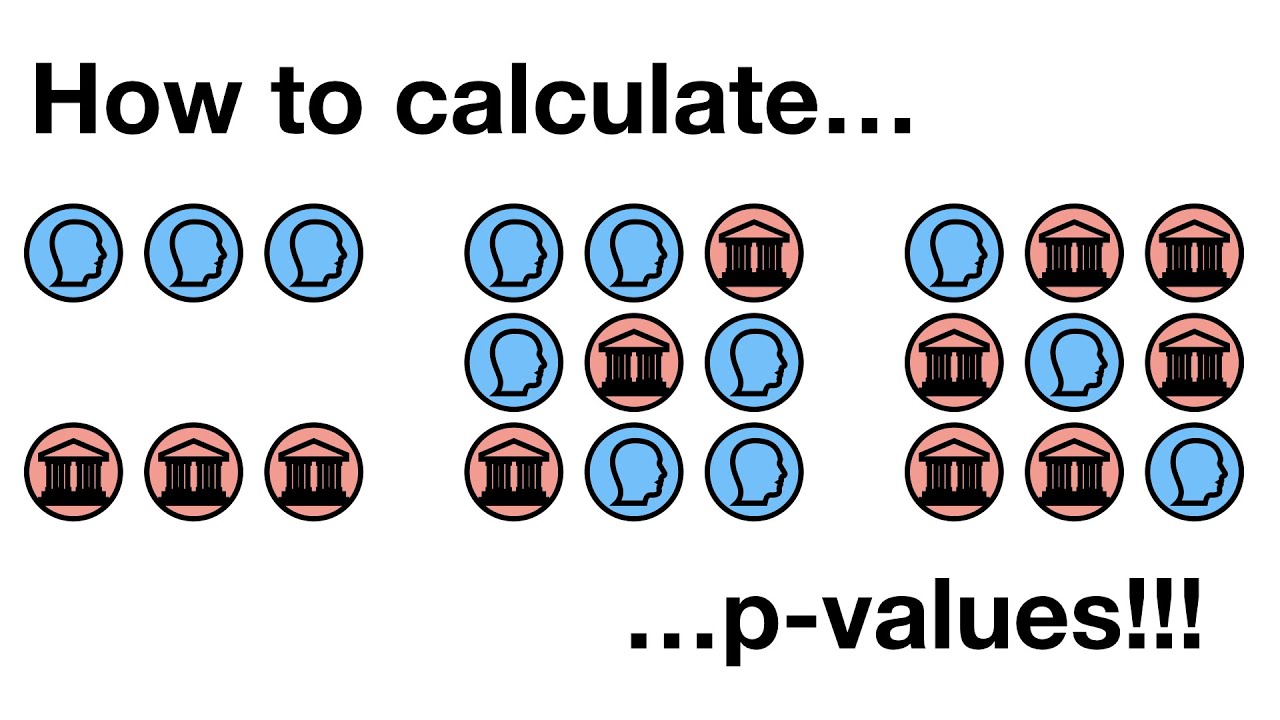
What is the significance of a p-value in statistical testing?
-A p-value is used to determine the probability that the observed results occurred by chance under the null hypothesis. A commonly used threshold is 0.05; if the p-value is less than this, the null hypothesis is rejected, indicating a statistically significant result.
Why is P-hacking considered a problem in research?
-P-hacking is a problem because it can lead to false positives, where researchers mistakenly conclude that there is a significant effect or difference when there is not. This can mislead scientific understanding and practice.
What is the 'multiple testing problem'?
-The multiple testing problem arises when numerous statistical tests are conducted on the same dataset. The more tests that are done, the higher the chance of encountering false positives due to the increased probability of purely random results crossing the significance threshold.
How can the false discovery rate (FDR) help address the multiple testing problem?
-The false discovery rate is a method that adjusts p-values from multiple tests to control the expected proportion of false positives among the rejected hypotheses. It helps reduce the number of false positives by applying a more stringent threshold to each test.
What is the role of a power analysis in avoiding P-hacking?
-A power analysis is performed before conducting an experiment to determine the appropriate sample size. It helps ensure that there is a high probability of correctly rejecting the null hypothesis if there is a true effect, thus preventing the researcher from being misled by false positives.
Why should researchers not only test the data that looks most promising?
-Researchers should not cherry-pick data because it introduces bias and can lead to P-hacking. All data should be included in the analysis to maintain the integrity of the results and to accurately assess the significance of findings.
What is the null hypothesis in the context of the drug testing example?
-In the drug testing example, the null hypothesis is that there is no difference in recovery time between individuals who take a specific drug and those who do not. Rejecting the null hypothesis would suggest that the drug has a significant effect on recovery time.
How can a researcher ensure that they are not adding observations to a dataset just to achieve a statistically significant result?
-To avoid this, a researcher should conduct a power analysis beforehand to determine the necessary sample size. Additionally, they should not continue to add data until a significant result is achieved but rather stick to the predetermined sample size and analysis plan.
What is the consequence of not correcting for multiple comparisons in a statistical analysis?
-Not correcting for multiple comparisons can lead to an inflated rate of false positives, as the probability of finding at least one significant result by chance increases with the number of comparisons made.
Why is it important to include all p-values from all tests when using methods that compensate for multiple testing?
-Including all p-values ensures that the adjustments for multiple testing are accurate and that the final results are not skewed by selective reporting. It helps maintain the integrity of the statistical analysis and reduces the risk of false positives.
What does the video suggest for a researcher to do when they get a p-value that is close to, but not less than, 0.05?
-Instead of adding more data to the existing dataset to force a significant result, the video suggests conducting a power analysis to determine the correct sample size. This approach is more scientifically rigorous and helps avoid false positives.
Outlines
😀 Understanding P-Hacking and Its Pitfalls
The first paragraph introduces the concept of p-hacking, which is the misuse and abuse of statistical analysis techniques that can lead to false positives. It uses the analogy of testing drugs to combat a virus to illustrate how p-values are calculated and interpreted. The importance of not falling for the allure of a low p-value without proper context is emphasized. The paragraph also explains the concept of a normal distribution and how it applies to recovery times in a hypothetical drug trial. The key takeaway is the danger of p-hacking and the necessity to understand and avoid it to ensure the validity of statistical tests.
🔍 The Multiple Testing Problem and False Discovery Rate
The second paragraph delves into the multiple testing problem, which occurs when conducting numerous statistical tests increases the likelihood of encountering false positives. It explains that a p-value threshold of 0.05 means that 5% of tests will yield false positives when the null hypothesis is true. The paragraph introduces the false discovery rate (FDR) as a method to adjust p-values and reduce false positives. It also cautions against cherry-picking data to achieve a desired outcome and stresses the importance of including all test results in the analysis. The FDR method is presented as a way to compensate for multiple testing and maintain the integrity of statistical findings.
📉 Power Analysis and Avoiding P-Hacking in Practice
The third paragraph discusses the practice of p-hacking in experimental design and the temptation to add more data points to achieve a statistically significant result. It warns against this practice, especially when the initial p-value is close to the significance threshold, as it can lead to false positives. The solution proposed is to conduct a power analysis before the experiment to determine the appropriate sample size, ensuring a high probability of correctly rejecting the null hypothesis if it is false. The paragraph concludes with a summary of best practices for testing multiple hypotheses, emphasizing the importance of adjusting p-values for multiple comparisons and using power analysis to prevent false positives.
Mindmap
Keywords
💡P hacking
💡P-value
💡Null Hypothesis
💡False Positive
💡Multiple Testing Problem
💡False Discovery Rate (FDR)
💡Cherry-Picking
💡Power Analysis
💡Sample Size
💡Statistical Significance
💡Normal Distribution
Highlights
P-hacking is the misuse and abuse of statistical analysis techniques that can lead to false positives.
A p-value of 0.02 led to the rejection of the null hypothesis for Drug II, which appeared effective, but this could be a result of p-hacking.
The concept of p-hacking involves the risk of being misled by false positives, which can occur even when the p-value threshold is set at 0.05.
When multiple tests are conducted, the likelihood of false positives increases, a problem known as the multiple testing problem.
The false discovery rate (FDR) is a method to adjust p-values and reduce the number of false positives in multiple testing scenarios.
To properly apply the FDR or other methods compensating for multiple testing, all p-values from all tests should be included, not just those indicating significance.
Cherry-picking data to achieve a small p-value is a form of p-hacking that should be avoided.
When experiments are conducted without prior knowledge of the distribution, it's tempting to add more data to achieve significance, which can lead to p-hacking.
Adding more measurements to a dataset with a p-value close to 0.05 increases the risk of a false positive.
A power analysis should be performed prior to an experiment to determine the appropriate sample size and avoid false positives.
The video emphasizes the importance of not only looking at data that appears significant post-experiment but conducting a proper power analysis beforehand.
The use of a p-value threshold of 0.05 assumes that only a single p-value is calculated for decision-making, which is not the case in practice.
The video explains that conducting multiple tests on the same dataset and adjusting p-values accordingly can help prevent false positives.
The concept of p-hacking is further explored through the example of testing various drugs for their effectiveness against a virus.
The video concludes with a call to action for viewers to subscribe for more content and support the channel through Patreon or merchandise.
The importance of understanding and avoiding p-hacking is emphasized to ensure the integrity and reliability of statistical analyses in research.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: