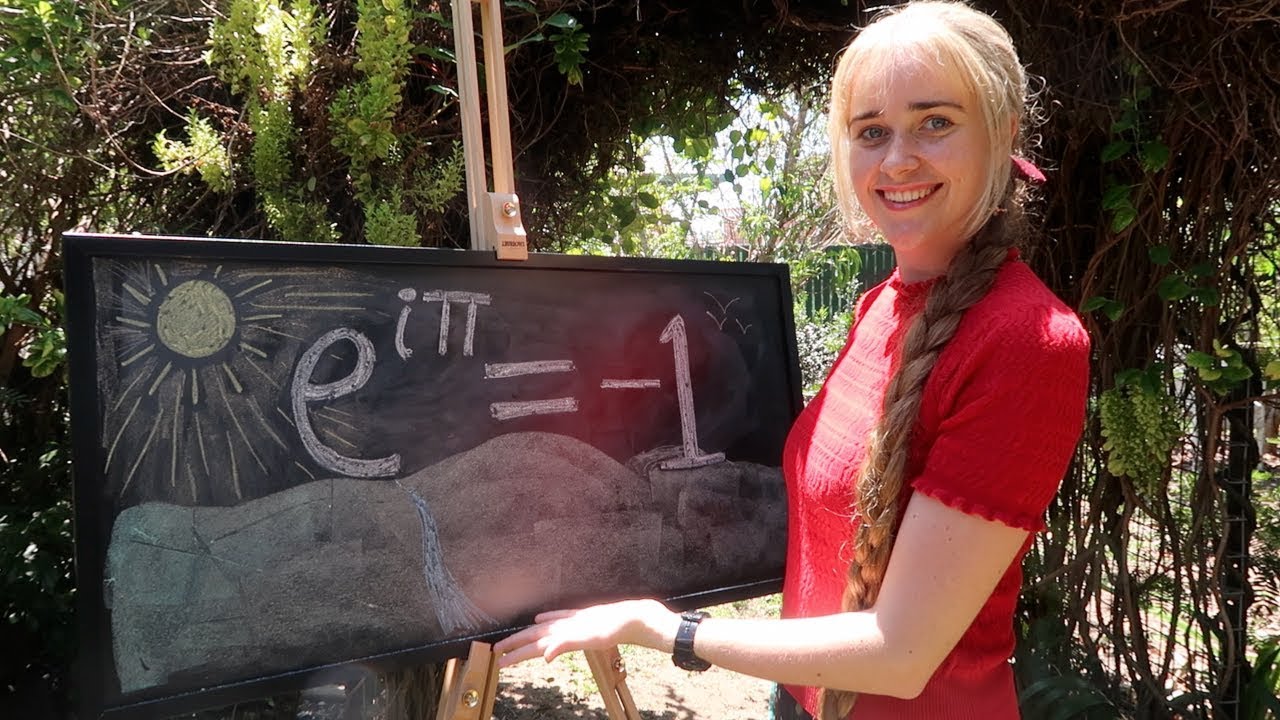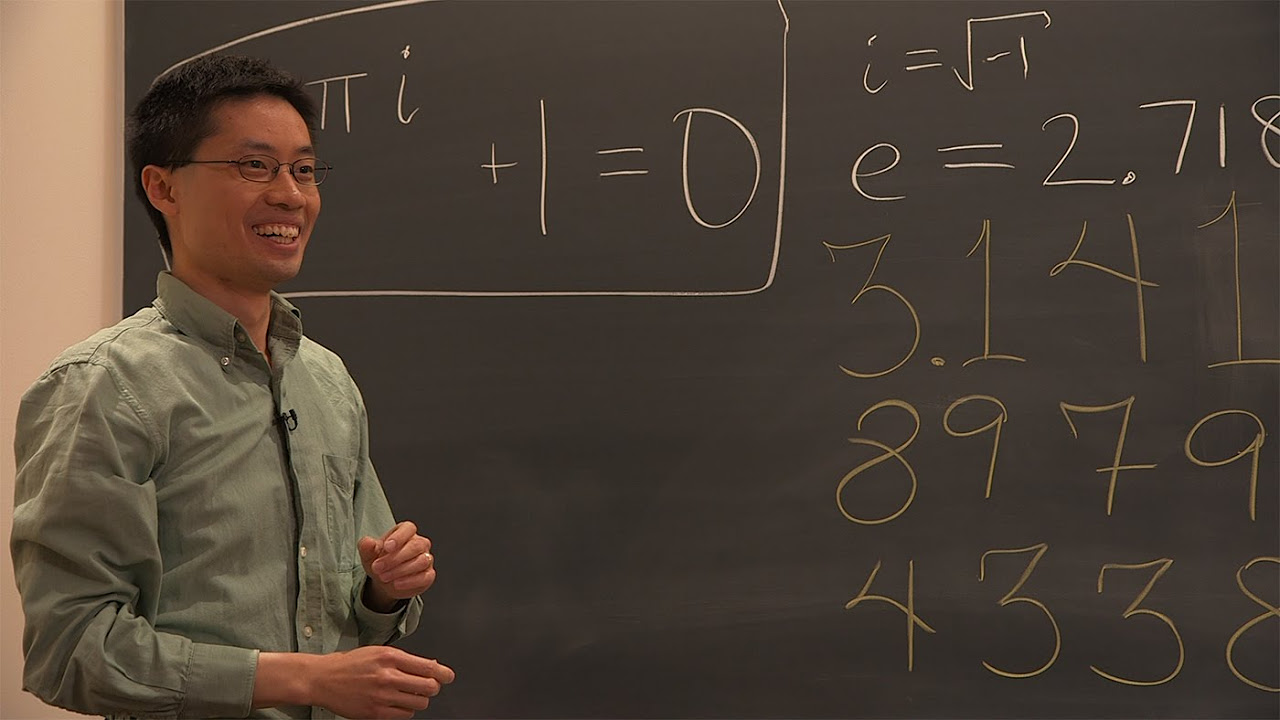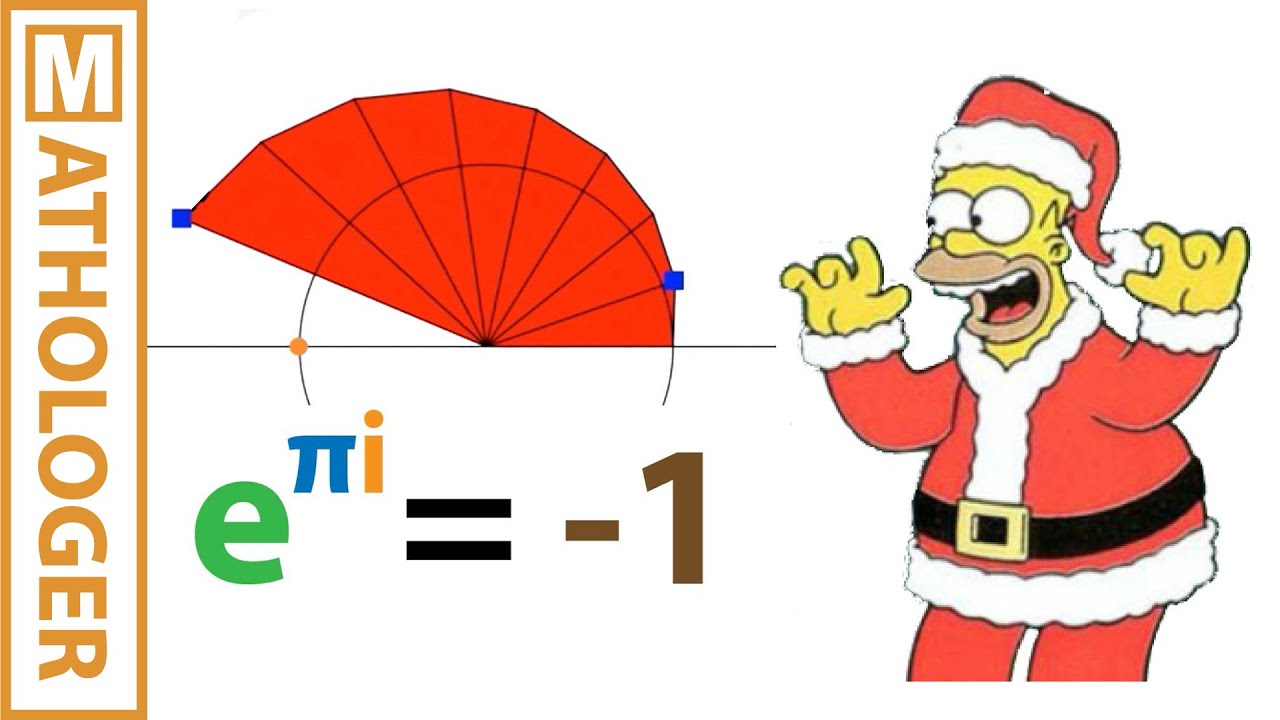Polynomial approximation of functions (part 7)
TLDRThe video script delves into the fascinating relationship between the imaginary unit 'i', Euler's formula, and trigonometric functions. It explains how 'i' can be treated similarly to real numbers when used in polynomials, leading to the discovery that e to the power of 'i x' equals cosine of 'x' plus 'i' times sine of 'x'. The script further explores the profound implications of Euler's formula, culminating in the remarkable revelation that e to the power of 'i pi' equals -1, highlighting an unexpected convergence of fundamental mathematical constants from diverse origins.
Takeaways
- 🌟 The concept of 'i' and its sign changes are closely related to the Maclaurin representation of cosine and sine functions.
- 🔍 The idea of raising anything to the 'i' power was initially undefined, but through exploration, it was found to relate to trigonometric functions.
- 🧠 Euler's formula, e^(ix) = cos(x) + i*sin(x), establishes a profound connection between the numbers e, i, and fundamental trigonometric functions.
- 📈 By substituting 'x' with 'ix' in the Maclaurin series of e^x, one can derive the expression for e^(ix), highlighting the role of polynomial roots in the definition of 'i'.
- 🌐 When x is replaced with pi in Euler's formula, e^(iπ) equals -1, revealing a surprising relationship between 'e', 'i', and 'π'.
- 🤔 The script emphasizes the mysterious and almost mystical nature of mathematical concepts like 'e', 'i', and 'π', which come from different areas of mathematics yet are interconnected.
- 📊 The Maclaurin series for e^x allows for the derivation of the Maclaurin series for both cosine and sine functions by separating real and imaginary terms.
- 🔧 The process of understanding e^(ix) can be seen as an experiment in mathematics, showcasing the iterative and exploratory nature of mathematical discovery.
- 🌀 The sign changes of 'i' and the corresponding sine terms illustrate the intricate relationships within mathematical functions and their representations.
- 📖 The script serves as a reminder of the beauty and complexity of mathematics, where fundamental concepts can lead to awe-inspiring revelations.
- 🌈 The discussion of e^(ix) and its relation to trigonometric functions is a testament to the power of mathematical representation and the ability to make connections between seemingly disparate ideas.
Q & A
What is the significance of the pattern of sign changes in relation to the Maclaurin representation of cosine and sine functions?
-The pattern of sign changes in the Maclaurin representation of cosine and sine functions is significant because it mirrors the behavior of the imaginary unit 'i'. This observation leads to the formulation of Euler's formula, which establishes a deep connection between these mathematical concepts.
How is 'i' defined in the context of the script?
-In the script, 'i' is defined as the imaginary unit where 'i' squared equals negative 1. This definition is fundamental for understanding complex numbers and their properties.
What is the Maclaurin representation, and how does it relate to the function e^x?
-The Maclaurin representation is a series representation of a function as a power series at a specific point, in this case, x=0. It relates to the function e^x by providing an approximation of the exponential function using a polynomial, which is particularly useful for finding roots of polynomials without real roots.
What does the script imply about the relationship between 'i' and the sine function?
-The script implies that 'i' is closely related to the sine function in the sense that when 'i' is raised to different powers, it corresponds to the sine terms in the Maclaurin representation of the functions involved.
How does the script demonstrate the derivation of Euler's formula?
-The script demonstrates the derivation of Euler's formula by showing that e^(i*x) can be expressed as a sum of real and imaginary terms, which correspond to the cosine and sine functions, respectively. This leads to the conclusion that e^(i*x) = cos(x) + i*sin(x), which is Euler's formula.
What is the significance of e^(i*pi) in the context of Euler's formula?
-The significance of e^(i*pi) in Euler's formula is that it simplifies to -1, which is a profound result showing the interplay between the fundamental numbers e, i, and pi, and revealing an unexpected property of these mathematical constants.
How does the script connect the concepts of complex numbers, trigonometry, and fundamental mathematical constants?
-The script connects these concepts by exploring the properties of 'i' and its relation to the trigonometric functions sine and cosine. It then uses this relationship to derive Euler's formula, which encapsulates the interconnection between complex numbers, trigonometry, and fundamental constants like e and pi.
What is the role of the Maclaurin representation in the derivation of Euler's formula?
-The Maclaurin representation plays a crucial role in the derivation of Euler's formula by providing a series expansion of the exponential function e^x. This expansion allows for the substitution of 'i*x' into the series, leading to the separation of real and imaginary terms and the eventual formulation of Euler's formula.
What does the script suggest about the nature of mathematical truths?
-The script suggests that mathematical truths, such as those embodied in Euler's formula, can be both profound and mysterious. While they can be proven and are consistent within the framework of mathematics, their deeper meaning and why they hold true may not be fully understood, even by the most knowledgeable mathematicians.
How does the script use the concept of 'i' to bridge the gap between algebra and trigonometry?
-The script uses the concept of 'i' to bridge algebra and trigonometry by showing that the powers of 'i' correspond to the terms in the Maclaurin representation of sine and cosine functions. This connection allows for the development of Euler's formula, which unifies these two areas of mathematics.
What is the practical implication of Euler's formula in mathematics?
-Euler's formula has practical implications in mathematics as it provides a powerful tool for simplifying and analyzing complex exponential functions. It also enables the manipulation of complex numbers in a more intuitive way and has applications in various fields such as engineering, physics, and computer science.
Outlines
🔢 Mathematical Intuition and Euler's Formula
This paragraph delves into the mathematical intuition behind the sign changes of 'i' and its relation to the Maclaurin representation of cosine and sine functions. It introduces the concept of raising 'e' to the power of 'i' and explains how, despite the lack of a formal definition for this operation, one can treat 'i' like any other number for the sake of exploration. The discussion leads to the derivation of 'e^(i*x)' by substituting 'x' with 'i*x' in the Maclaurin series for 'e^x'. The result is a series that closely resembles the expressions for sine and cosine functions, with the presence of 'i' introducing an imaginary component. The paragraph concludes with the assertion that 'e^(i*x)' can be expressed as a combination of cosine and sine functions, highlighting the significance of Euler's formula in connecting these fundamental mathematical concepts.
📊 Separating Real and Imaginary Components in Euler's Formula
This paragraph focuses on the separation of real and imaginary terms in the expression derived from Euler's formula. It explains how the real terms are related to the cosine function and the imaginary terms to the sine function. The speaker clarifies the Maclaurin representations of both cosine and sine functions and establishes their equivalence to the corresponding terms in the expression for 'e^(i*x)'. The paragraph culminates in the revelation of Euler's formula, 'e^(i*pi) = -1', which elegantly links the fundamental numbers 'e', 'i', and 'pi', and underscores the profound implications of this relationship in the field of mathematics.
🌌 The Mysterious Order in the Universe
The final paragraph reflects on the profound and enigmatic nature of the mathematical relationships discovered in the previous sections. It emphasizes the remarkable convergence of distinct mathematical concepts—'e' from continuous compound interest, 'i' as the square root of negative one, and 'pi' as the ratio of a circle's circumference to its diameter—in Euler's formula. The speaker suggests that this formula offers a glimpse into an underlying order in the universe, which may not be fully comprehended by humanity. The paragraph leaves the audience with a sense of awe and curiosity about the interconnectedness of fundamental mathematical elements.
Mindmap
Keywords
💡Maclaurin representation
💡Sign changes
💡Exponential function
💡Complex numbers
💡Trigonometric functions
💡Euler's formula
💡Imaginary unit 'i'
💡Polynomials
💡Derivatives
💡Factorial
💡Cosine and Sine
💡Pi
Highlights
The pattern of sign changes in 'i' is similar to the Maclaurin representation of cosine of x plus sine of x.
Positive and negative 'i's correspond to the sine terms.
Euler's formula, e^(ix) = cos(x) + i*sin(x), is derived from the Maclaurin series.
The Maclaurin representation of e^(x) can be applied to e^(ix) by replacing x with ix.
The real terms of e^(ix) represent the cosine function, and the imaginary terms represent the sine function.
The Maclaurin representation of e^(ix) simplifies to 1 - x^2/2! + x^4/4! - x^6/6! and so on for the real part.
The imaginary part of e^(ix) is i*(x - x^3/3! + x^5/5! - x^7/7!) and continues to infinity.
Euler's formula connects the numbers e, i, and pi, which are fundamental in mathematics but come from different areas.
The formula e^(i*pi) = -1 is a profound result showing the interconnection of fundamental mathematical constants.
The derivation of Euler's formula demonstrates the power of mathematical definitions and the Maclaurin series.
The concept of raising a number to the power of 'i' was initially undefined but was explored through analogy.
The leap of faith in treating 'i' like any other number led to the discovery of Euler's formula.
The Maclaurin representation of e^(x) was used as a basis for exploring e^(ix).
The sign changes in the power of 'i' were crucial in deriving the relationship with trigonometric functions.
The formula e^(ix) showcases the beauty of mathematics in its ability to connect seemingly unrelated concepts.
The exploration of e^(ix) and its relation to cosine and sine functions is an example of the experimental nature of mathematical discovery.
The derivation of Euler's formula is a testament to the human ability to find order and structure in the universe.
The fact that e^(ix) can be expressed as a combination of real and imaginary parts is a key insight into its properties.
The ability to rewrite e^(ix) as separate real and imaginary terms is a significant mathematical simplification.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: