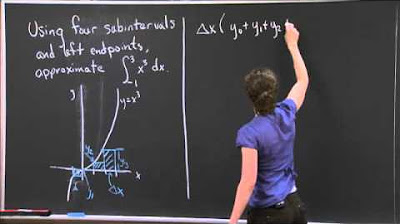Left, Right, & Midpoint Riemann Sum Formulas
TLDRThis video script offers an insightful explanation of Riemann sums, a method used to approximate the area under a curve by dividing it into rectangles. The presentation covers the three types of Riemann sums: left, right, and midpoint. The left Riemann sum uses the left endpoint of each subinterval to determine the height of the rectangles, while the right Riemann sum uses the right endpoint. The midpoint Riemann sum, however, employs the average value of the endpoints to establish the height. The script breaks down the mathematical formulas associated with each method, emphasizing the importance of understanding the conceptual basis behind the formulas. The video aims to clarify the terminology and notation, and provides a visual representation to enhance comprehension. It concludes by encouraging viewers to use the explanation as a reference for understanding Riemann sums.
Takeaways
- 📐 **Riemann Sums Overview**: The video discusses the formulas for left, right, and midpoint Riemann sums, which are used to approximate the area under a curve using rectangles.
- 📈 **Function and Interval**: The process involves a function f(x) and an interval [A, B], where the area under the curve is approximated by summing the areas of rectangles.
- 🟩 **Rectangle Width (Δx)**: The width of each rectangle (Δx) is determined by dividing the interval length (B - A) by the number of rectangles (n).
- 🔵 **Indexed X Values (X_i)**: The x-values used for the endpoints of the rectangles are indexed as X_i, representing the points where the function value is taken to determine the height of the rectangles.
- 🏗️ **Area Calculation**: The area of each rectangle is found by multiplying the height (f(X_i)) by the width (Δx), and these are summed up to approximate the total area.
- 🔠 **Left Riemann Sum**: For the left Riemann sum, the height of each rectangle is determined by the function value at the left endpoint of the interval.
- 🔄 **Right Riemann Sum**: In contrast, the right Riemann sum uses the function value at the right endpoint of each interval to determine the height of the rectangles.
- 🎯 **Midpoint Riemann Sum**: The midpoint Riemann sum uses the average of the function values at the endpoints of each interval to determine the height of the rectangles.
- 🌀 **Notation and Formulas**: The video emphasizes understanding the conceptual basis behind the mathematical notation and formulas for each type of Riemann sum.
- 📊 **Summation Convention**: The summation process is represented by a sum notation, which is particularly useful when dealing with a large number of rectangles.
- 📌 **Endpoints and Midpoints**: The choice between left, right, or midpoint Riemann sums depends on which points (endpoints or midpoints) are used to determine the height of the rectangles.
- 📚 **Educational Value**: The video serves as a reference for understanding the conceptual framework of Riemann sums and the reasoning behind their formulas.
Q & A
What are the three types of Riemann sums discussed in the video?
-The three types of Riemann sums discussed are the left Riemann sum, the right Riemann sum, and the midpoint Riemann sum.
How does the width of each rectangle in a Riemann sum relate to the interval and the number of rectangles?
-The width of each rectangle, denoted as Delta X, is found by taking the length of the interval (B - A) and dividing it by the number of rectangles (n).
What is the general formula for the area of a rectangle in the context of Riemann sums?
-The general formula for the area of a rectangle in Riemann sums is the height (f(X_sub_I)) multiplied by the width (Delta X).
How does the left Riemann sum determine the height of the rectangles?
-In the left Riemann sum, the height of each rectangle is determined by the function value at the left endpoint of the corresponding subinterval.
What is the difference between the left and right Riemann sums in terms of the height of the rectangles?
-The difference is that in the left Riemann sum, the height of the rectangle is the function value at the left endpoint of the subinterval, while in the right Riemann sum, it is the function value at the right endpoint.
How does the midpoint Riemann sum calculate the height of the rectangles?
-In the midpoint Riemann sum, the height of the rectangle is determined by the function value at the midpoint of the subinterval, which is calculated as the average of the function values at the endpoints of the subinterval.
What is the notation used to represent the midpoint in the midpoint Riemann sum?
-The notation used to represent the midpoint in the midpoint Riemann sum is a bar over the variable, such as X_bar.
What is the formula for the midpoint Riemann sum?
-The formula for the midpoint Riemann sum is the sum from I=1 to n of f(X_sub_I_bar) times Delta X, where X_sub_I_bar is the midpoint of the interval.
What is the purpose of using Riemann sums to approximate the area under a curve?
-Riemann sums are used to approximate the area under a curve when finding the definite integral. They provide a way to break down the area into rectangles of equal width and sum their areas to estimate the total area under the curve.
How does the choice of left, right, or midpoint affect the approximation of the area under a curve?
-The choice affects the accuracy and potential overestimation or underestimation of the area. The left Riemann sum tends to underestimate, the right Riemann sum tends to overestimate, and the midpoint Riemann sum provides a more balanced approximation.
What is the significance of the indexing in the Riemann sum formulas?
-The indexing (I) in the Riemann sum formulas is significant because it represents the iteration over each subinterval to sum the areas of the rectangles, which allows for the approximation of the total area under the curve.
Why are the formulas for the left, right, and midpoint Riemann sums similar but not identical?
-The formulas are similar because they all involve summing the product of a function value and the width of the rectangles. They differ in how the height of the rectangles is determined (left endpoint, right endpoint, or midpoint), which leads to different starting points and endpoints in the summation.
Outlines
📐 Understanding Riemann Sums
This paragraph introduces the concept of Riemann sums, which are used to approximate the area under a curve using rectangles. The speaker explains the three types of Riemann sums: left, right, and midpoint. The focus is on the conceptual understanding of the formulas used to calculate these sums. The process involves dividing the interval [A, B] into n equal subintervals with width ΔX and calculating the height of each rectangle at the endpoints. The height is determined by the function value at the chosen points (left, right, or midpoint), and the area of each rectangle is found by multiplying the height by the width. The sum of these areas approximates the area under the curve.
📊 Calculating Left, Right, and Midpoint Riemann Sums
The second paragraph delves into the specifics of calculating the left, right, and midpoint Riemann sums. For the left Riemann sum, the height of each rectangle is determined by the function value at the left endpoint of the interval. The right Riemann sum uses the function value at the right endpoint instead. The midpoint Riemann sum calculates the height using the midpoint value of each interval. The speaker provides formulas for each sum and explains how to apply them. The process is illustrated with a visual representation of the function and the rectangles, emphasizing the importance of understanding the steps involved in each type of Riemann sum.
Mindmap
Keywords
💡Riemann Sums
💡Function
💡Interval
💡Rectangles
💡Endpoint
💡Delta X (Δx)
💡Left Riemann Sum
💡Right Riemann Sum
💡Midpoint Riemann Sum
💡Summation
💡Notation
Highlights
The video explains the formulas for left, right, and midpoint Riemann sums and their conceptual understanding.
Riemann sums are used to approximate the area under a curve using rectangles with equal width.
The height of each rectangle is determined by the function value at the endpoints or midpoints.
The width of each rectangle is calculated as (B - A) / n, where A and B are the interval endpoints and n is the number of rectangles.
For the left Riemann sum, the height of each rectangle is the function value at the left endpoint.
For the right Riemann sum, the height of each rectangle is the function value at the right endpoint.
For the midpoint Riemann sum, the height of each rectangle is the function value at the midpoint of the interval.
The midpoint is calculated as the average of the left and right endpoints.
The area of each rectangle is found by multiplying the height (function value) by the width (Delta X).
The total area under the curve is approximated by summing the areas of all the rectangles.
The formulas for left, right, and midpoint sums have similar structures but use different endpoints or midpoints.
The left sum starts summing from i=0 to n-1, using the left endpoint of each interval.
The right sum starts summing from i=1 to n, using the right endpoint of each interval.
The midpoint sum starts summing from i=1 to n, using the midpoint of each interval.
The video provides a step-by-step explanation of how the formulas are derived and what they represent.
Understanding the conceptual meaning behind the formulas is emphasized over just memorizing them.
The video includes a visual example to illustrate the process of calculating Riemann sums.
The video serves as a helpful reference for understanding why the formulas look the way they do.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: