Over- and under-estimation of Riemann sums | AP Calculus AB | Khan Academy

Khan Academy

27 Sept 201704:01

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the concept of left and right Riemann sums as methods to approximate the area under a curve. It explains that for a strictly decreasing function over an interval, the left Riemann sum will overestimate the area, while the right Riemann sum will underestimate it. This is due to the heights used for the approximating rectangles being higher at the left edges and lower at the right edges of the subdivisions. The script also mentions that for strictly increasing functions, the roles would be reversed, and for other functions, the estimate could vary depending on the subdivision chosen.

Takeaways

📈 The left and right Riemann sums are methods to approximate the area under a curve.
🔍 For the left Riemann sum, the function is evaluated at the left endpoint of each subdivision.
📊 When approximating with the left Riemann sum, if the function is strictly decreasing, the result tends to be an overestimation.
📐 The right Riemann sum uses the right endpoint of each subdivision to determine the height of the approximating rectangles.
🔼 In the case of a strictly decreasing function, the right Riemann sum will generally lead to an underestimate of the area.
🔄 The choice of subdivisions can impact whether the approximation is an overestimation or an underestimate.
🔄 For a strictly increasing function, the roles of overestimation and underestimate switch between the left and right Riemann sums.
🤔 The accuracy of Riemann sums depends on the behavior of the function and the choice of subdivision points.
📊 Riemann sums provide a way to calculate areas when the function or the exact shape of the area is not easily defined.
🌟 Both left and right Riemann sums are valuable tools in numerical analysis for approximating integrals.
📈 Understanding the function's behavior is crucial for selecting the appropriate Riemann sum method for accurate approximations.

Q & A

What are the left and right Riemann sums used for in the context of the script?
-The left and right Riemann sums are used to approximate the area under a curve, specifically y equals g(x), between x equals two and x equals eight in the script.
How many subdivisions were chosen for the approximation in the example given?
-In the example provided, three equal subdivisions were chosen for the approximation.
What is the interval for the first subdivision in the left Riemann sum?
-The interval for the first subdivision in the left Riemann sum is from x equals two to x equals four.
Which function values are used to determine the height of the approximating rectangles in the left Riemann sum?
-The function values at the left endpoint of each subdivision, g(x), are used to determine the height of the approximating rectangles in the left Riemann sum.
Why does the left Riemann sum result in an overestimation for a strictly decreasing function?
-The left Riemann sum results in an overestimation for a strictly decreasing function because the rectangles have surplus area and are always larger than the actual area they are trying to approximate.
How does the right Riemann sum differ from the left Riemann sum in terms of estimation?
-The right Riemann sum tends to be an underestimate as it captures less area than it is trying to approximate, especially when dealing with a strictly decreasing function.
What is the interval for the second subdivision in the right Riemann sum?
-The interval for the second subdivision in the right Riemann sum is from x equals four to x equals six.
Which function values are used to determine the height of the approximating rectangles in the right Riemann sum?
-The function values at the right endpoint of each subdivision, g(x), are used to determine the height of the approximating rectangles in the right Riemann sum.
Why does the right Riemann sum result in an underestimation for a strictly decreasing function?
-The right Riemann sum results in an underestimation for a strictly decreasing function because the right endpoint values of g(x) are the lowest within each subdivision, leading to a lower height for the approximating rectangles.
How do the Riemann sums change if the function is strictly increasing instead of decreasing?
-If the function is strictly increasing, the roles of the left and right Riemann sums are swapped, with the left sum tending to be an underestimate and the right sum tending to be an overestimate.
What can affect whether the Riemann sum is an overestimate or an underestimate for functions that are neither strictly increasing nor decreasing?
-For functions that are neither strictly increasing nor decreasing, the type of subdivisions chosen can affect whether the Riemann sum results in an overestimate or an underestimate.

Outlines

00:00

📊 Understanding Left and Right Riemann Sums

This paragraph discusses the concept of left and right Riemann sums and how they are used to approximate the area under a curve. It explains that the choice of subdivisions and the points on the curve used for estimation can lead to overestimations or underestimations. The narrator uses the function g(x) as an example and describes how a left Riemann sum overestimates the area when the function is strictly decreasing, as the rectangles constructed will have surplus area not part of the actual area of interest. Conversely, a right Riemann sum underestimates the area for the same reason, as the rectangles do not capture the entire area of interest. The paragraph emphasizes the impact of the function's behavior (increasing or decreasing) on the accuracy of these approximations.

Mindmap

Keywords

💡Riemann Sums

Riemann sums are a mathematical technique used to approximate the area under a curve, which represents the definite integral of a function. In the context of the video, both left and right Riemann sums are discussed as methods to approximate this area. The video explains that these sums involve dividing the interval under consideration into smaller subintervals and using the values of the function at specific points within each subinterval to estimate the area. The left Riemann sum uses the left endpoint of each subinterval, while the right Riemann sum uses the right endpoint. The choice between these two methods depends on whether the function is increasing or decreasing within the interval.

💡Approximation

Approximation in mathematics refers to the process of estimating a value or quantity that is not exactly known. In the video, approximation is the central theme as it discusses how to estimate the area under a curve using Riemann sums. The video explains that approximations can be either overestimations or underestimations, depending on the method used and the behavior of the function within the interval. The concept is crucial for understanding numerical analysis and the practical application of integral calculus.

💡Subdivisions

Subdivisions refer to the partitioning of an interval into smaller segments. In the context of the video, subdivisions are created when calculating Riemann sums to approximate the area under a curve. The video describes how the interval from x equals two to x equals eight is divided into three equal subdivisions for the purpose of approximation. Each subdivision is then used to calculate the height of rectangles that approximate the area under the curve.

💡Left Riemann Sum

The left Riemann sum is a specific method of approximating the area under a curve by using the left endpoint of each subdivision to determine the height of the approximating rectangles. In the video, it is explained that when the function is strictly decreasing over the interval, the left Riemann sum will result in an overestimation of the actual area. This is because the value of the function at the left endpoint will be higher than the average value within the subdivision, leading to taller rectangles and a larger estimated area.

💡Right Riemann Sum

The right Riemann sum is the counterpart to the left Riemann sum, where instead of using the left endpoint, the right endpoint of each subdivision is used to determine the height of the approximating rectangles. As discussed in the video, when dealing with a strictly decreasing function, the right Riemann sum will result in an underestimation of the area under the curve. This occurs because the right endpoint will yield the lowest value of the function within the subdivision, thus creating shorter rectangles and a smaller estimated area.

💡Decreasing Function

A decreasing function is one where the value of the function decreases as the independent variable (often x) increases. In the video, the behavior of the function as strictly decreasing is crucial in determining whether the left or right Riemann sum will result in an overestimation or underestimation. The video explains that for a strictly decreasing function, the left Riemann sum will overestimate the area because the function's value at the left endpoint is higher, while the right Riemann sum will underestimate the area due to the lower function value at the right endpoint.

💡Overestimation

Overestimation is the act of estimating a value to be larger than its actual value. In the context of the video, overestimation occurs when using the left Riemann sum for a strictly decreasing function. The video illustrates that the rectangles formed by the left Riemann sum have surplus area beyond the actual area under the curve, leading to an overestimation of the integral. This is due to the higher function values at the left endpoints compared to the rest of the subdivision.

💡Underestimation

Underestimation is the act of estimating a value to be smaller than its actual value. In the video, underestimation is discussed in relation to the right Riemann sum for a strictly decreasing function. The video shows that the right Riemann sum fails to capture the entire area under the curve, resulting in an underestimate. This happens because the rectangles formed using the right endpoints have a lower function value, leading to shorter rectangles and a smaller estimated area than the actual.

💡Area Under a Curve

The area under a curve is a fundamental concept in calculus, representing the definite integral of a function over a specified interval. In the video, the area under the curve y = g(x) between x = 2 and x = 8 is the quantity being approximated using Riemann sums. The video explains that this area can be approximated by dividing the interval into subdivisions and using rectangles to estimate the area. The accuracy of this approximation depends on the method of Riemann sums used and the behavior of the function within the interval.

💡Strictly Decreasing

A strictly decreasing function is one where the derivative is negative for all values in the interval under consideration, meaning the function never increases and is always getting smaller as the independent variable increases. In the video, the concept of a strictly decreasing function is important because it dictates which Riemann sum method will result in an overestimation or underestimation. For a strictly decreasing function, the left Riemann sum will overestimate and the right Riemann sum will underestimate the area under the curve.

💡Endpoints

Endpoints refer to the starting and ending points of an interval. In the context of the video, the endpoints are the values of the independent variable (x) that define the interval over which the area under the curve is being approximated. The video discusses how the choice between left and right Riemann sums is directly related to the endpoints of the subdivisions created within the interval. The left endpoint is used for the left Riemann sum, and the right endpoint is used for the right Riemann sum to estimate the area under the curve.

Highlights

The discussion focuses on approximating the area under a curve using left and right Riemann sums.

The left Riemann sum involves dividing the interval into equal subdivisions and using the left side of each to estimate the height of rectangles.

The right Riemann sum uses the right side of each subdivision to define the height of the rectangles for approximation.

For a strictly decreasing function over an interval, the left Riemann sum will overestimate the area.

The right Riemann sum will underestimate the area for the same function and interval as the left Riemann sum.

The left Riemann sum's overestimation is due to the surplus area of the rectangles used for approximation.

The right Riemann sum's underestimation is because it does not capture the entire area of the function's curve within the rectangles.

The value of the function at the left edge is higher than any point within the subdivision for a strictly decreasing function.

The right Riemann sum uses the lowest value of the function within a subdivision, leading to a lower height for the approximating rectangles.

For a strictly increasing function, the behaviors of the left and right Riemann sums would be reversed.

The type of subdivisions chosen can influence whether an approximation is an overestimate or an underestimate.

The transcript provides a clear visualization and explanation of the concepts of left and right Riemann sums.

The mathematical concepts are explained in a manner accessible to those who may not be deeply familiar with calculus.

The transcript serves as an educational resource for understanding Riemann sums and their applications in approximating areas under curves.

The transcript offers insights into the relationship between the behavior of a function and the accuracy of Riemann sum approximations.

The approximation process is contextualized with a practical example, enhancing the understanding of the theoretical concepts.

Transcripts

Browse More Related Video

Worked example: over- and under-estimation of Riemann sums | AP Calculus AB | Khan Academy

Left, Right, & Midpoint Riemann Sum Formulas

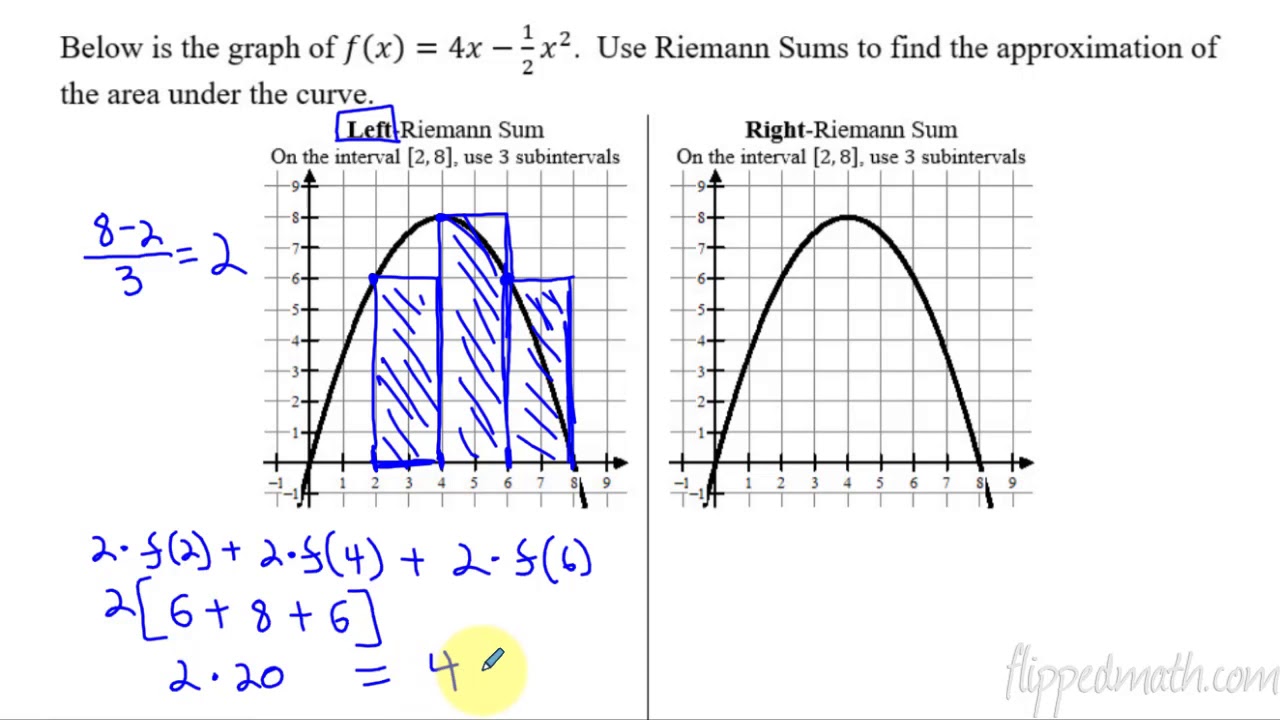
Calculus AB/BC – 6.2 Approximating Areas with Riemann Sums

Worked example: finding a Riemann sum using a table | AP Calculus AB | Khan Academy

Business Calculus - Math 1329 - Section 5.3 - The Definite Integral and Fundamental Thm of Calculus

AP Calculus AB: Lesson 6.2 Riemann and Trapezoidal Sums

Over- and under-estimation of Riemann sums | AP Calculus AB | Khan Academy

Takeaways

Q & A

What are the left and right Riemann sums used for in the context of the script?

How many subdivisions were chosen for the approximation in the example given?

What is the interval for the first subdivision in the left Riemann sum?

Which function values are used to determine the height of the approximating rectangles in the left Riemann sum?

Why does the left Riemann sum result in an overestimation for a strictly decreasing function?

How does the right Riemann sum differ from the left Riemann sum in terms of estimation?

What is the interval for the second subdivision in the right Riemann sum?

Which function values are used to determine the height of the approximating rectangles in the right Riemann sum?

Why does the right Riemann sum result in an underestimation for a strictly decreasing function?

How do the Riemann sums change if the function is strictly increasing instead of decreasing?

What can affect whether the Riemann sum is an overestimate or an underestimate for functions that are neither strictly increasing nor decreasing?