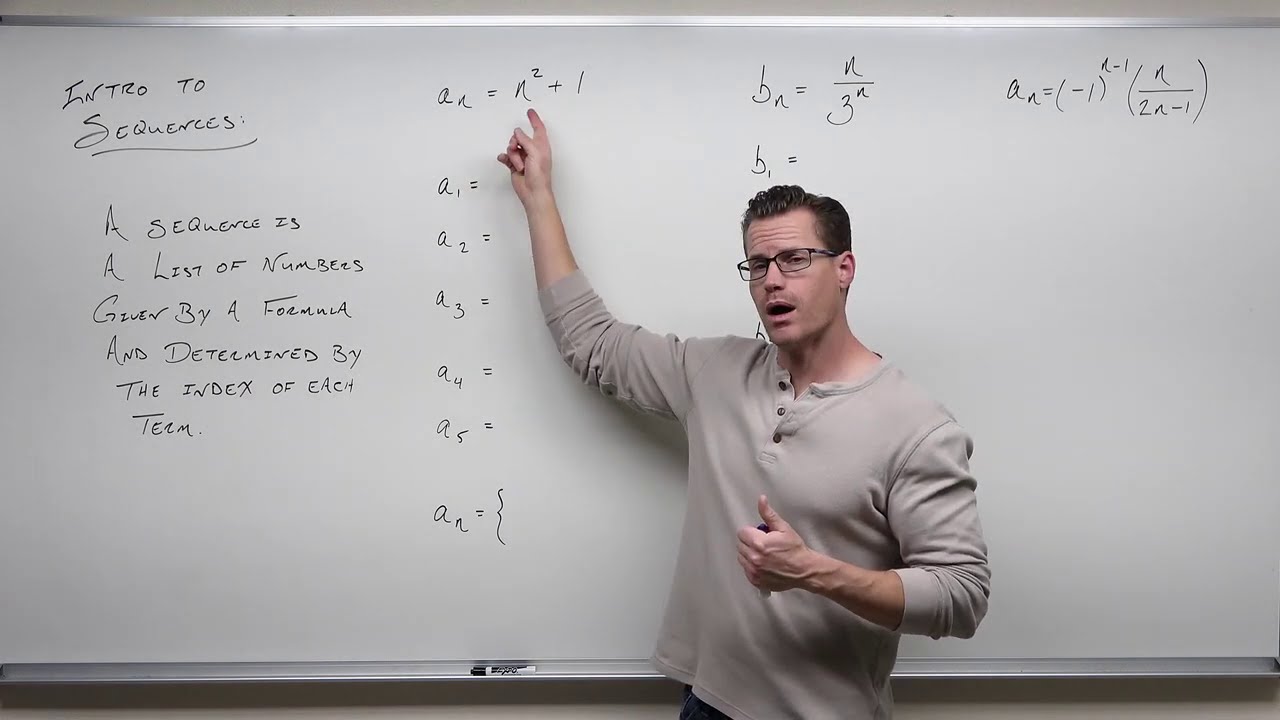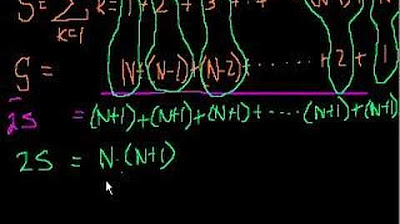Introduction to Series and Summation Notation (Precalculus - College Algebra 68)

Professor Leonard

17 Nov 202042:41

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers an in-depth exploration of series and sequences, two fundamental concepts in mathematics. The presenter clarifies that a series is essentially the sum of the terms of a sequence, and introduces the concept of series notation, denoted by the Greek letter sigma (Σ), which signifies the addition of terms. The script delves into the intricacies of series, including how to calculate their sum efficiently using various formulas, which are applicable to different types of series such as arithmetic and geometric progressions. The presenter also highlights the importance of understanding series for their applications in calculus and the manipulation of transcendental numbers like pi and e. The video script guides viewers through the process of finding the sum of a series without manually adding each term by leveraging mathematical induction and specific formulas for different series types. It concludes with an example that illustrates how to manipulate a series to fit the formulas, even when the series does not start at the conventional index of one. The summary underscores the script's aim to demystify series and sequences, making them accessible and engaging for viewers.

Takeaways

📚 A series is the sum of the terms of a sequence, which can be represented mathematically using the Greek letter sigma (Σ).
🔢 Series can be manipulated and calculated using various formulas, which simplify the process of finding the sum of the terms without manual addition.
🔁 The concept of sequences and series is fundamental to understanding more complex mathematical concepts, including calculus.
🌟 Special cases of series, such as geometric series, have unique properties that allow for the summation of an infinite number of terms.
📈 Series can be used to represent and work with transcendental numbers like pi (π) and e in a series form.
🤔 Understanding how to work backwards from a series to reconstruct the original sequence is an important skill, which involves identifying patterns and relationships between terms.
🔢 The formulas for summing series are derived from patterns and are proven using mathematical induction, a common method in mathematical proof.
📌 When a series is based on a sequence with a constant term, the sum can be found by multiplying the constant by the number of terms.
➕ Addition and subtraction are commutative and associative, allowing for the separation of a series into smaller, manageable parts that can be added back together.
🚫 It's crucial to maintain the correct starting and ending points when manipulating a series to avoid errors.
🧮 For series that do not start at the first term, the approach involves taking the full series from the start and subtracting the terms that are not required.

Q & A

What is the main difference between a sequence and a series?
-A sequence is a list of numbers, whereas a series is the sum of the terms of a sequence. A series adds up the terms, whereas a sequence does not necessarily involve addition.
What is the symbol used to represent the sum in a series and what does it stand for?
-The symbol used to represent the sum in a series is the Greek letter 'sigma' (Σ), which stands for 'sum'.
How does one prove formulas related to series mathematically?
-One common method to prove formulas related to series is by using mathematical induction, which is a technique that will be covered in later videos.
What are some special cases where an infinite series can converge?
-Some special cases where an infinite series can converge include geometric series with a common ratio between -1 and 1, excluding -1 and 1 themselves.
How does the concept of a series relate to calculus?
-In calculus, particularly in Calculus 2, series are used to perform operations on functions, including finding areas under curves and volumes of revolution, by summing an infinite number of terms.
What are the formulas used to calculate the sum of a series for the sequences based on k, k squared, and k cubed?
-For a sequence based on k, the formula is (n * (n + 1)) / 2. For k squared, it is (n * (n + 1) * (2n + 1)) / 6. For k cubed, it is ((n * (n + 1) / 2) ^ 2).
How can you represent a series with a starting index other than 1?
-If a series does not start at 1, you can represent it by taking the whole series that starts at 1 and subtracting the terms from 1 up to, but not including, the starting index of your series.
What is the significance of the variable 'k' in a series?
-The variable 'k' is the index of the series and it is used to denote the position of each term within the series. It is crucial for identifying the starting and ending points of the series.
How can you manipulate a series to make it match the form required by the formulas for easy summation?
-You can manipulate a series by separating it into smaller series based on addition and subtraction, factoring out constants, and ensuring that each smaller series matches the form of the formulas provided.
What is the process of converting a series into a sequence?
-The process involves listing the terms of the series, making them all the same form, identifying the unchanging elements, and relating the changing elements back to the index 'k' of the series.
Why is it important to use different variables for the series and the sequence it is based on?
-Different variables are important to avoid ambiguity and to clearly distinguish between the sequence (based on 'k') and the nth term of the series (based on 'n'). This allows for accurate representation and manipulation of the series.
How can you find the sum of a constant series without actually adding each term?
-For a constant series, you can multiply the constant by the number of terms in the series (n). This is because repeated addition of the same number is equivalent to multiplication.

Outlines

00:00

😀 Understanding Series Through Sequences

The video introduces the concept of series as a continuation of sequences. It explains that a series is the sum of the terms of a sequence, contrasting it with sequences that are merely lists of numbers. The importance of understanding series is emphasized, particularly for their role in calculus. The video outlines the basic formula for a series, using the Greek letter sigma to represent the sum, and demonstrates how to find the sum of the first n terms of a series.

05:01

🔢 Series Summation and Proof by Induction

The paragraph delves into the process of summing a series and how it can be proven using mathematical induction. It also touches on the concept of odd numbers in sequences and how they can be represented in different ways. The content emphasizes the manipulability of series by altering start and end points, which can change the resulting sequence.

10:02

🔁 Building a Series From a Sum

This section discusses the reverse process of creating a series from a given sum. It involves listing terms, identifying patterns, and expressing the series in a standardized form. The paragraph also explains the need for different indices for the series and the sequence it's based on, highlighting the technique to determine the stopping point of a series.

15:02

📝 Series Representation and Formulas

The video script explains how to represent a series in notation and the importance of using different variables for clarity. It introduces formulas that allow for the quick summation of series terms without extensive calculation. The paragraph emphasizes that these formulas are applicable for both finite and infinite series, subject to certain conditions.

20:03

🧮 Summing Series with Formulas

The paragraph focuses on the practical application of formulas to sum series quickly. It provides examples of how to use these formulas for different types of series, including those based on k, k squared, and k cubed. The importance of knowing the endpoint of a series for these formulas to work is highlighted.

25:05

🔗 Series Separability and Constant Multiplication

This section explains the properties of addition and subtraction that allow for the separation of a series into smaller, more manageable parts. It also addresses the concept of factoring out constants from a series and the multiplication of constants within the series. The video aims to clarify the process of simplifying series for easier summation using the established formulas.

30:06

🔍 Manipulating Series to Match Formulas

The final paragraph demonstrates how to manipulate a series that does not start at the conventional beginning to fit the formulas provided. It shows how to adjust the series by subtracting unnecessary terms and ensuring the starting point aligns with the formulas. The paragraph reinforces the idea that sequences and series are manageable with the right approach and formulas.

Mindmap

Keywords

💡Series

A series in mathematics is the sum of the terms of a sequence. It is a fundamental concept in calculus and is used to represent the total obtained when adding together all elements in an arithmetic or geometric progression. In the video, series are explored in depth, showing how they are built from sequences and how they can be manipulated mathematically to find their sums using various formulas.

💡Sequence

A sequence is an ordered list of numbers or terms. It provides the individual elements that are then summed to form a series. The video discusses how a series is derived from a sequence, emphasizing the importance of understanding sequences as a prerequisite to grasping series.

💡Convergence

Convergence in the context of series refers to the approach of the sum of an infinite sequence towards a finite limit. The video touches on this concept when discussing the special properties of certain series, like geometric series, which can converge under specific conditions.

💡Divergence

Divergence is the opposite of convergence. It describes a situation where the sum of an infinite series does not approach a finite value but instead increases without bound. The video mentions this in contrast to convergence when discussing the behavior of series.

💡Sigma Notation

Sigma notation (∑) is a mathematical symbol used to represent the sum of all terms in a series. It is a compact way of expressing the addition of the terms of a sequence. The video explains how sigma notation is used to denote both the start and end points of a series and how it is central to performing calculations with series.

💡Induction

Induction is a mathematical proof technique used to establish that a given statement holds for all positive integers. The video script mentions that many of the formulas and properties of series are proven by induction, which is a way to show that a pattern holds for the first element and then that if it holds for one element, it holds for the next.

💡Geometric Series

A geometric series is a type of series where each term is found by multiplying the previous term by a fixed, non-zero number called the common ratio. The video discusses geometric series as an example of a series that can converge under the condition that the common ratio is between -1 and 1.

💡Transcendental Numbers

Transcendental numbers are numbers that are not algebraic, meaning they are not roots of any non-zero polynomial equation with rational coefficients. The video references transcendental numbers like pi (π) and e when discussing how series can be used to represent and work with these special types of numbers.

💡Summation Formulas

Summation formulas are mathematical formulas used to find the sum of a series without having to add each term individually. The video provides several examples of these formulas for different types of series, such as arithmetic and geometric series, and explains how they simplify the process of finding the sum of a series.

💡Alternating Series

An alternating series is a series in which the signs of the terms alternate between positive and negative. The video discusses how the sign of the terms in a series can change, and it provides an example of a series where the terms alternate between being positive and negative.

💡Factorial

Factorial, denoted by 'n!', is the product of all positive integers less than or equal to n. It is used in the formulas for the sum of series involving powers of k, such as k squared or k cubed. The video uses the concept of factorial in the context of summation formulas for series.

Highlights

A series adds up the terms of a sequence, which can be manipulated with predictable formulas for easier computation.

Series can be proven by induction, a method to be introduced in later videos.

Infinite series can converge to a value, a concept explored in calculus.

The Greek letter sigma (Σ) represents the sum in a series.

Series are built from a sequence, starting at a certain index and ending at another, which can be finite or infinite.

The formula for the sum of the first n natural numbers is n*(n+1)/2.

For sequences based on k squared or k cubed, there are specific formulas to find the sum of the series.

Series can be manipulated by altering the starting and ending points, which can change the sequence being worked with.

Odd numbers can be defined in two different ways using series, starting from zero or one.

Transcendental numbers like pi and e can be represented in a series form.

Series can be built backwards from a sum by identifying a pattern and expressing it in terms of an index.

The sum of a constant series is simply the constant multiplied by the number of terms.

Series can be separated by addition and subtraction, and constants can be factored out.

The sum of a series can be found without listing all the terms by applying the appropriate formula.

When a series does not start at one, it can be adjusted by subtracting the terms from the series that starts at one up to the desired starting point.

Arithmetic and geometric sequences and series will be discussed in upcoming videos, along with proof by induction.

Transcripts

Browse More Related Video

Sequence and Series | Terms of Sequence and Associated Series | Pre-Calculus

Introduction to Sequences (Precalculus - College Algebra 67)

Geometric Series (Precalculus - College Algebra 72)

Arithmetic Sequences (Precalculus - College Algebra 69)

Sequences and Series (part 1)

Ch. 12.3 Geometric Sequences

Related Tags

Series Calculation Sequences Mathematics Formulas Induction Proof Educational Content Calculus Transcendental Numbers Series Manipulation Constant Series Arithmetic Sequences Geometric Series