So how does your computer ACTUALLY compute sine? Basics of trig and more…
TLDRThe video script offers an insightful exploration into trigonometric functions, starting with the traditional right-angled triangle approach and moving on to a circle with a radius of 1 to visualize sine, cosine, and tangent in a more intuitive way. It explains how angles can be measured in radians, derived from the circumference of a circle, and how these measurements lead to the oscillation of trigonometric functions as the angle varies. The script delves into the concept of the dot product, illustrating its connection to cosine and its role in projecting one vector onto another. It also discusses the practical implementations of trigonometric functions in computing, including historical approximations, lookup tables, and modern computational techniques like range reduction and polynomial approximations. The video concludes with a teaser for an upcoming math course focused on making complex mathematical concepts more accessible, particularly for game development.
Takeaways
- 📐 **Trigonometric Functions**: They are typically taught using a right-angled triangle with sides labeled opposite, adjacent, and hypotenuse, and angles represented by Greek letters like theta.
- 📈 **Sine, Cosine, and Tangent**: These are the primary trigonometric functions defined as sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent).
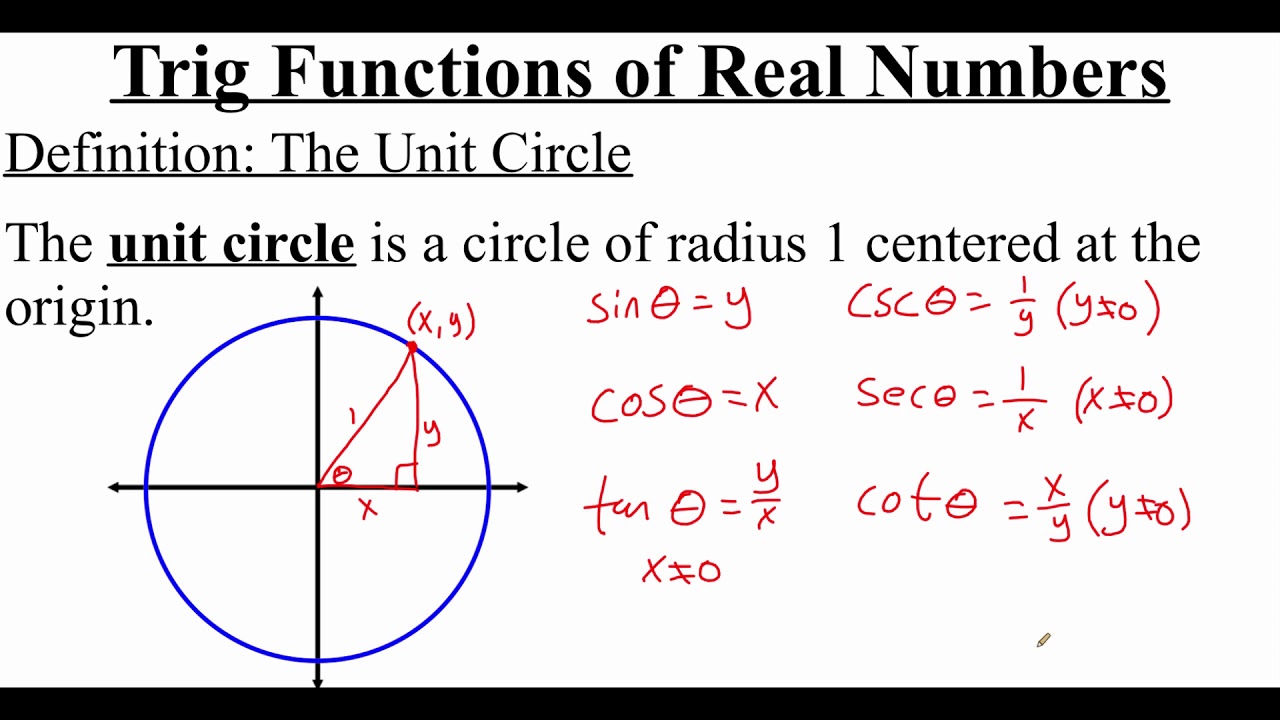
- 🔄 **Unit Circle**: An alternative visualization of trigonometric functions uses a circle with a radius of 1, where any point on the circle is at a unit distance from the center.
- 📏 **Radians vs. Degrees**: Angles can be expressed in radians, which are based on the distance along the circle's circumference, as opposed to degrees which are an arbitrary system.
- 🌀 **Graphs of Trigonometric Functions**: The graphs of sine and cosine oscillate between 1 and -1, and tangent is undefined at certain points (PI/2 and -PI/2), causing it to 'freak out' on the graph.
- 🔺 **Vector Representation**: The x-component of a vector on the unit circle corresponds to the cosine of the angle, which can be mathematically represented as the dot product of the vector with the x-axis vector.
- 📉 **Dot Product**: The dot product of two unit vectors equals the cosine of the angle between them, which is also the horizontal distance from the tip of one vector to the x-axis if the other vector is aligned with the x-axis.
- 💾 **Lookup Tables**: In the past, lookup tables were used to approximate trigonometric function values by precomputing and interpolating between stored values.
- 🔍 **Taylor Series**: A mathematical tool that can be used to approximate trigonometric functions, though it has non-uniform error scaling away from 0.
- 🔧 **Range Reduction**: An approach to computing trigonometric functions that involves mapping input values to a reduced range where the function can be more easily approximated.
- ⚙️ **Hardware Implementation**: Modern hardware and libraries often use a combination of range reduction, polynomial approximation, and reconstruction to compute trigonometric function values efficiently.
- 📚 **Further Resources**: Detailed explanations and implementations of trigonometric functions can be found in historical mathematical works, Intel papers, GNU C libraries, and various educational blogs and courses.
Q & A
What are the three primary trigonometric functions in relation to a right-angled triangle?
-The three primary trigonometric functions are sine (sin), cosine (cos), and tangent (tan). They are defined as follows: sin is the ratio of the length of the side opposite the angle theta to the length of the hypotenuse, cos is the ratio of the length of the adjacent side to the length of the hypotenuse, and tan is the ratio of the length of the side opposite the angle theta to the length of the adjacent side.
How is the concept of a unit circle used to understand trigonometric functions?
-A unit circle is a circle with a radius of exactly 1. It helps in visualizing trigonometric functions by placing any point on the circle at a distance of exactly 1 from the center. The coordinates of this point can be used to define the sine and cosine of the angle theta, where the y-coordinate corresponds to sin(theta) and the x-coordinate corresponds to cos(theta).
Why are radians used instead of degrees to measure angles in trigonometry?
-Radians are used because they provide a more natural measure that is directly related to the arc length. One full revolution around a circle is 2π radians, which corresponds to the circumference of the circle with radius 1. This is more intuitive than 360 degrees, which is an arbitrary system leftover from historical practices.
What happens to the values of sin(theta), cos(theta), and tan(theta) as the point on the unit circle rotates?
-As the point rotates around the unit circle, the values of sin(theta) and cos(theta) oscillate between 1 and -1, while tan(theta) oscillates between positive and negative infinity, with the exception of undefined values at π/2 and -π/2, where the tangent function has vertical asymptotes.
How is the dot product related to the cosine of an angle?
-The dot product of two vectors can be used to find the cosine of the angle between them. Specifically, if two unit vectors are given, the dot product of these vectors is equal to the cosine of the angle between them. This is because the dot product calculates the product of the x-components and y-components of the vectors, which corresponds to the horizontal and vertical distances in the unit circle model.
What is a common method for approximating trigonometric functions in computer programming?
-A common method for approximating trigonometric functions in computer programming includes using a combination of range reduction, polynomial approximation (like Taylor series or minimax approximation), and a reconstruction step to map the computed value back into the appropriate quadrant.
Why are lookup tables not as commonly used in modern computing for trigonometric function approximation?
-Lookup tables are not as commonly used in modern computing due to the slowness of cache misses and the advancements in approximation algorithms that can provide similar or better accuracy with less memory and computational overhead.
What is the significance of the Taylor series in approximating trigonometric functions?
-The Taylor series is a mathematical tool that can be used to approximate functions around a given point. In the context of trigonometric functions, it provides a way to represent these functions as an infinite sum of terms calculated from the function's derivatives at a single point, typically zero. However, it has the drawback of non-uniform error scaling, with larger errors further away from the point of expansion.
What is the role of range reduction in the computation of trigonometric functions?
-Range reduction is a technique used to limit the input domain of a function to a smaller range, which can then be approximated more accurately and efficiently. For trigonometric functions, it involves mapping any given angle to a smaller equivalent angle within a specific range, often [0, π/2] for sine and cosine, allowing for more precise and uniform approximation.
How does the symmetry of the sine wave simplify the approximation process?
-The symmetry of the sine wave allows for the simplification of the approximation process by recognizing that the function repeats every 2π radians (or 360 degrees) and is symmetric about the origin. This means that only a quarter of the wave needs to be approximated, with the rest of the wave being derived through reflection and inversion based on this fundamental period.
What is the historical context behind the approximation methods for trigonometric functions?
-Historically, various approximation methods have been developed to calculate trigonometric functions. For instance, the Indian mathematician Bhaskara provided a formula in the 7th century that worked well for angles in the range of [0, π] with a small absolute error. These historical methods laid the foundation for more advanced and efficient approximation techniques used in modern computing.
How can one find more intuitive explanations of trigonometry and related mathematical concepts for game development?
-For more intuitive explanations of trigonometry, matrices, and other mathematical concepts relevant to game development, one can look for educational resources such as upcoming math courses, blogs, and papers from institutions or individuals specializing in these areas. The script mentions an upcoming math course and a blog by Robin Green, which are linked in the description for further exploration.
Outlines
📐 Understanding Trigonometric Functions Through Unit Circle
The first paragraph introduces trigonometric functions using a unit circle, where any point on the circle is at a distance of exactly 1 from the center. It explains that angles are typically measured in degrees from 0 to 360, but an alternative unit called radians is based on the circumference of the circle, which is 2π radians for a unit circle. The trigonometric functions sine, cosine, and tangent are visualized in terms of distances from a point on the circle to the axes. The paragraph also discusses how these functions change as the point moves around the circle and how they can be graphed. The concept of the dot product is introduced as a mathematical way to express the cosine function, and its relevance to the scalar projection of one vector onto another is highlighted. Lastly, the paragraph touches on historical approximations and modern computational methods for these functions, including lookup tables and polynomial approximations like Taylor series.
🔍 Advanced Computation of Trigonometric Functions
The second paragraph delves into the computational techniques for trigonometric functions, noting that direct computation using Taylor series can be problematic due to non-uniform error. It discusses the concept of range reduction, where the function's period is exploited to limit the approximation to a small segment of its cycle. This is followed by an approximation step, which might use a polynomial like the Taylor series or a minimax approximation, and a final reconstruction step to map the computed value back into the correct quadrant. The paragraph mentions that industry practices have evolved from using lookup tables to more sophisticated methods due to the slowness of cache misses. It also references resources such as an Intel paper and the GNU C library for further reading, and it teases an upcoming math course focused on intuitive explanations of trigonometry and related topics for game development.
Mindmap
Keywords
💡Trigonometric functions
💡Right-angled triangle
💡Unit circle
💡Degrees and radians
💡Sine (sin)
💡Cosine (cos)
💡Tangent (tan)
💡Dot product
💡Vector
💡Taylor series
💡Range reduction
💡Lookup table
Highlights
Trigonometric functions are introduced using a right-angled triangle with an angle typically called theta.
The sides of the triangle are labeled as opposite, adjacent, and hypotenuse, with sine, cosine, and tangent defined accordingly.
An alternative visualization of trigonometric functions is presented through a unit circle with a radius of 1.
Angles are expressed in radians, which are derived from the circumference of a circle with a radius of 1.
The sine and cosine of an angle are defined as the vertical and horizontal distances from the circle's point to the origin.
Tangent is the ratio of the opposite side to the adjacent side and is visualized as the distance from the intersection of extended lines to the x-axis.
The values of sin theta, cos theta, and tan theta change as the point moves around the circle, with sin and cos oscillating between 1 and -1.
Tangent is undefined at PI/2 and -PI/2 due to the division by zero, which is clarified through the graphical representation.
The x component of a unit circle vector is identified as the cosine of the angle, leading to the concept of the dot product.
The dot product of two unit vectors is shown to be equivalent to the cosine of the angle between them.
The dot product is used to calculate the scalar projection of one vector onto another, which is the horizontal distance.
Trigonometric functions are computed using various approximations, with historical methods like Bhaskara's formula mentioned.
Lookup tables were used in the past for game development to precompute values and interpolate for results, with a small error margin.
Taylor series expansion is a common method for computing trigonometric functions, but it has non-uniform error distribution.
Modern approaches to computing trigonometric functions involve range reduction, approximation, and reconstruction steps.
Symmetry in the sin wave allows for approximation of only a small portion of the wave, as the function repeats every 2 PI radians.
Polynomial approximations, such as Taylor series or minimax, are used to compute values within the reduced range.
Hardware and library functions for trigonometric calculations are implemented using these methods, with examples from Intel and the GNU C library.
An upcoming math course for game development will provide more intuitive explanations of trigonometry, matrices, and related mathematical concepts.
Transcripts
Browse More Related Video

Trig 0.2 - Trig Functions Defined on the Unit Circle

How to Use the Unit Circle in Trigonometry (Precalculus - Trigonometry 7)
4.3.4 Trigonometric Functions of Real Numbers

Trig - 0.6 Trig Functions of Acute Angles

Trigonometry: Unit Circle

Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6)
5.0 / 5 (0 votes)
Thanks for rating: